Regresi logaritmik di r (langkah demi langkah)
Regresi logaritmik adalah jenis regresi yang digunakan untuk memodelkan situasi di mana pertumbuhan atau penurunan pada awalnya meningkat dengan cepat dan kemudian melambat seiring berjalannya waktu.
Misalnya, grafik berikut menunjukkan contoh peluruhan logaritmik:

Untuk situasi seperti ini, hubungan antara variabel prediktor dan variabel respon dapat dimodelkan dengan baik menggunakan regresi logaritmik.
Persamaan model regresi logaritma berbentuk sebagai berikut:
y = a + b*ln(x)
Emas:
- y : variabel respon
- x: variabel prediktif
- a, b: koefisien regresi yang menggambarkan hubungan antara x dan y
Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi logaritmik di R.
Langkah 1: Buat datanya
Pertama, mari buat data palsu untuk dua variabel: x dan y :
x=1:15 y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)
Langkah 2: Visualisasikan datanya
Berikutnya, mari buat diagram sebar singkat untuk memvisualisasikan hubungan antara x dan y :
plot(x, y)
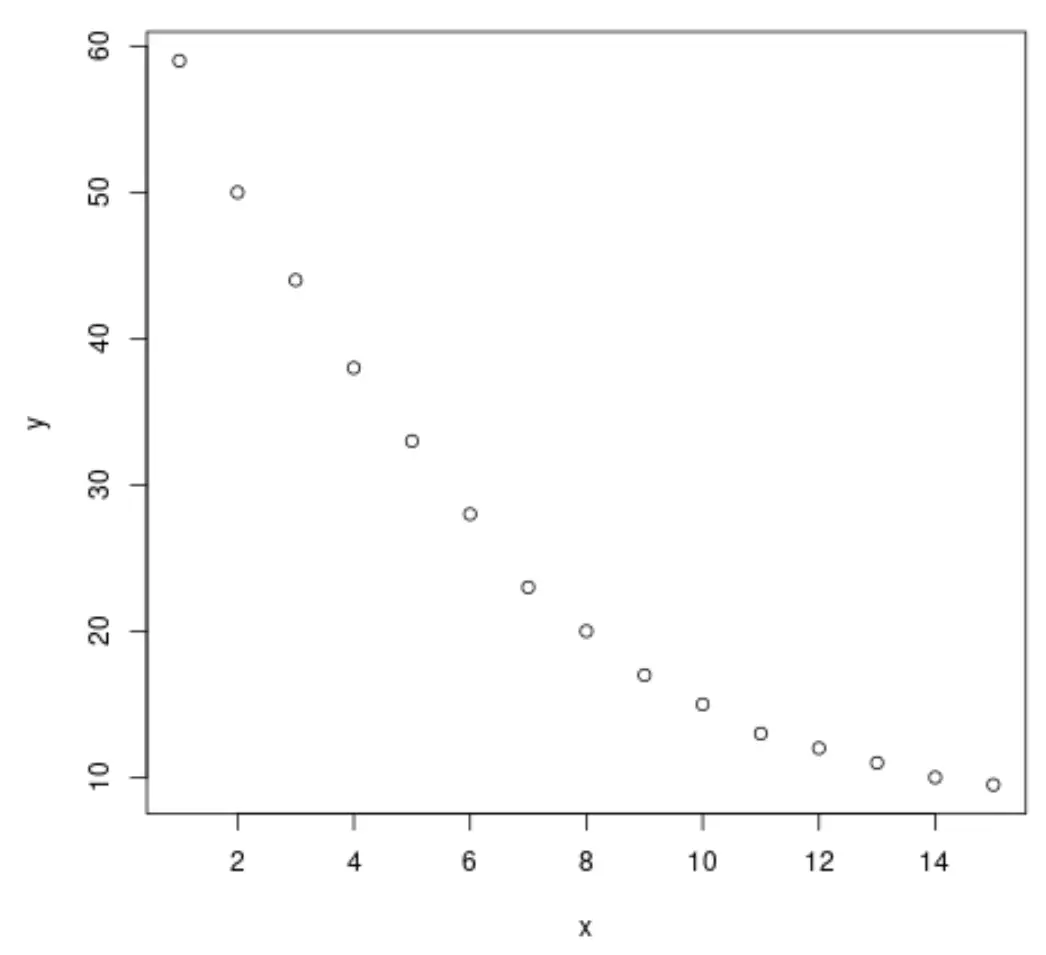
Dari grafik terlihat jelas adanya pola peluruhan logaritmik antara kedua variabel. Nilai variabel respon, y , menurun dengan cepat pada awalnya, kemudian melambat seiring berjalannya waktu.
Oleh karena itu, tampaknya bijaksana untuk menggunakan persamaan regresi logaritmik untuk menggambarkan hubungan antar variabel.
Langkah 3: Sesuaikan model regresi logaritma
Selanjutnya, kita akan menggunakan fungsi lm() untuk menyesuaikan model regresi logaritma, menggunakan logaritma natural x sebagai variabel prediktor dan y sebagai variabel respon.
#fit the model model <- lm(y ~ log (x)) #view the output of the model summary(model) Call: lm(formula = y ~ log(x)) Residuals: Min 1Q Median 3Q Max -4.069 -1.313 -0.260 1.127 3.122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 63.0686 1.4090 44.76 1.25e-15 *** log(x) -20.1987 0.7019 -28.78 3.70e-13 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.054 on 13 degrees of freedom Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13
Nilai F keseluruhan model adalah 828,2 dan nilai p yang sesuai sangat rendah (3,702e-13), menunjukkan bahwa model secara keseluruhan berguna.
Dengan menggunakan koefisien dari tabel keluaran, kita dapat melihat bahwa persamaan regresi logaritmik yang sesuai adalah:
kamu = 63,0686 – 20,1987 * ln(x)
Kita dapat menggunakan persamaan ini untuk memprediksi variabel respon y berdasarkan nilai variabel prediktor x . Misalnya, jika x = 12, maka kita prediksi y adalah 12.87 :
y = 63,0686 – 20,1987 * ln(12) = 12,87
Bonus: Jangan ragu untuk menggunakan kalkulator regresi logaritma online ini untuk secara otomatis menghitung persamaan regresi logaritma untuk variabel prediktor dan respons tertentu.
Langkah 4: Visualisasikan model regresi logaritma
Terakhir, kita dapat membuat grafik cepat untuk memvisualisasikan seberapa cocok model regresi logaritmik dengan data:
#plot x vs. y plot(x, y) #define x-values to use for regression line x=seq(from= 1 , to= 15 , length. out = 1000 ) #use the model to predict the y-values based on the x-values y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )), interval=" confidence ") #add the fitted regression line to the plot (lwd specifies the width of the line) matlines(x,y, lwd= 2 )
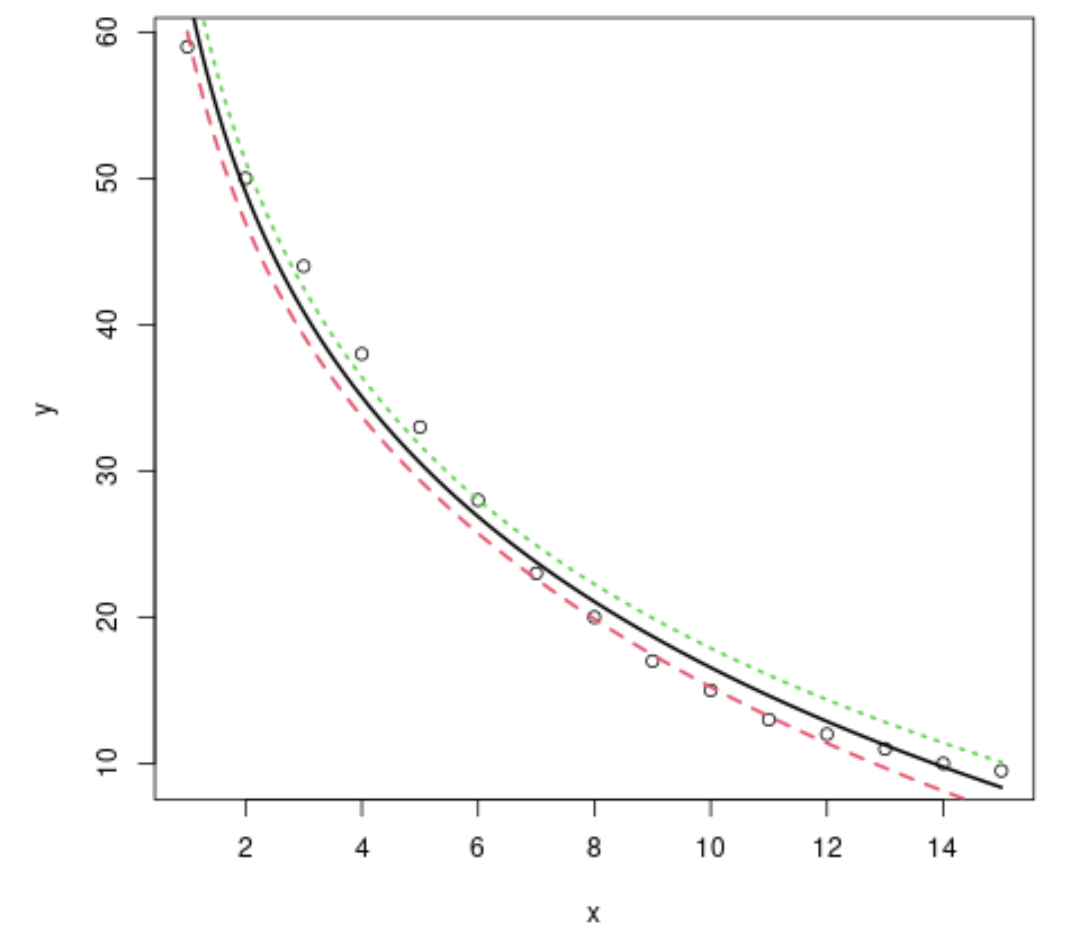
Kita dapat melihat bahwa model regresi logaritmik berfungsi dengan baik dalam menyesuaikan kumpulan data tertentu.
Sumber daya tambahan
Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi kuadrat di R
Bagaimana melakukan regresi eksponensial di R
Bagaimana melakukan regresi polinomial di R