Pengantar regresi logistik

Ketika kita ingin memahami hubungan antara satu atau lebih variabel prediktor dan variabel respon kontinu, kita sering menggunakan regresi linier .

Namun jika variabel respon bersifat kategorikal, kita dapat menggunakan regresi logistik .

Regresi logistik adalah jenis algoritme klasifikasi karena ia berupaya “mengklasifikasikan” observasi dalam kumpulan data ke dalam kategori berbeda.

Berikut beberapa contoh penggunaan regresi logistik:

• Kami ingin menggunakan skor kredit dan saldo bank untuk memprediksi apakah pelanggan tertentu akan gagal membayar pinjaman. (Variabel respons = “Default” atau “Tidak ada default”)
• Kami ingin menggunakan rata-rata rebound per game dan rata-rata poin per game untuk memprediksi apakah seorang pemain bola basket tertentu akan direkrut ke NBA atau tidak (Variabel respons = “Drafted” atau “Undrafted”).
• Kami ingin menggunakan luas persegi dan jumlah kamar mandi untuk memprediksi apakah sebuah rumah di kota tertentu akan dijual dengan harga $200.000 atau lebih. (Variabel respon = “Ya” atau “Tidak”)

Perhatikan bahwa variabel respon di masing-masing contoh ini hanya dapat mengambil satu dari dua nilai. Bandingkan dengan regresi linier yang variabel responnya bernilai kontinu.

Persamaan regresi logistik

Regresi logistik menggunakan metode yang disebut estimasi kemungkinan maksimum (detailnya tidak akan dibahas di sini) untuk mencari persamaan dengan bentuk berikut:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Emas:

• X _j : variabel prediktif ^ke -j
• β _j : estimasi koefisien variabel prediktif ke- ^j

Rumus di sisi kanan persamaan memprediksi log odds bahwa variabel respons bernilai 1.

Jadi, ketika kita menyesuaikan model regresi logistik, kita dapat menggunakan persamaan berikut untuk menghitung probabilitas bahwa observasi tertentu bernilai 1:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Kami kemudian menggunakan ambang probabilitas tertentu untuk mengklasifikasikan observasi sebagai 1 atau 0.

Misalnya, kita dapat mengatakan bahwa observasi dengan probabilitas lebih besar atau sama dengan 0,5 akan diklasifikasikan sebagai “1” dan semua observasi lainnya akan diklasifikasikan sebagai “0”.

Bagaimana menginterpretasikan hasil regresi logistik

Misalkan kita menggunakan model regresi logistik untuk memprediksi apakah seorang pemain bola basket tertentu akan direkrut ke NBA berdasarkan rata-rata rebound per game dan rata-rata poin per game.

Berikut hasil model regresi logistik:

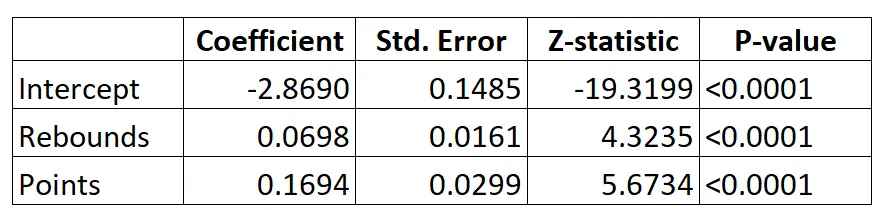
Dengan menggunakan koefisien, kita dapat menghitung probabilitas seorang pemain tertentu untuk masuk ke NBA berdasarkan rata-rata rebound dan poin per game menggunakan rumus berikut:

P(Draft) = e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(poin)} / (1+e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(poin) ) )}

Misalnya, seorang pemain rata-rata mencetak 8 rebound per game dan 15 poin per game. Menurut model, kemungkinan pemain ini masuk NBA adalah 0,557 .

P(Tertulis) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15 )} ) = 0,557

Karena probabilitas ini lebih besar dari 0,5, kami memperkirakan pemain ini akan direkrut.

Bandingkan dengan pemain yang hanya rata-rata mencetak 3 rebound dan 7 poin per game. Peluang pemain ini untuk masuk ke NBA adalah 0,186 .

P(Tertulis) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7 )} ) = 0,186

Karena probabilitas ini kurang dari 0,5, kami memperkirakan pemain ini tidak akan direkrut.

Asumsi Regresi Logistik

Regresi logistik menggunakan asumsi berikut:

1. Variabel responnya adalah biner. Diasumsikan bahwa variabel respon hanya dapat mengambil dua kemungkinan hasil.

2. Observasi bersifat independen. Diasumsikan bahwa observasi dalam kumpulan data tidak bergantung satu sama lain. Artinya, observasi tidak boleh berasal dari pengukuran berulang terhadap individu yang sama atau terkait satu sama lain dengan cara apa pun.

3. Tidak terdapat multikolinearitas yang serius antar variabel prediktor . Diasumsikan bahwa tidak ada satu pun variabel prediktor yang berkorelasi tinggi satu sama lain.

4. Tidak ada outlier yang ekstrim. Diasumsikan tidak ada outlier ekstrim atau observasi yang berpengaruh dalam kumpulan data.

5. Terdapat hubungan linier antara variabel prediktor dengan logit variabel respon . Hipotesis ini dapat diuji dengan menggunakan uji Box-Tidwell.

6. Ukuran sampelnya cukup besar. Biasanya, Anda harus memiliki minimal 10 kasus dengan hasil paling sedikit untuk setiap variabel penjelas. Misalnya, jika Anda memiliki 3 variabel penjelas dan probabilitas yang diharapkan dari hasil yang paling jarang terjadi adalah 0,20, maka Anda harus memiliki ukuran sampel minimal (10*3) / 0,20 = 150.

Lihat artikel ini untuk penjelasan mendetail tentang cara memverifikasi asumsi ini.