Cara melakukan regresi ols di r (dengan contoh)

Regresi kuadrat terkecil biasa (OLS) adalah metode yang memungkinkan kita menemukan garis yang paling menggambarkan hubungan antara satu atau lebih variabel prediktor dan variabel respons .

Metode ini memungkinkan kita menemukan persamaan berikut:

ŷ = b ₀ + b ₁ x

Emas:

• ŷ : Perkiraan nilai respons
• b ₀ : Asal garis regresi
• b ₁ : Kemiringan garis regresi

Persamaan ini dapat membantu kita memahami hubungan antara prediktor dan variabel respon, dan dapat digunakan untuk memprediksi nilai variabel respon dengan mempertimbangkan nilai variabel prediktor.

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi OLS di R.

Langkah 1: Buat datanya

Untuk contoh ini, kita akan membuat dataset yang berisi dua variabel berikut untuk 15 siswa:

• Jumlah total jam belajar
• Hasil ujian

Kami akan melakukan regresi OLS, menggunakan jam sebagai variabel prediktor dan nilai ujian sebagai variabel respon.

Kode berikut menunjukkan cara membuat dataset palsu ini di R:

 #create dataset
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Langkah 2: Visualisasikan datanya

Sebelum melakukan regresi OLS, mari buat diagram sebar untuk memvisualisasikan hubungan antara jam kerja dan nilai ujian:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size= 2 )

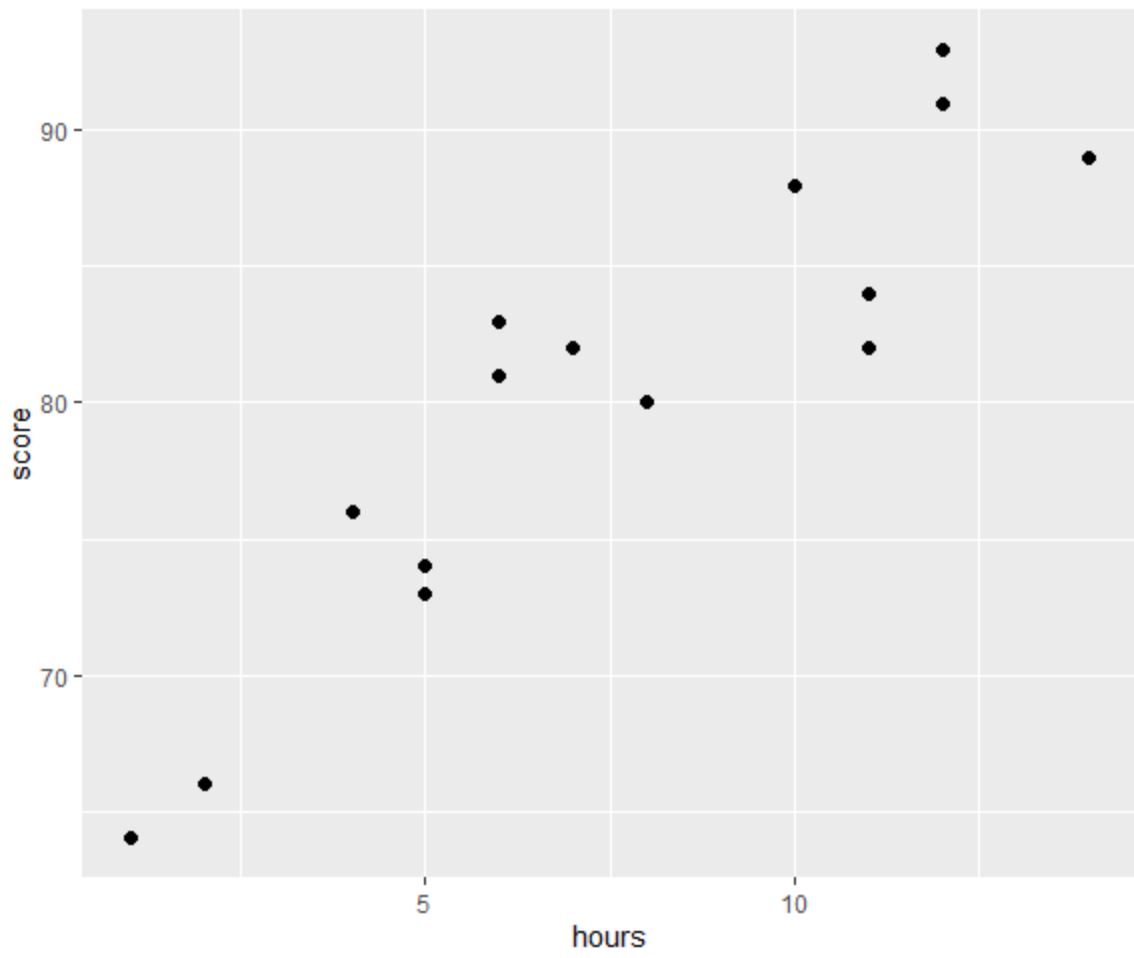
Salah satu dari empat asumsi regresi linier adalah adanya hubungan linier antara prediktor dan variabel respon.

Dari grafik terlihat bahwa hubungannya tampak linier. Seiring bertambahnya jumlah jam, skor juga cenderung meningkat secara linier.

Kemudian kita dapat membuat diagram kotak untuk memvisualisasikan distribusi hasil ujian dan memeriksa outlier.

Catatan : R didefinisikan suatu observasi sebagai outlier jika observasi tersebut 1,5 kali rentang antarkuartil di atas kuartil ketiga atau 1,5 kali rentang antarkuartil di bawah kuartil pertama.

Jika observasinya outlier, lingkaran kecil akan muncul di plot kotak:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(y=score)) +
  geom_boxplot() 

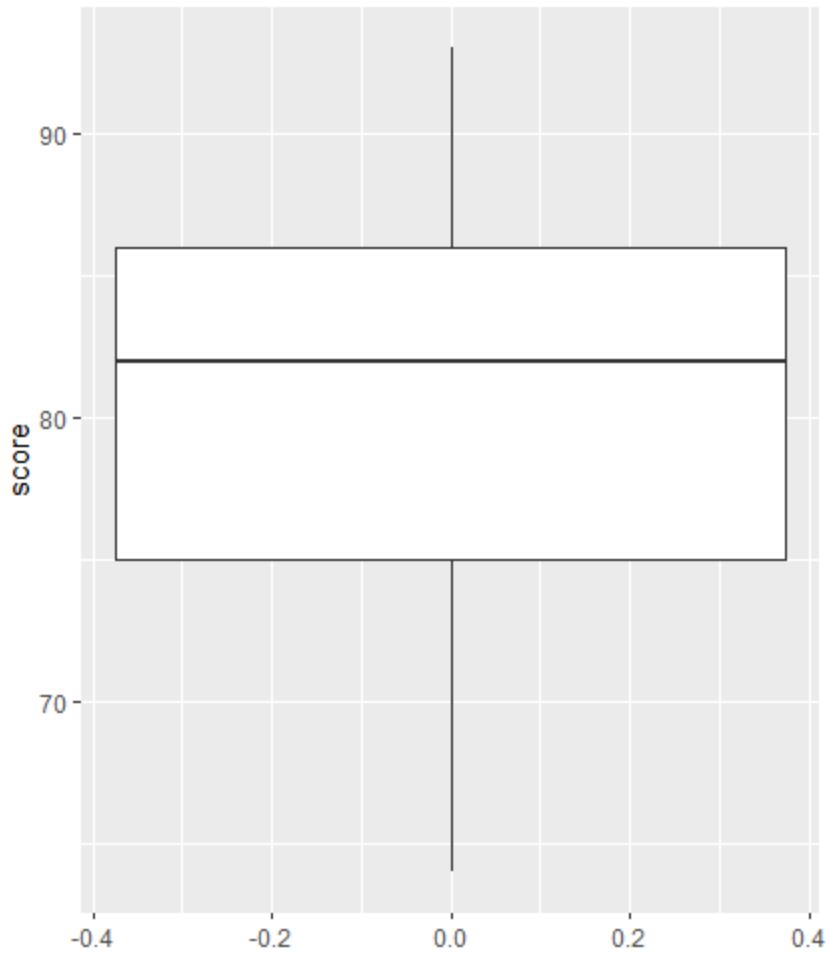
Tidak ada lingkaran kecil di boxplot, artinya tidak ada outlier di dataset kita.

Langkah 3: Lakukan Regresi OLS

Selanjutnya, kita dapat menggunakan fungsi lm() di R untuk melakukan regresi OLS, menggunakan jam sebagai variabel prediktor dan skor sebagai variabel respons:

 #fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Dari ringkasan model, kita dapat melihat bahwa persamaan regresi yang dipasang adalah:

Skor = 65.334 + 1.982*(jam)

Artinya, setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 1.982 poin.

Nilai awal sebesar 65.334 memberi tahu kita rata-rata nilai ujian yang diharapkan untuk seorang siswa yang belajar selama nol jam.

Kita juga dapat menggunakan persamaan ini untuk mencari nilai ujian yang diharapkan berdasarkan jumlah jam belajar seorang siswa.

Misalnya, seorang siswa yang belajar selama 10 jam harus mencapai nilai ujian 85,15 :

Skor = 65.334 + 1.982*(10) = 85.15

Berikut cara menafsirkan ringkasan model lainnya:

• Pr(>|t|): Ini adalah nilai p yang terkait dengan koefisien model. Karena nilai p untuk jam (2,25e-06) secara signifikan kurang dari 0,05, kita dapat mengatakan bahwa ada hubungan yang signifikan secara statistik antara jam dan skor .
• Multiple R-squared: Angka ini menunjukkan bahwa persentase variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar. Secara umum, semakin besar nilai R-squared suatu model regresi maka semakin baik pula variabel prediktor dalam memprediksi nilai variabel respon. Dalam hal ini, 83,1% variasi skor dapat dijelaskan oleh jam belajar.
• Kesalahan standar sisa: ini adalah jarak rata-rata antara nilai yang diamati dan garis regresi. Semakin rendah nilainya, semakin mampu garis regresi tersebut berkorespondensi dengan data yang diamati. Dalam hal ini, rata-rata skor yang diamati pada ujian menyimpang sebesar 3,641 poin dari skor yang diprediksi oleh garis regresi.
• F-statistik dan nilai p: F-statistik ( 63.91 ) dan nilai p yang sesuai ( 2.253e-06 ) memberi tahu kita signifikansi model regresi secara keseluruhan, yaitu apakah variabel prediktor dalam model berguna untuk menjelaskan variasi . dalam variabel respons. Karena nilai p dalam contoh ini kurang dari 0,05, model kami signifikan secara statistik dan jam dianggap berguna dalam menjelaskan variasi skor .

Langkah 4: Buat Plot Sisa

Terakhir, kita perlu membuat plot sisa untuk memeriksa asumsi homoskedastisitas dan normalitas .

Asumsi homoskedastisitas adalah residu model regresi mempunyai varians yang kurang lebih sama pada setiap level variabel prediktor.

Untuk memverifikasi bahwa asumsi ini terpenuhi, kita dapat membuat plot residu versus kecocokan .

Sumbu x menampilkan nilai yang dipasang dan sumbu y menampilkan residu. Selama residu tampak terdistribusi secara acak dan seragam di seluruh grafik di sekitar nilai nol, kita dapat berasumsi bahwa homoskedastisitas tidak dilanggar:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

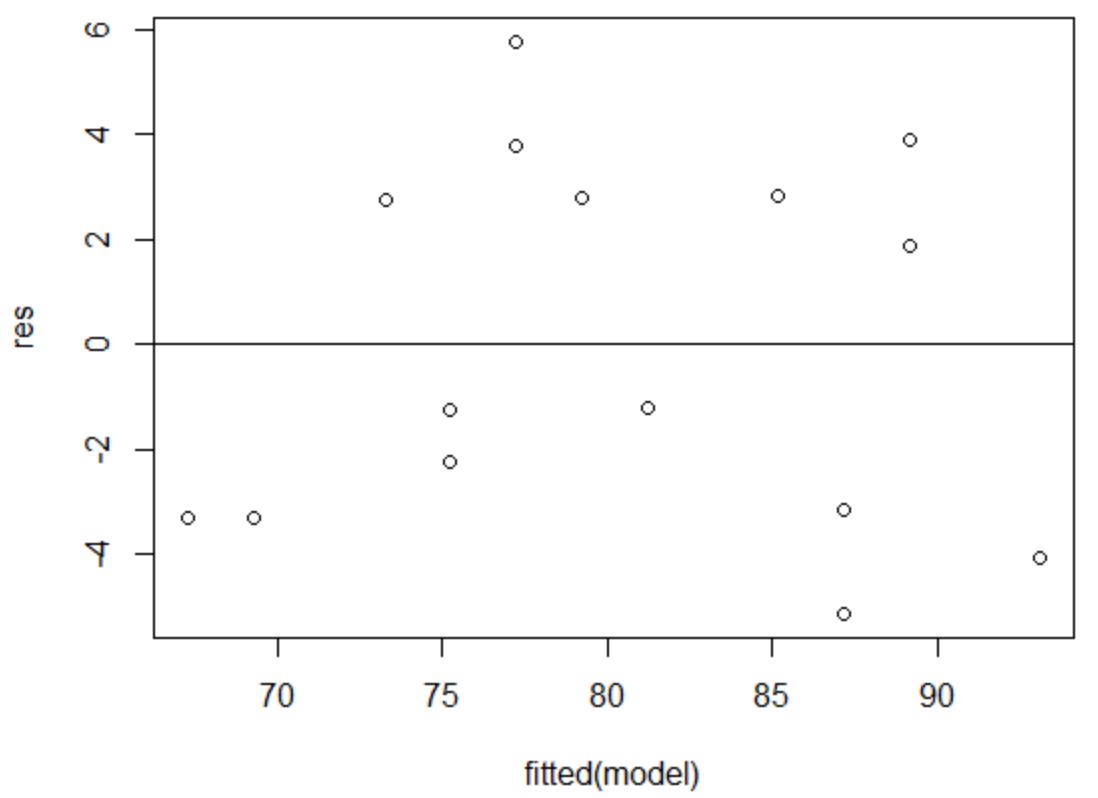
Residunya tampak tersebar secara acak di sekitar nol dan tidak menunjukkan pola yang nyata, sehingga asumsi ini terpenuhi.

Asumsi normalitas menyatakan bahwa residu model regresi mendekati terdistribusi normal.

Untuk memeriksa apakah asumsi ini terpenuhi, kita dapat membuat plot QQ . Jika titik-titik plot terletak pada garis kira-kira lurus membentuk sudut 45 derajat, maka data berdistribusi normal:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

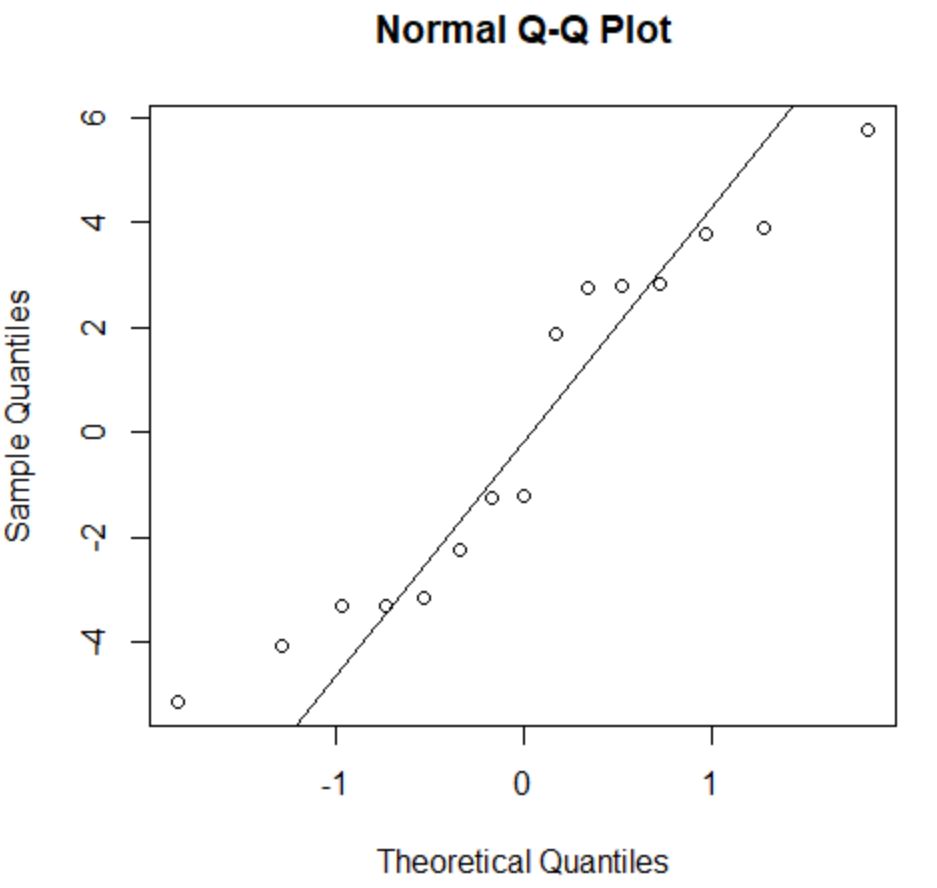
Residunya sedikit menyimpang dari garis 45 derajat, namun tidak cukup menimbulkan kekhawatiran serius. Kita dapat berasumsi bahwa asumsi normalitas terpenuhi.

Karena residu terdistribusi normal dan homoskedastis, kami memverifikasi bahwa asumsi model regresi OLS terpenuhi.

Dengan demikian, keluaran model kami dapat diandalkan.

Catatan : Jika satu atau lebih asumsi tidak terpenuhi, kami dapat mencoba mengubah data kami.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi eksponensial di R
Bagaimana melakukan regresi kuadrat terkecil tertimbang di R