Regresi polinomial

Oleh Benjamin anderson Agustus 2, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu regresi polinomial dalam statistik dan bagaimana cara kerjanya. Selain itu, Anda akan dapat melihat contoh pelaksanaan regresi polinomial.

Apa itu regresi polinomial?

Regresi polinomial , atau regresi polinomial , adalah model regresi yang hubungan antara variabel bebas X dan variabel terikat Y dimodelkan menggunakan polinomial.

Misalnya, persamaan model regresi polinomial kuadrat adalah y=β ₀ +β ₁ x+β ₂ x ² +ε.

Regresi polinomial berguna untuk menyesuaikan kumpulan data yang grafiknya berupa kurva polinomial. Jadi, jika dot plot suatu sampel data berbentuk parabola, sebaiknya dibuat model regresi kuadratik daripada model regresi linier. Dengan cara ini, persamaan model regresi akan lebih sesuai dengan sampel data.

Perhatikan bahwa regresi polinomial adalah jenis regresi nonlinier, sama seperti regresi eksponensial dan regresi logaritmik.

Rumus Regresi Polinomial

Persamaan model regresi polinomial adalah y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Emas:

$y$

adalah variabel terikat.
$x$

adalah variabel independen.
$\beta_0$

adalah konstanta persamaan regresi polinomial.
$\beta_i$

adalah koefisien regresi yang terkait dengan variabel

$x^i$

.
$\bm{\varepsilon}$

Ini adalah kesalahan atau sisa, yaitu selisih antara nilai yang diamati dan nilai yang diestimasi oleh model.

Jadi jika kita mempunyai sampel dengan jumlah total

$n$

pengamatan, kita dapat mengusulkan model regresi polinomial dalam bentuk matriks:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

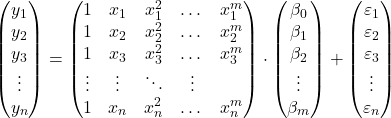
Ekspresi matriks di atas dapat ditulis ulang dengan memberikan huruf pada setiap matriks:

$Y=X\beta+\varepsilon$

Jadi, dengan menerapkan kriteria kuadrat terkecil , kita dapat memperoleh rumus untuk memperkirakan koefisien model regresi polinomial :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Namun, melakukan penghitungan ini dengan tangan sangat melelahkan dan memakan waktu, sehingga akan lebih mudah menggunakan perangkat lunak komputer (seperti Minitab atau Excel) yang memungkinkan Anda menjalankan model regresi polinomial dengan lebih cepat.

Contoh model regresi polinomial

Sekarang setelah kita mengetahui definisi regresi polinomial dan cara kerjanya, mari kita lihat contoh nyata untuk memahami konsep tersebut sepenuhnya.

Pertama-tama, perlu diingat bahwa model regresi polinomial harus dilakukan jika grafik data berbentuk kurva polinomial. Misalnya, jika dotplot berbentuk kurva kubik, maka kita perlu membuat model regresi polinomial derajat ketiga.

Jadi, seperti yang Anda lihat pada gambar berikut, dot plot data kita berbentuk kuadrat, karena semakin kita meningkatkan nilai variabel independen, maka variabel dependen akan tumbuh lebih cepat. Dalam hal ini model regresi linier telah dilakukan dan seperti yang Anda lihat, model tersebut tidak sesuai dengan titik-titiknya karena memiliki bagian yang garisnya berada di bawah semua titik dan bagian yang garisnya berada di atasnya.

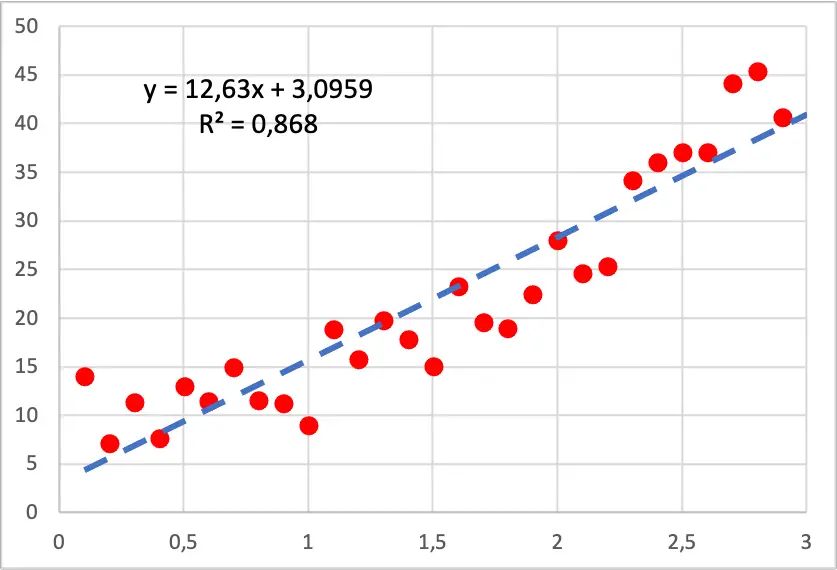
Di sisi lain, jika kita menjalankan model regresi polinomial kuadrat, model tersebut akan lebih cocok dengan data sampel, seperti yang Anda lihat pada gambar di bawah.

Selain itu, ketika mengembangkan model regresi polinomial, koefisien determinasi meningkat pesat dari 86,80% menjadi 94,05%. Oleh karena itu, model regresi baru menjelaskan kumpulan data dengan lebih baik.

Di sisi lain, indikasi lain bahwa kita perlu melakukan regresi polinomial adalah memplot residu. Jika dalam regresi linier grafik residunya berbentuk parabola atau polinomial jenis lain, maka model regresi polinomial tentu lebih cocok dengan data yang diteliti.

Jenis regresi nonlinier lainnya

Pada dasarnya ada tiga jenis regresi nonlinier:

Regresi Polinomial – Persamaan model regresi berbentuk polinomial.
Regresi logaritma : diambil logaritma variabel bebasnya.
Regresi Eksponensial : Variabel independen terletak pada eksponen persamaan.

➤ Lihat: Regresi logaritmik
➤ Lihat: Regresi Eksponensial

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya