Cara melakukan regresi polinomial di sas

Jenis analisis regresi yang paling umum adalah regresi linier sederhana , digunakan ketika variabel prediktor dan variabel respons mempunyai hubungan linier.

Namun terkadang hubungan antara variabel prediktor dan variabel respon bersifat nonlinier.

Dalam kasus ini, masuk akal untuk menggunakan regresi polinomial , yang dapat menjelaskan hubungan nonlinier antar variabel.

Contoh berikut menunjukkan cara melakukan regresi polinomial di SAS.

Contoh: Regresi Polinomial di SAS

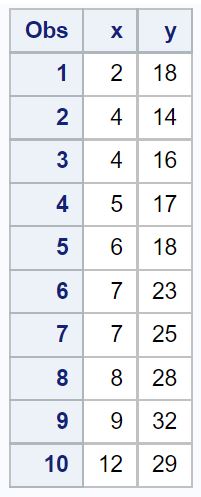
Anggaplah kita memiliki kumpulan data berikut di SAS:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
2 18
4 14
4 16
5 17
6 18
7 23
7 25
8 28
9 32
12 29
;
run ;

/*view dataset*/
proc print data =my_data;

Sekarang misalkan kita membuat scatterplot untuk memvisualisasikan hubungan antara variabel x dan y dalam dataset:

 /*create scatter plot of x vs. y*/
proc sgplot data =my_data;
    scatter x =x y =y;
run ; 

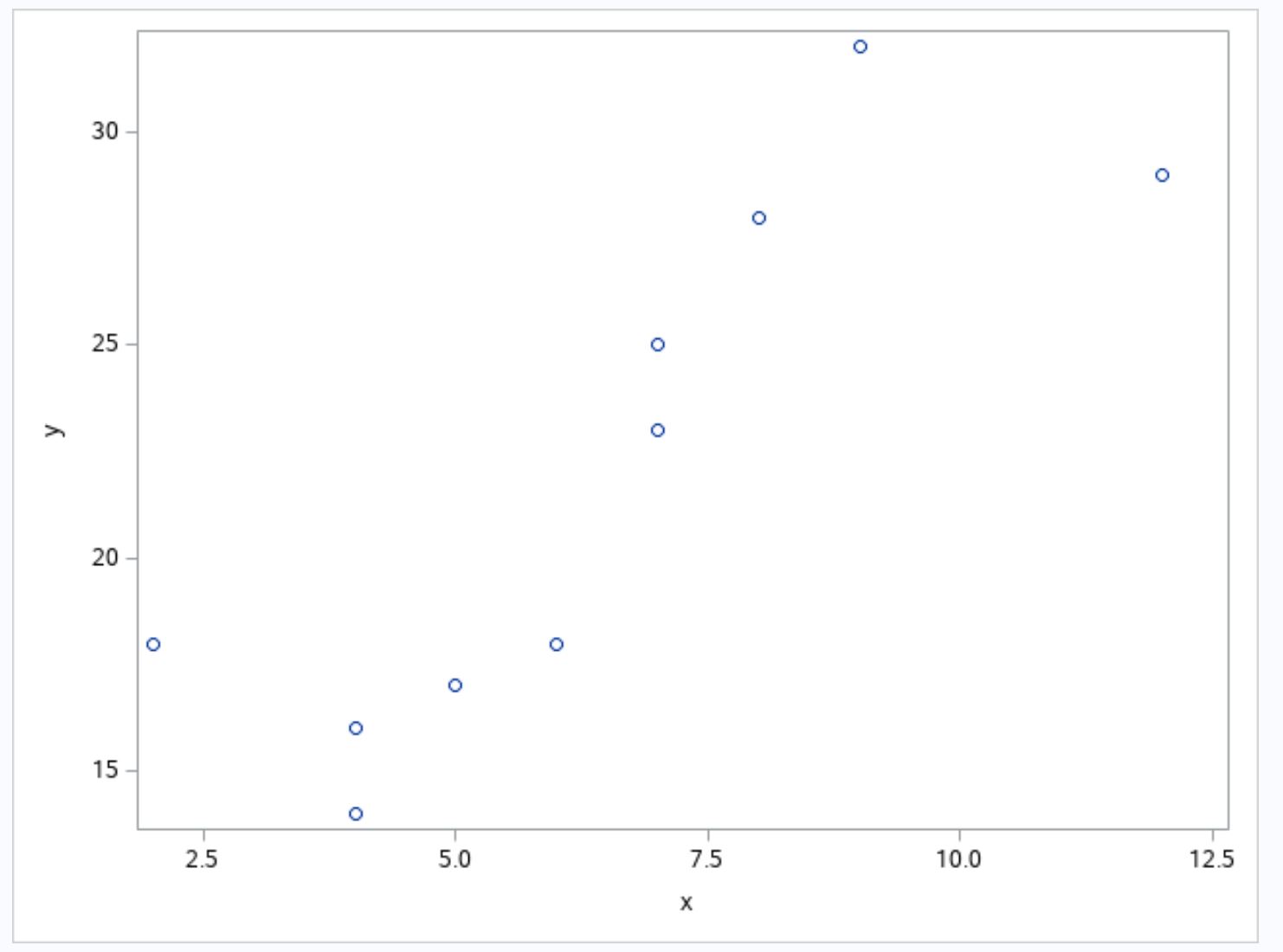
Dari grafik terlihat bahwa hubungan antara x dan y berbentuk kubik.

Jadi, kita dapat menentukan dua variabel prediktor baru dalam kumpulan data kita (x ² dan x ³ ), lalu menggunakan proc reg agar sesuai dengan model regresi polinomial menggunakan variabel prediktor berikut:

 /*create dataset with new predictor variables*/
data my_data;
    input xy;
    x2 = x** 2 ;
    x3 = x** 3 ;
    datalines ;
2 18
4 14
4 16
5 17
6 18
7 23
7 25
8 28
9 32
12 29
;
run ;

/*fit polynomial regression model*/
proc reg data =my_data;
    model y = x x2 x3;
run ;

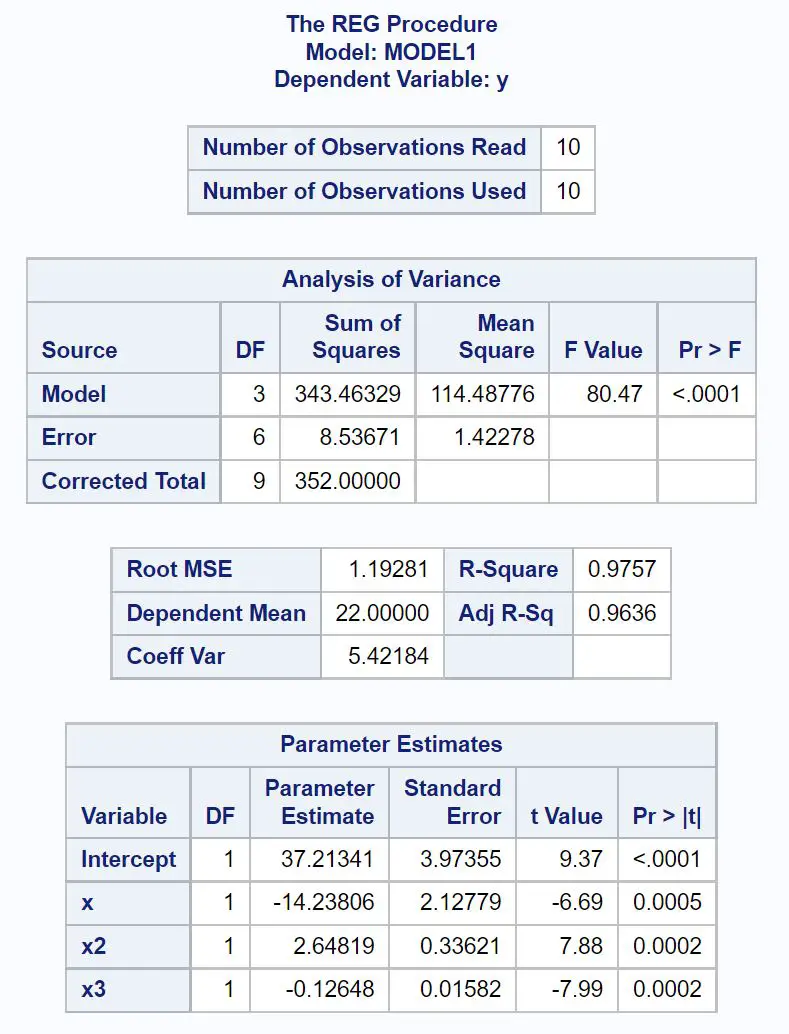
Dari tabel Estimasi Parameter , kita dapat menemukan estimasi koefisien dan menulis persamaan regresi polinomial yang sesuai sebagai:

kamu = 37,213 – 14,238x + 2,648x ² – 0,126x ³

Persamaan ini dapat digunakan untuk mencari nilai yang diharapkan dari variabel respon dengan adanya nilai tertentu dari variabel prediktor.

Misalnya, jika xa bernilai 4, maka y seharusnya bernilai 14,565:

kamu = 37,213 – 14,238(4) + 2,648(4) ² – 0,126(4) ³ = 14,565

Kita juga dapat melihat bahwa model regresi polinomial memiliki nilai R-kuadrat yang disesuaikan sebesar 0,9636 , yang sangat mendekati satu dan menunjukkan bahwa model tersebut berfungsi dengan baik dalam menyesuaikan kumpulan data.

Terkait: Cara Menafsirkan R-Squared yang Disesuaikan (Dengan Contoh)

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara melakukan regresi linier sederhana di SAS
Cara melakukan regresi linier berganda di SAS
Cara melakukan regresi kuantil di SAS