Regresi polinomial di r (langkah demi langkah)

Regresi polinomial adalah teknik yang dapat kita gunakan ketika hubungan antara variabel prediktor dan variabel respon bersifat nonlinier.

Jenis regresi ini berbentuk:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

di mana h adalah “derajat” polinomial.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan regresi polinomial di R.

Langkah 1: Buat datanya

Untuk contoh ini, kita akan membuat dataset yang berisi jumlah jam belajar dan nilai ujian akhir untuk kelas yang terdiri dari 50 siswa:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Langkah 2: Visualisasikan datanya

Sebelum memasang model regresi ke data, pertama-tama mari buat diagram sebar untuk memvisualisasikan hubungan antara jam belajar dan nilai ujian:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

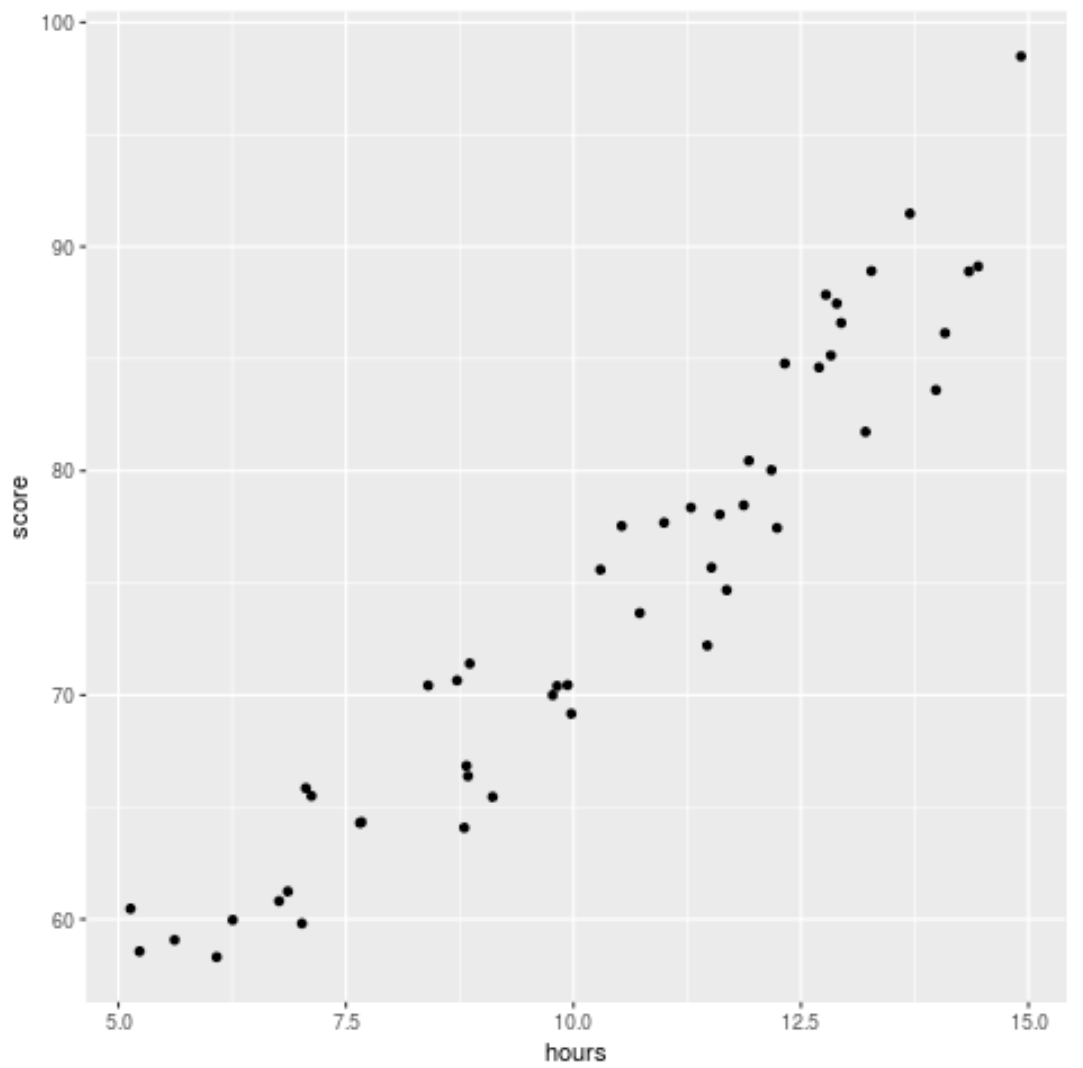
Kita dapat melihat bahwa data memiliki hubungan yang sedikit kuadrat, yang menunjukkan bahwa regresi polinomial mungkin lebih cocok dengan data dibandingkan regresi linier sederhana.

Langkah 3: Sesuaikan model regresi polinomial

Selanjutnya, kita akan memasang lima model regresi polinomial berbeda dengan derajat h = 1…5 dan menggunakan validasi silang k-fold dengan k = 10 kali untuk menghitung uji MSE untuk setiap model:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

Dari hasilnya kita dapat melihat pengujian MSE untuk masing-masing model:

• Uji MSE dengan derajat h = 1 : 9,80
• Uji MSE dengan derajat h = 2 : 8,75
• Uji MSE dengan derajat h = 3 : 9,60
• Uji MSE dengan derajat h = 4 : 10,59
• Tes MSE dengan derajat h = 5 : 13,55

Model dengan uji MSE terendah ternyata adalah model regresi polinomial dengan derajat h = 2.

Ini cocok dengan intuisi kita dari diagram sebar asli: model regresi kuadratik paling sesuai dengan data.

Langkah 4: Analisis model akhir

Terakhir, kita dapat memperoleh koefisien model dengan kinerja terbaik:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dari hasilnya, kita dapat melihat bahwa model akhir yang dipasang adalah:

Skor = 54,00526 – 0,07904*(jam) + 0,18596*(jam) ²

Kita dapat menggunakan persamaan ini untuk memperkirakan skor yang akan diterima siswa berdasarkan jumlah jam belajar.

Misalnya, seorang siswa yang belajar 10 jam seharusnya mendapat nilai 71,81 :

Skor = 54,00526 – 0,07904*(10) + 0,18596*(10) ² = 71,81

Kita juga dapat memplot model yang dipasang untuk melihat seberapa cocok model tersebut dengan data mentah:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

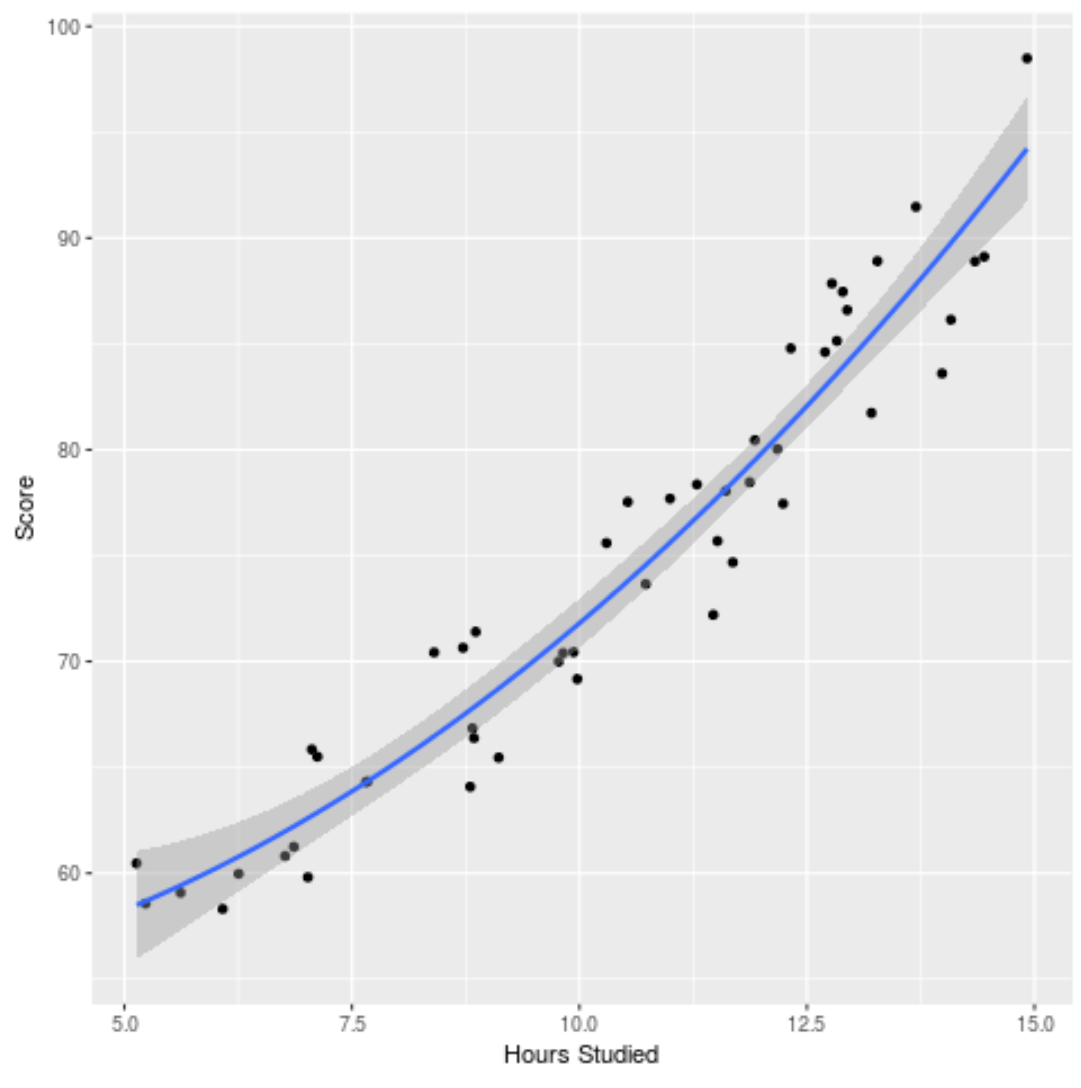
Anda dapat menemukan kode R lengkap yang digunakan dalam contoh ini di sini .