Apa yang dimaksud dengan residu dalam statistik?

Residual adalah selisih antara nilai observasi dan nilai prediksi dalam analisis regresi .

Ini dihitung sebagai berikut:

Sisa = Nilai yang diamati – Nilai yang diprediksi

Ingatlah bahwa tujuan regresi linier adalah untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respon . Untuk melakukan hal ini, regresi linier menemukan garis yang paling “sesuai” dengan data, yang disebut garis regresi kuadrat terkecil .

Garis ini menghasilkan prediksi untuk setiap observasi dalam kumpulan data, namun prediksi yang dibuat oleh garis regresi kecil kemungkinannya akan sama persis dengan nilai observasi.

Selisih antara nilai prediksi dan nilai observasi merupakan sisa. Jika kita memplot nilai observasi dan menempatkan garis regresi yang dipasang, residu untuk setiap observasi akan menjadi jarak vertikal antara observasi dan garis regresi:

Suatu observasi mempunyai residu positif jika nilainya lebih besar dari nilai prediksi yang dibuat oleh garis regresi.

Sebaliknya suatu observasi mempunyai residu negatif jika nilainya lebih kecil dari nilai prediksi yang dibuat oleh garis regresi.

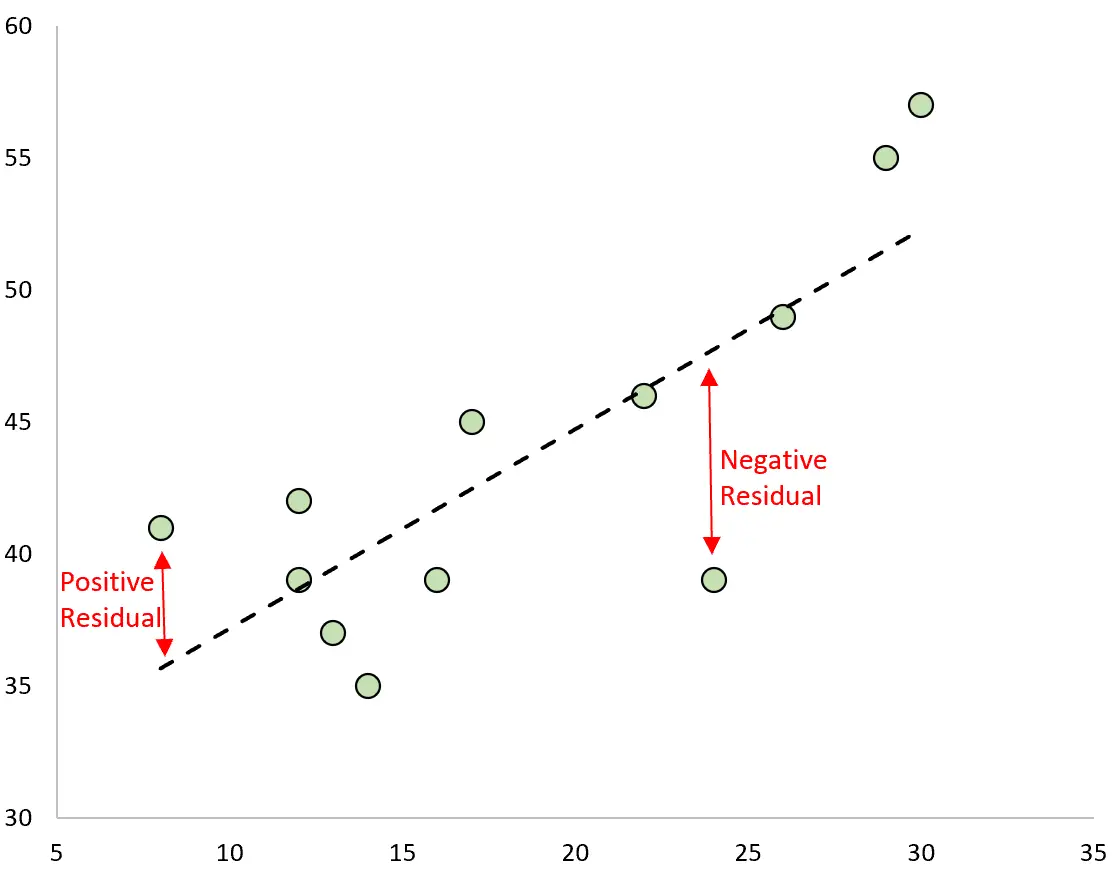
Beberapa observasi akan mempunyai residu positif sementara pengamatan lainnya akan memiliki residu negatif, namun semua residu akan berjumlah nol .

Contoh penghitungan residu

Misalkan kita memiliki kumpulan data berikut dengan total 12 observasi:

Jika kita menggunakan perangkat lunak statistik (seperti R , Excel , Python , Stata , dll.) untuk menyesuaikan garis regresi linier dengan kumpulan data ini, kita akan menemukan bahwa garis yang paling sesuai adalah:

kamu = 29,63 + 0,7553x

Dengan menggunakan baris ini, kita dapat menghitung nilai prediksi untuk setiap nilai Y berdasarkan nilai X. Misalnya, nilai prediksi observasi pertama adalah:

kamu = 29,63 + 0,7553*(8) = 35,67

Kami kemudian dapat menghitung sisa pengamatan ini sebagai berikut:

Sisa = Nilai teramati – Nilai prediksi = 41 – 35,67 = 5,33

Kita dapat mengulangi proses ini untuk mencari sisa setiap observasi:

Jika kita membuat plot sebar untuk memvisualisasikan pengamatan dengan garis regresi yang dipasang, kita akan melihat bahwa beberapa pengamatan terletak di atas garis sementara yang lain berada di bawah garis:

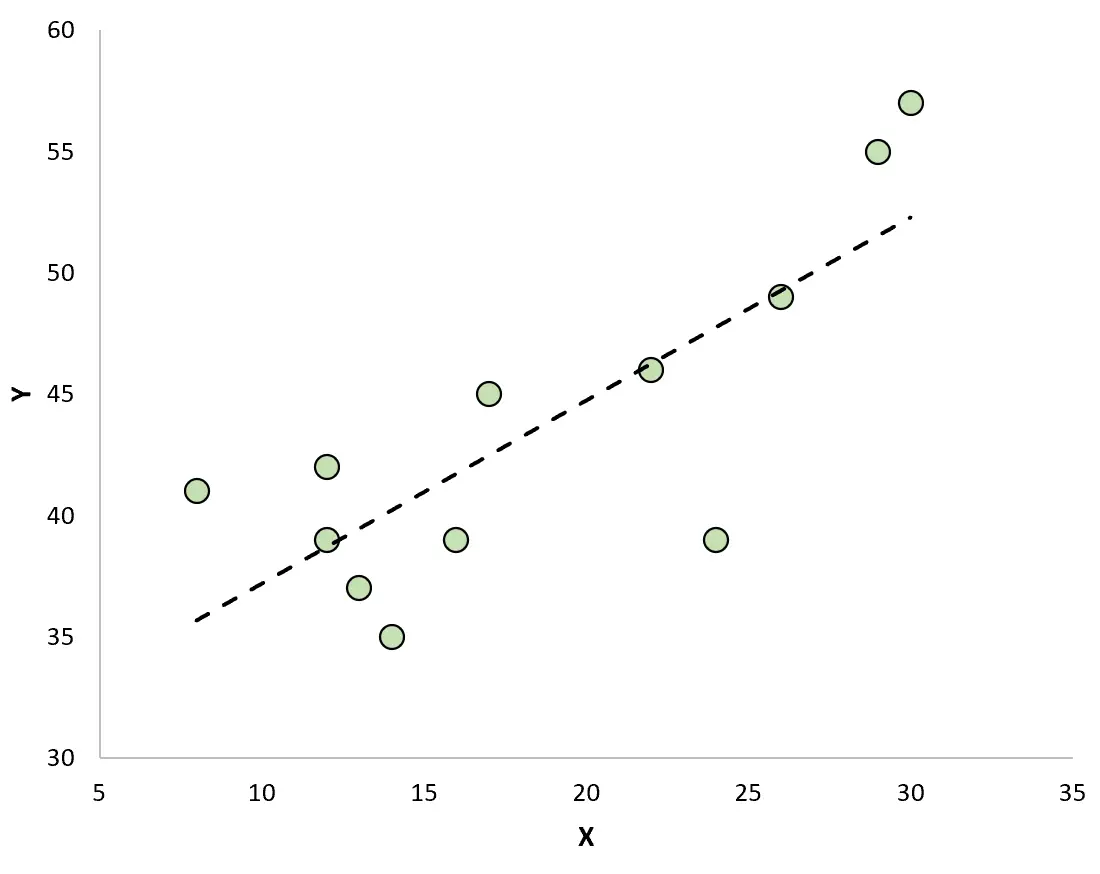
Sifat residu

Residu memiliki sifat-sifat berikut:

• Setiap observasi dalam kumpulan data memiliki residu yang sesuai. Jadi, jika suatu dataset berisi total 100 observasi, model akan menghasilkan 100 nilai prediksi, sehingga menghasilkan total 100 residu.
• Jumlah semua residu adalah nol.
• Nilai rata-rata residunya adalah nol.

Bagaimana residu digunakan dalam praktiknya?

Dalam praktiknya, residu digunakan untuk tiga alasan berbeda dalam regresi:

1. Evaluasi kecukupan model.

Setelah kita menghasilkan garis regresi yang sesuai, kita dapat menghitung jumlah sisa kuadrat (RSS) , yang merupakan jumlah dari semua sisa kuadrat. Semakin rendah RSS, semakin baik model regresi tersebut sesuai dengan data.

2. Periksa asumsi normalitas.

Salah satu asumsi utama regresi linier adalah bahwa residunya terdistribusi normal.

Untuk menguji hipotesis tersebut, kita dapat membuat plot QQ, yaitu jenis plot yang dapat kita gunakan untuk menentukan apakah residu suatu model mengikuti distribusi normal atau tidak.

Jika titik-titik pada plot kira-kira membentuk garis lurus diagonal, maka asumsi normalitas terpenuhi.

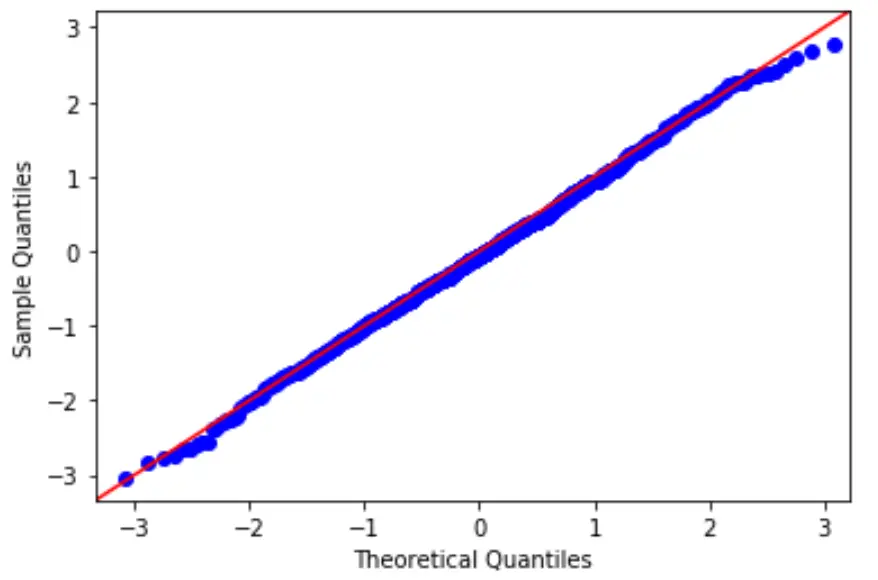
3. Periksa asumsi homoskedastisitas.

Asumsi penting lainnya dari regresi linier adalah bahwa residu memiliki varian yang konstan pada setiap tingkat x. Hal ini disebut homoskedastisitas. Jika hal ini tidak terjadi, maka residunya mengalami heteroskedastisitas .

Untuk memeriksa apakah asumsi ini terpenuhi, kita dapat membuat plot residu , yaitu plot sebar yang menunjukkan residu terhadap nilai prediksi model.

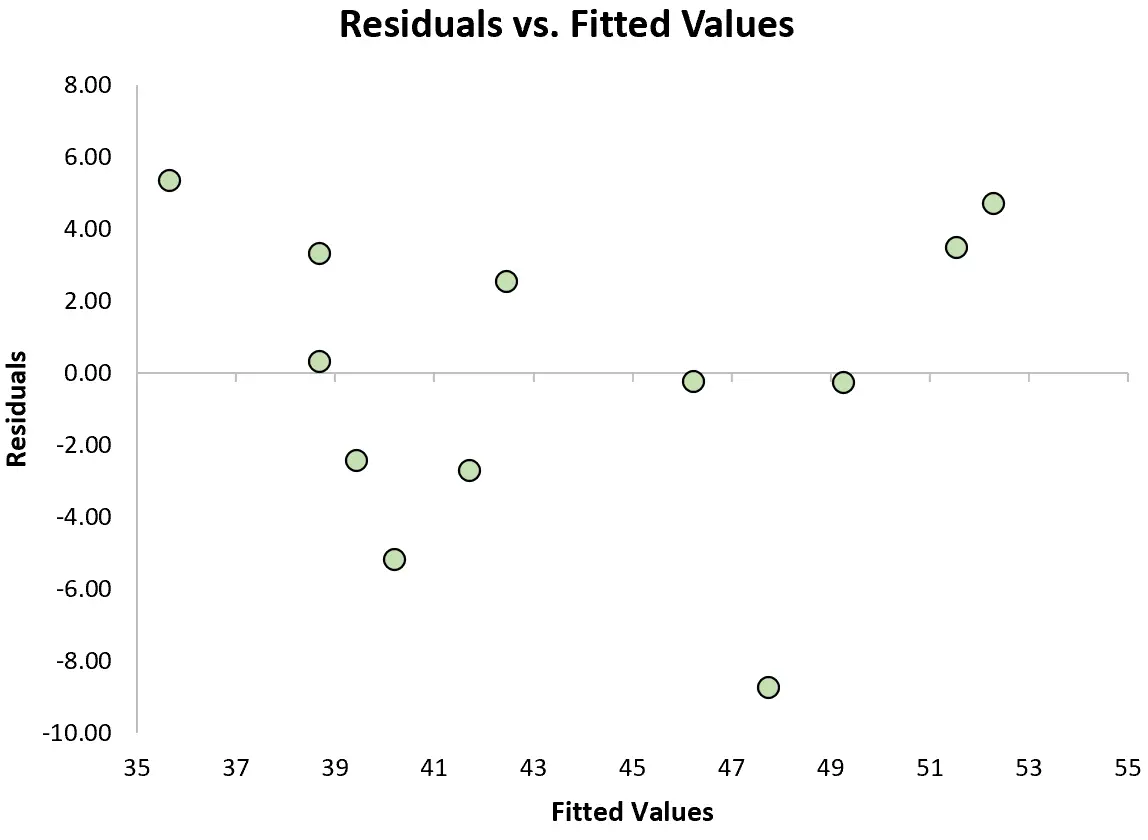
Jika residunya kira-kira terdistribusi merata di sekitar nol pada grafik tanpa tren yang jelas, maka secara umum asumsi homoskedastisitas terpenuhi.

Sumber daya tambahan

Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Empat asumsi regresi linier
Cara Membuat Plot Sisa di Excel