Bagaimana menganalisis residu dalam model anova
ANOVA (“analisis varians”) adalah jenis model yang digunakan untuk menentukan apakah terdapat perbedaan yang signifikan antara rata-rata tiga atau lebih kelompok independen.
kami memasangkan ANOVA Setiap kali model diterapkan pada kumpulan data, akan selalu ada residu – residu ini mewakili perbedaan antara masing-masing observasi individu dan rata-rata kelompok asal observasi tersebut.
Contoh berikut menunjukkan cara menghitung residu untuk model ANOVA dalam praktiknya.
Contoh: Perhitungan residu di ANOVA
Misalkan kita merekrut 90 orang untuk berpartisipasi dalam eksperimen penurunan berat badan yang mana kita secara acak menugaskan 30 orang untuk mengikuti Program A, Program B, atau Program C selama sebulan.
Kita dapat melakukan ANOVA satu arah untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara penurunan berat badan yang dihasilkan dari ketiga program.
Misalkan kita menghitung rata-rata penurunan berat badan individu yang berpartisipasi dalam setiap program sebagai berikut:
- Program A : 1,58 pon
- Program B : 2,56 pon
- Program C : 4,13 pon
Sisa dari model ANOVA adalah selisih antara penurunan berat badan masing-masing individu dan rata-rata penurunan berat badan program mereka.
Misalnya, tabel berikut menunjukkan cara menghitung residu untuk 10 individu berbeda dalam penelitian:
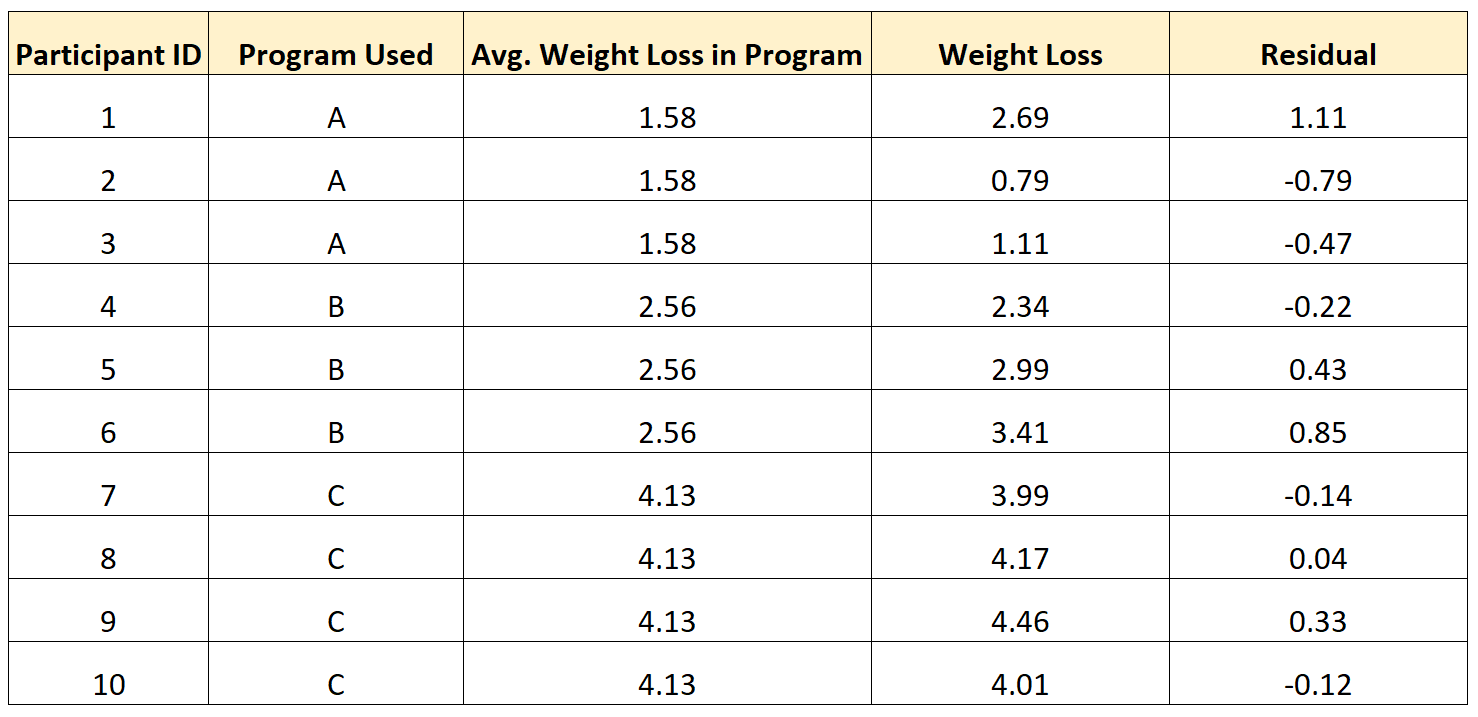
Perhatikan pola berikut:
- Individu yang memiliki nilai di atas rata-rata kelompoknya memiliki sisa positif .
- Individu yang memiliki nilai lebih rendah dari rata-rata kelompoknya mempunyai sisa negatif .
Dalam praktiknya, kami akan menghitung residu untuk 90 individu.
Cara menggunakan residu untuk memeriksa normalitas
Salah satu asumsi ANOVA adalah residunya terdistribusi normal.
Cara paling umum untuk memverifikasi asumsi ini adalah dengan membuat plot QQ .
Jika residunya berdistribusi normal, maka titik-titik pada plot QQ akan terletak pada garis lurus diagonal.
Berikut tampilan plot QQ pada contoh sebelumnya:
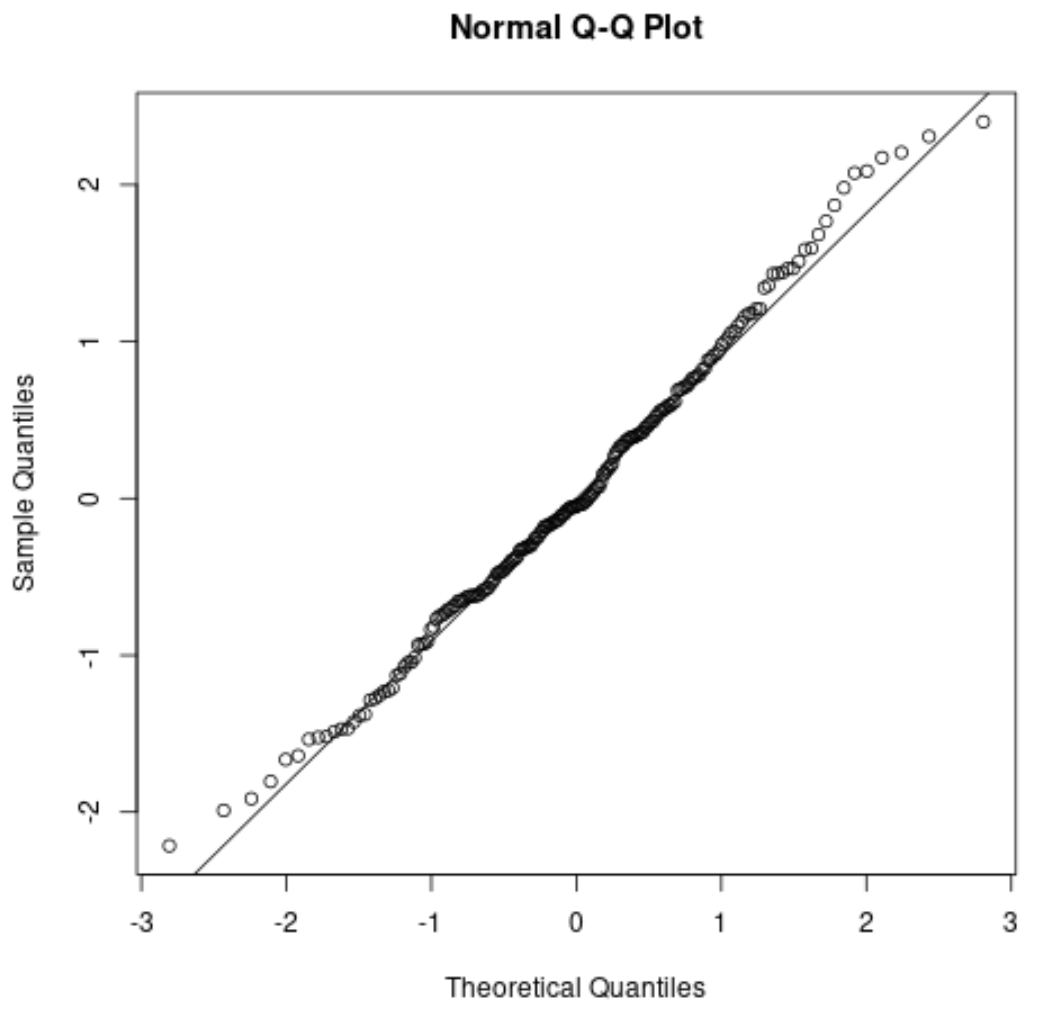
Ujungnya sedikit melenceng dari garis lurus diagonal pada ujung ekornya, namun secara umum ujungnya jatuh cukup baik mengikuti garis diagonal. Hal ini menunjukkan bahwa asumsi normalitas mungkin terpenuhi.
Sebagai referensi, berikut adalah tampilan plot QQ untuk residu yang tidak terdistribusi normal:
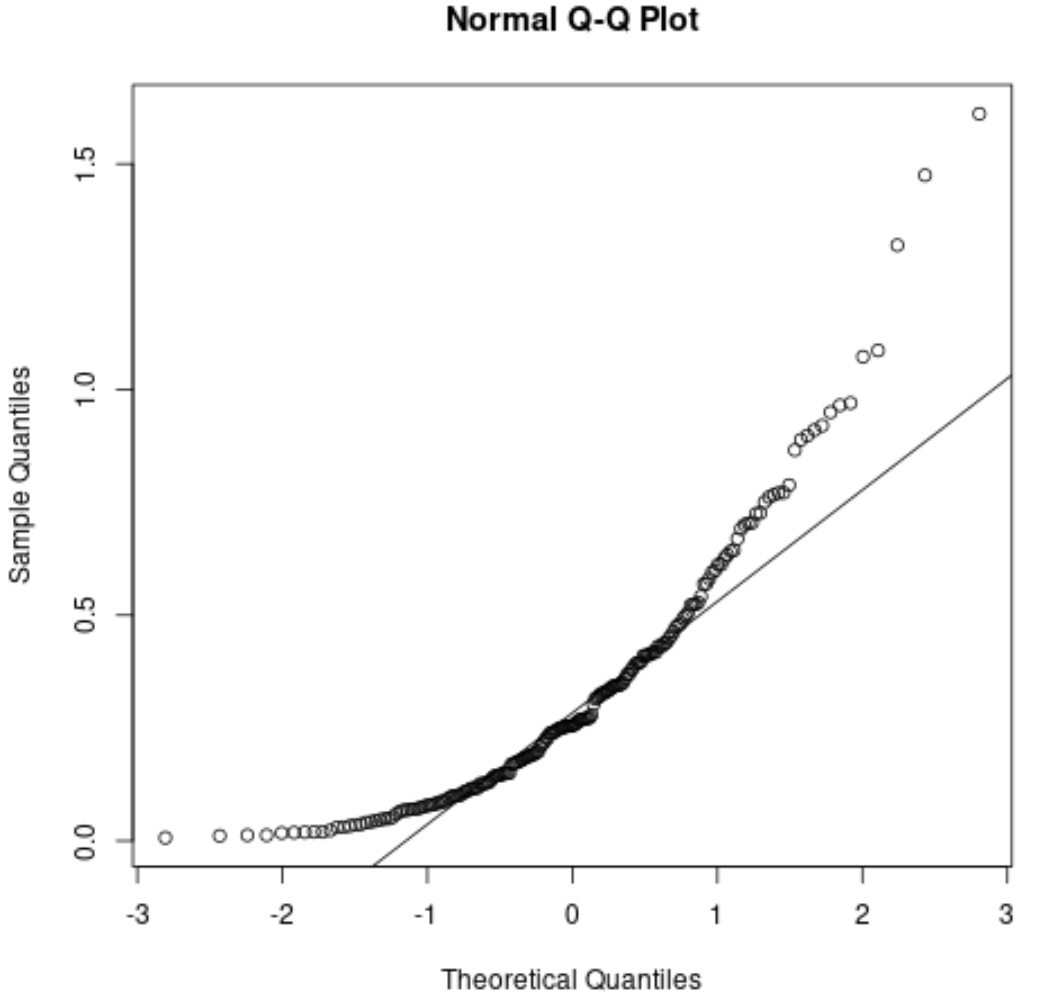
Titik-titik tersebut sangat menyimpang dari garis lurus diagonal yang menunjukkan bahwa residu tidak berdistribusi normal.
Lihat tutorial berikut untuk mempelajari cara membuat plot QQ di berbagai perangkat lunak:
Sumber daya tambahan
Artikel berikut memberikan informasi tambahan tentang model ANOVA:
Pengantar ANOVA Satu Arah
Bagaimana cara memeriksa asumsi ANOVA
4 contoh penggunaan ANOVA dalam kehidupan nyata
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya