Apa itu residu pearson? (definisi & #038; contoh)
Residu Pearson digunakan dalam uji independensi chi-kuadrat untuk menganalisis perbedaan antara jumlah sel yang diamati dan jumlah sel yang diharapkan dalam tabel kontingensi.
Rumus untuk menghitung sisa Pearson adalah:
r ij = (O ij – E ij ) / √ E ij
Emas:
- r ij : Residu Pearson untuk sel kolom ke i dan baris ke j
- O ij : Nilai yang diamati untuk sel kolom ke i dan baris ke j
- E ij : Nilai yang diharapkan untuk sel pada kolom ke -i dan baris ke -j
Ukuran serupa adalah residu Pearson yang distandarisasi (disesuaikan) , yang dihitung sebagai berikut:
r ij = (O ij – E ij ) / √ E ij (1-n i+ )(1-n +j )
Emas:
- r ij : Residu Pearson untuk sel kolom ke i dan baris ke j
- O ij : Nilai yang diamati untuk sel kolom ke i dan baris ke j
- E ij : Nilai yang diharapkan untuk sel pada kolom ke -i dan baris ke -j
- p i+ : Jumlah baris dibagi total keseluruhan
- p + j : Total kolom dibagi total keseluruhan
Residual Pearson yang terstandarisasi berdistribusi normal dengan rata-rata 0 dan deviasi standar 1. Residual Pearson yang terstandarisasi dengan nilai absolut di atas ambang batas tertentu (misalnya 2 atau 3) menunjukkan adanya ketidaksesuaian.
Contoh berikut menunjukkan cara menghitung residu Pearson dalam praktiknya.
Contoh: Perhitungan residu Pearson
Misalkan peneliti ingin menggunakan uji independensi chi-square untuk menentukan apakah gender dikaitkan dengan preferensi terhadap suatu partai politik atau tidak.
Mereka memutuskan untuk mengambil sampel acak sederhana dari 500 pemilih dan menanyakan preferensi partai politik mereka.
Tabel kontingensi berikut menyajikan hasil survei:
| Republik | Demokrat | Mandiri | Total | |
| Pria | 120 | 90 | 40 | 250 |
| Perempuan | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Sebelum menghitung residu Pearson, terlebih dahulu kita harus menghitung jumlah yang diharapkan untuk setiap sel dalam tabel kontingensi. Untuk melakukannya, kita dapat menggunakan rumus berikut:
Nilai yang diharapkan = (jumlah baris * jumlah kolom) / jumlah tabel.
Misalnya, nilai yang diharapkan untuk pria Partai Republik adalah: (230*250) / 500 = 115 .
Kita bisa mengulangi rumus ini untuk mendapatkan nilai yang diharapkan untuk setiap sel tabel:
| Republik | Demokrat | Mandiri | Total | |
| Pria | 115 | 92.5 | 42.5 | 250 |
| Perempuan | 115 | 92.5 | 42.5 | 250 |
| Total | 230 | 185 | 85 | 500 |
Kemudian kita dapat menghitung sisa Pearson untuk setiap sel dalam tabel.
Misalnya, sisa Pearson untuk sel yang berisi laki-laki Partai Republik akan dihitung sebagai berikut:
- r ij = (O ij – E ij ) / √ E ij
- r ij = (120 – 115) / √ 115
- r ij = 0,466
Kita dapat mengulangi rumus ini untuk mendapatkan sisa Pearson untuk setiap sel dalam tabel:
| Republik | Demokrat | Mandiri | |
| Pria | 0,446 | -0,259 | -0,383 |
| Perempuan | -0,446 | 0,259 | 0,383 |
Kemudian kita dapat menghitung sisa Pearson standar untuk setiap sel dalam tabel.
Misalnya, sisa Pearson yang distandarisasi untuk sel yang berisi laki-laki Partai Republik akan dihitung sebagai berikut:
- r ij = (O ij – E ij ) / √ E ij (1-p i+ )(1-p +j )
- r ij = (120 – 115) / √ 115(1-250/500)(1-230/500)
- r ij = 0,897
Kita dapat mengulangi rumus ini untuk mendapatkan sisa Pearson standar untuk setiap sel dalam tabel:
| Republik | Demokrat | Mandiri | |
| Pria | 0,897 | -0,463 | -0,595 |
| Perempuan | -0,897 | 0,463 | 0,595 |
Kita dapat melihat bahwa tidak ada residu Pearson yang terstandarisasi yang memiliki nilai absolut lebih besar dari 3, yang menunjukkan bahwa tidak ada sel yang berkontribusi terhadap kurangnya kecocokan yang signifikan.
Jika kita menggunakan kalkulator online ini untuk melakukan uji independensi chi-kuadrat, kita akan menemukan bahwa nilai p dari tes tersebut adalah 0,649198 .
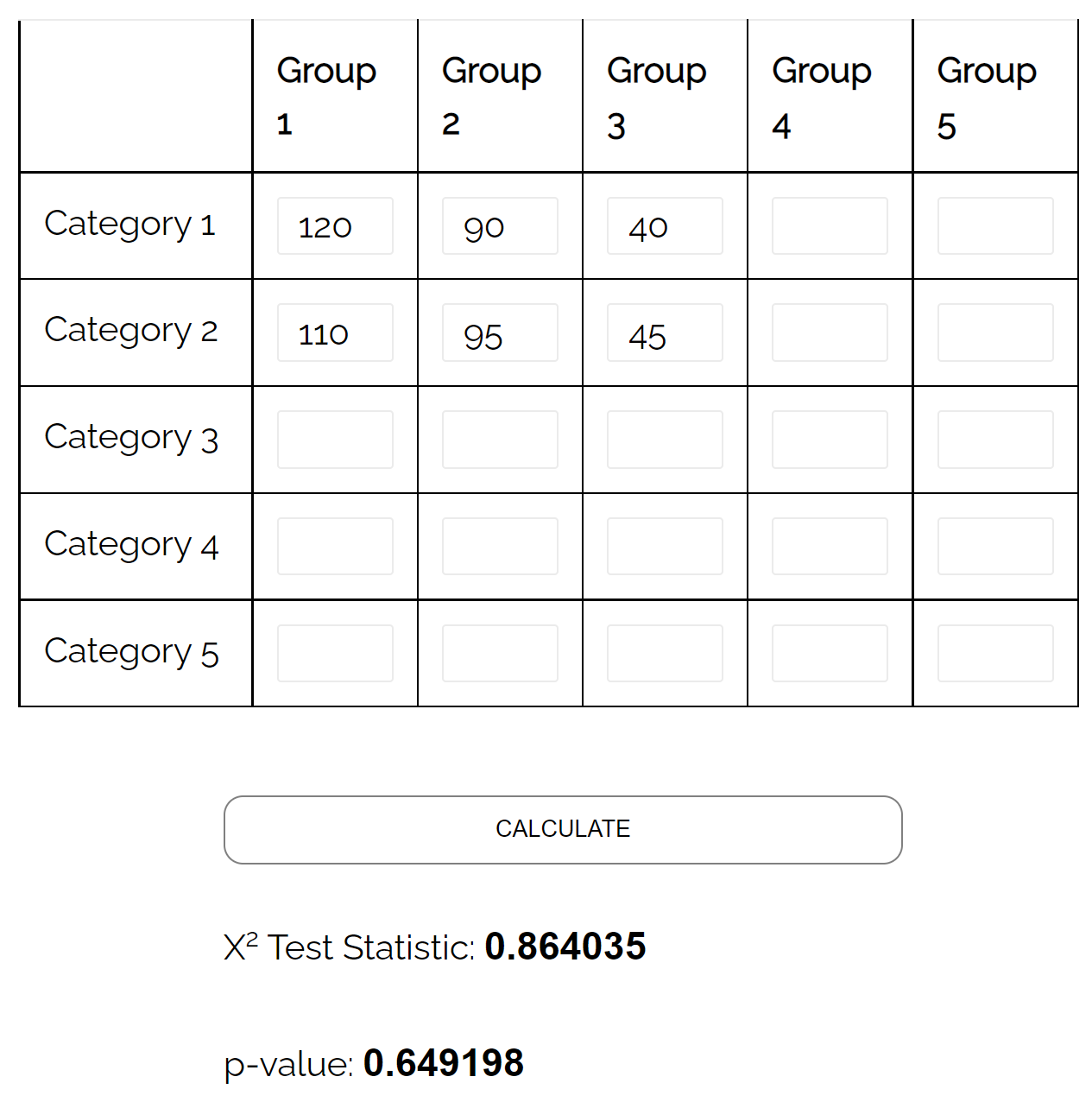
Karena nilai p ini tidak kurang dari 0,05, kami tidak memiliki cukup bukti untuk mengatakan bahwa terdapat hubungan antara gender dan preferensi partai politik.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan uji independensi chi-kuadrat menggunakan perangkat lunak statistik yang berbeda:
Pengantar Tes Kemerdekaan Chi-Kuadrat
Cara Melakukan Tes Independensi Chi-Kuadrat di Excel
Cara melakukan uji independensi chi-kuadrat di R
Kalkulator kemandirian uji chi-kuadrat