Rumus statistik

Oleh Benjamin anderson Agustus 1, 2023 Statistik 0 Komentar

Di sini Anda akan menemukan rumus statistik utama. Kami juga meninggalkan Anda tertaut ke artikel kami di mana Anda dapat melihat contoh penerapan setiap rumus statistik dan, selain itu, Anda dapat menggunakan kalkulator online sehingga tidak perlu melakukan perhitungan dan mengetahui hasil rumus secara langsung.

Rumus ukuran statistik tendensi sentral

Setengah

Untuk menghitung rata-rata, jumlahkan semua nilai lalu bagi dengan jumlah total data. Oleh karena itu, rumus rata-ratanya adalah sebagai berikut:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

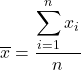
Dalam statistika, mean disebut juga dengan mean aritmatika atau rata-rata .

➤ Lihat: Kalkulator Rata-rata Aritmatika

median

Median adalah nilai tengah dari seluruh data yang diurutkan dari yang terkecil hingga yang terbesar. Dengan kata lain, median membagi kumpulan data yang diurutkan menjadi dua bagian yang sama besar.

Penghitungan median bergantung pada apakah jumlah datanya genap atau ganjil:

Jika jumlah seluruh data ganjil , maka median adalah nilai yang berada tepat di tengah-tengah data. Artinya nilai yang berada pada posisi (n+1)/2 dari data yang diurutkan.

$Me=x_{\frac{n+1}{2}$

Jika jumlah titik datanya genap , mediannya adalah rata-rata dua titik data yang terletak di tengah. Artinya rata-rata aritmatika dari nilai-nilai yang terdapat pada posisi n/2 dan n/2+1 dari data yang diurutkan.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Emas

$n$

adalah jumlah total data dalam sampel dan simbol Me menunjukkan median.

➤ Lihat: Kalkulator median

Mode

Dalam statistik, modus adalah nilai dalam kumpulan data yang mempunyai frekuensi absolut tertinggi, yaitu modus adalah nilai yang paling sering diulang dalam suatu kumpulan data.

Oleh karena itu, tidak ada rumus khusus untuk modus, tetapi untuk menghitung modus dari kumpulan data statistik, cukup hitung berapa kali setiap elemen data muncul dalam sampel, dan data yang paling sering diulang adalah modusnya.

Modusnya juga dapat dikatakan sebagai modus statistik atau nilai modal .

➤ Lihat: Kalkulator mode

Rumus ukuran statistik penyebaran

Deviasi standar

Deviasi standar, disebut juga deviasi standar, sama dengan akar kuadrat dari jumlah kuadrat deviasi rangkaian data dibagi dengan jumlah observasi.

Oleh karena itu, rumus simpangan baku adalah:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Lihat: Kalkulator deviasi standar

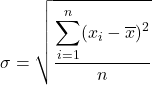
Perbedaan

Variansnya sama dengan jumlah kuadrat residu terhadap jumlah observasi. Oleh karena itu, rumus untuk metrik statistik ini adalah sebagai berikut:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Emas:

$X$

adalah variabel acak yang ingin Anda hitung variansnya.
$x_i$

adalah nilai datanya

$i$

.
$n$

adalah jumlah total pengamatan.
$\overline{X}$

adalah mean dari variabel acak

$X$

.

➤ Lihat: Kalkulator kesenjangan

Koefisien variasi

Dalam statistik, koefisien variasi adalah ukuran penyebaran yang digunakan untuk menentukan penyebaran suatu kumpulan data relatif terhadap rata-ratanya. Koefisien variasi dihitung dengan membagi simpangan baku data dengan rata-ratanya, kemudian dikalikan dengan 100 untuk menyatakan nilainya dalam persentase.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Lihat: Kalkulator koefisien variasi

Rapi

Rentang statistik adalah ukuran penyebaran yang menunjukkan perbedaan antara nilai maksimum dan nilai minimum data dalam suatu sampel. Oleh karena itu, untuk menghitung luas suatu populasi atau sampel statistik, nilai maksimum harus dikurangkan dari nilai minimum.

$R=\text{M\'ax}-\text{M\'in}$

➤ Lihat: Contoh rentang statistik

Jarak interkuartil

Rentang antarkuartil , disebut juga rentang antarkuartil , adalah ukuran penyebaran statistik yang menunjukkan perbedaan antara kuartil ketiga dan pertama.

Oleh karena itu, untuk menghitung rentang antarkuartil suatu kumpulan data statistik, Anda harus mencari kuartil ketiga dan pertama terlebih dahulu, lalu mengurangkannya.

$IQR=Q_3-Q_1$

➤ Lihat: Kalkulator Rentang Interkuartil

perbedaan sedang

Deviasi rata-rata , juga disebut deviasi absolut rata-rata , adalah rata-rata dari deviasi absolut. Oleh karena itu, simpangan rata-rata sama dengan jumlah simpangan setiap item data dari rata-rata aritmatika dibagi dengan jumlah total item data.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Lihat: Kalkulator deviasi rata-rata

Rumus pengukuran posisi statistik

kuartil

Dalam statistik, kuartil adalah tiga nilai yang membagi sekumpulan data terurut menjadi empat bagian yang sama besar. Jadi, kuartil pertama, kedua, dan ketiga masing-masing mewakili 25%, 50%, dan 75% dari seluruh data statistik.

Kuartil diwakili oleh huruf kapital Q dan indeks kuartil, sehingga kuartil pertama adalah Q ₁ , kuartil kedua adalah Q ₂ , dan kuartil ketiga adalah Q ₃ .

Rumus kuartilnya adalah:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Harap diperhatikan: rumus ini memberitahu kita posisi kuartil, bukan nilai kuartil. Kuartil adalah data yang terletak pada posisi yang diperoleh rumus.

Namun, terkadang hasil rumus ini memberi kita angka desimal. Oleh karena itu kita harus membedakan dua kasus tergantung pada apakah hasilnya berupa bilangan desimal atau bukan:

Jika hasil rumusnya berupa bilangan tanpa bagian desimal , maka kuartil adalah data yang posisinya disediakan oleh rumus di atas.
Jika hasil rumusnya berupa bilangan dengan bagian desimal , maka nilai kuartil dihitung menggunakan rumus berikut:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

➤ Lihat: Kalkulator Kuartil

desil

Dalam statistik, desil adalah sembilan nilai yang membagi sekumpulan data terurut menjadi sepuluh bagian yang sama. Sehingga desil pertama, kedua, ketiga,… mewakili 10%, 20%, 30%,… dari sampel atau populasi.

Desil diwakili oleh huruf kapital D dan indeks desil, yaitu desil pertama adalah D ₁ , desil kedua adalah D ₂ , desil ketiga adalah D ₃ , dan seterusnya.

Rumus desilnya adalah sebagai berikut:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Harap diperhatikan: rumus ini memberitahu kita posisi desil, bukan nilai desil. Desil adalah data yang terletak pada posisi yang diperoleh rumus.

Namun terkadang hasil rumus ini akan memberikan kita angka desimal, oleh karena itu kita harus membedakan dua kasus tergantung apakah hasilnya berupa angka desimal atau bukan:

Jika hasil rumusnya berupa bilangan tanpa bagian desimal , maka desil adalah data yang terletak pada posisi yang disediakan rumus di atas.
Jika hasil rumusnya berupa bilangan dengan bagian desimal , maka nilai desilnya dihitung menggunakan rumus berikut:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

➤ Lihat: Kalkulator desil

persentil

Dalam statistik, persentil adalah nilai yang membagi sekumpulan data terurut menjadi seratus bagian yang sama. Jadi, persentil menunjukkan nilai di bawah persentase kumpulan data.

Persentil dilambangkan dengan huruf kapital P dan indeks persentil, yaitu persentil pertama adalah P ₁ , persentil ke-40 adalah P ₄₀ , persentil ke-79 adalah P ₇₉ , dan seterusnya.

Rumus persentilnya adalah:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Harap diperhatikan: rumus ini memberi tahu kita posisi persentil, tetapi tidak menunjukkan nilainya. Persentilnya adalah data yang terletak pada posisi yang diperoleh rumus.

Namun terkadang hasil rumus ini akan memberikan kita angka desimal, oleh karena itu kita harus membedakan dua kasus tergantung apakah hasilnya berupa angka desimal atau bukan:

Jika hasil rumusnya berupa angka tanpa bagian desimal , maka persentilnya sesuai dengan data yang berada pada posisi yang disediakan rumus di atas.
Jika hasil rumusnya berupa angka dengan bagian desimal , maka nilai persentil pastinya dihitung menggunakan rumus berikut:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

➤ Lihat: Kalkulator Persentil

Rumus pengukuran bentuk statistik

koefisien asimetri

Koefisien skewness, atau indeks skewness, adalah koefisien statistik yang digunakan untuk menentukan skewness suatu distribusi. Jadi, dengan menghitung koefisien asimetri, Anda dapat mengetahui jenis asimetri distribusi tanpa harus membuat representasi grafisnya.

Rumus koefisien asimetri adalah sebagai berikut:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Dengan cara yang sama, salah satu dari dua rumus berikut dapat digunakan untuk menghitung koefisien asimetri Fisher:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

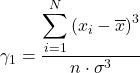
Emas

$E$

adalah ekspektasi matematis,

$\overline{x}$

mean aritmatika,

$\sigma$

simpangan baku dan

$n$

jumlah total data.

➤ Lihat: Koefisien asimetri

koefisien kurtosis

Kurtosis, juga disebut ketajaman, menunjukkan seberapa terkonsentrasi suatu distribusi di sekitar meannya. Dengan kata lain, kurtosis menunjukkan apakah suatu distribusi curam atau datar. Secara khusus, semakin besar kurtosis suatu distribusi, semakin curam (atau tajam) distribusi tersebut.

Rumus koefisien kurtosis adalah sebagai berikut:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

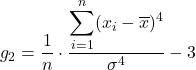
Emas

$x_i$

adalah nilai yang sesuai dengan observasi

$i$

$\overline{x}$

mean aritmatika,

$\sigma$

simpangan baku dan

$n$

jumlah total data.

➤ Lihat: Kalkulator Koefisien Perataan

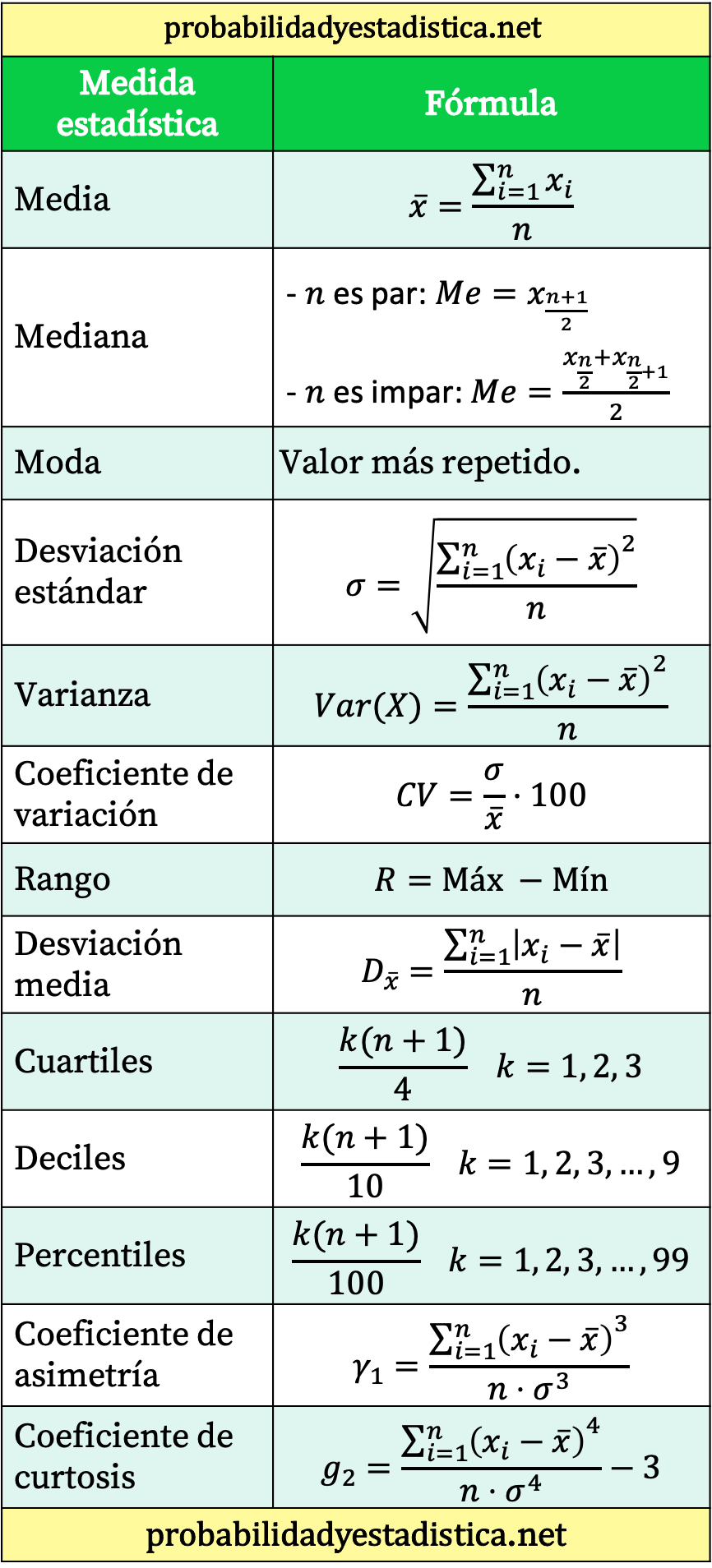
Tabel ringkasan semua rumus statistik

Terakhir, kami memberikan Anda tabel yang merangkum rumus statistik utama.

➤ Lihat: Rumus probabilitas

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Rumus ukuran statistik tendensi sentral

Setengah

median

Mode

Rumus ukuran statistik penyebaran

Deviasi standar

Perbedaan

Koefisien variasi

Rapi

Jarak interkuartil

perbedaan sedang

Rumus pengukuran posisi statistik

kuartil

desil

persentil

Rumus pengukuran bentuk statistik

koefisien asimetri

koefisien kurtosis

Tabel ringkasan semua rumus statistik

Tentang Penulis

Benjamin anderson

Tambahkan komentar