Cara melakukan uji-t satu sampel di sas

Uji-t satu sampel digunakan untuk menentukan apakah rata-rata populasi sama dengan nilai tertentu atau tidak.

Tutorial ini menjelaskan cara melakukan uji-t satu sampel di SAS.

Contoh: uji-t sampel di SAS

Misalkan seorang ahli botani ingin mengetahui apakah tinggi rata-rata suatu spesies tumbuhan tertentu sama dengan 15 inci. Dia mengambil sampel acak dari 12 tanaman dan mencatat tinggi masing-masing tanaman dalam inci.

Ketinggiannya adalah: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14

Gunakan langkah-langkah berikut untuk melakukan uji-t satu sampel untuk menentukan apakah tinggi rata-rata spesies tanaman ini sebenarnya 15 inci.

Langkah 1: Buat datanya.

Pertama, kita akan menggunakan kode berikut untuk membuat dataset di SAS:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

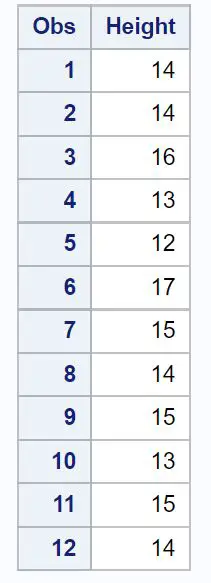
Langkah 2: Lakukan uji-t satu sampel.

Selanjutnya, kita akan menggunakan proc ttest untuk melakukan uji-t pada contoh:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

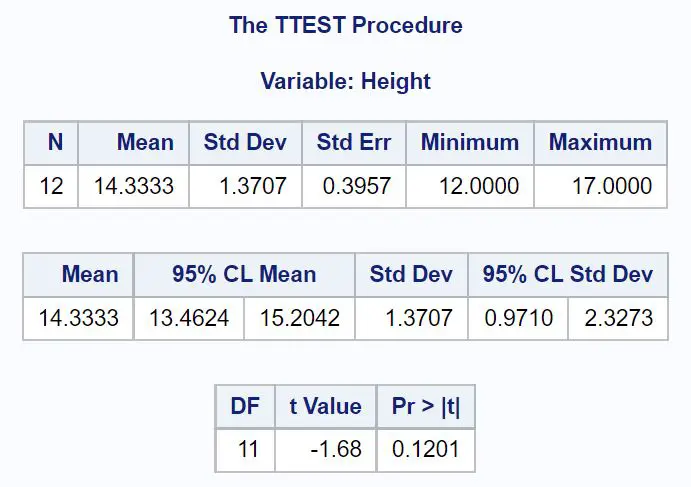
Tabel pertama menampilkan statistik deskriptif untuk sampel kami, termasuk:

• N (jumlah pengamatan): 12
• Rata-rata (rata-rata sampel): 14,3333
• Std Dev (sampel standar deviasi): 1,3707
• Kesalahan standar (kesalahan standar, dihitung sebagai s/ √n ): 0,3957
• Minimum (nilai minimum): 12
• Maksimum (nilai maksimum) 17

Tabel kedua menampilkan interval kepercayaan 95% untuk rata-rata populasi sebenarnya:

• 95% CI untuk μ: [13.4624, 15.2042]

Tabel ketiga menampilkan statistik uji-t dan nilai p yang sesuai:

• statistik uji-t: -1,68
• nilai p: 0,1201

Catatan : Statistik uji dihitung sebagai berikut:

• statistik uji t = ( x – μ) / (s/ √n )
• Statistik uji-t = (14.3333-15) / (1.3707/√ 12 )
• statistik uji-t = -1,68

Ingatlah bahwa uji-t satu sampel menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : μ = 15 inci
• _HA : μ ≠ 15 inci

Karena nilai p ( 0,1201 ) tidak kurang dari 0,05, kita gagal menolak hipotesis nol.

Ini berarti kita tidak memiliki cukup bukti untuk mengatakan bahwa tinggi rata-rata beberapa spesies tanaman berbeda dari 15 inci.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan uji statistik umum lainnya di SAS:

Cara melakukan tes peringkat bertanda Wilcoxon di SAS
Cara melakukan ANOVA satu arah di SAS