Cara melakukan uji-t satu sampel di spss

Uji-t satu sampel digunakan untuk menguji apakah rata-rata suatu populasi sama dengan nilai tertentu atau tidak.

Tutorial ini menjelaskan cara melakukan uji-t satu sampel di SPSS.

Contoh: Uji t satu sampel di SPSS

Seorang ahli botani ingin mengetahui apakah tinggi rata-rata suatu spesies tumbuhan tertentu sama dengan 15 inci. Dia mengambil sampel acak dari 12 tanaman dan mencatat tinggi masing-masing tanaman dalam inci:

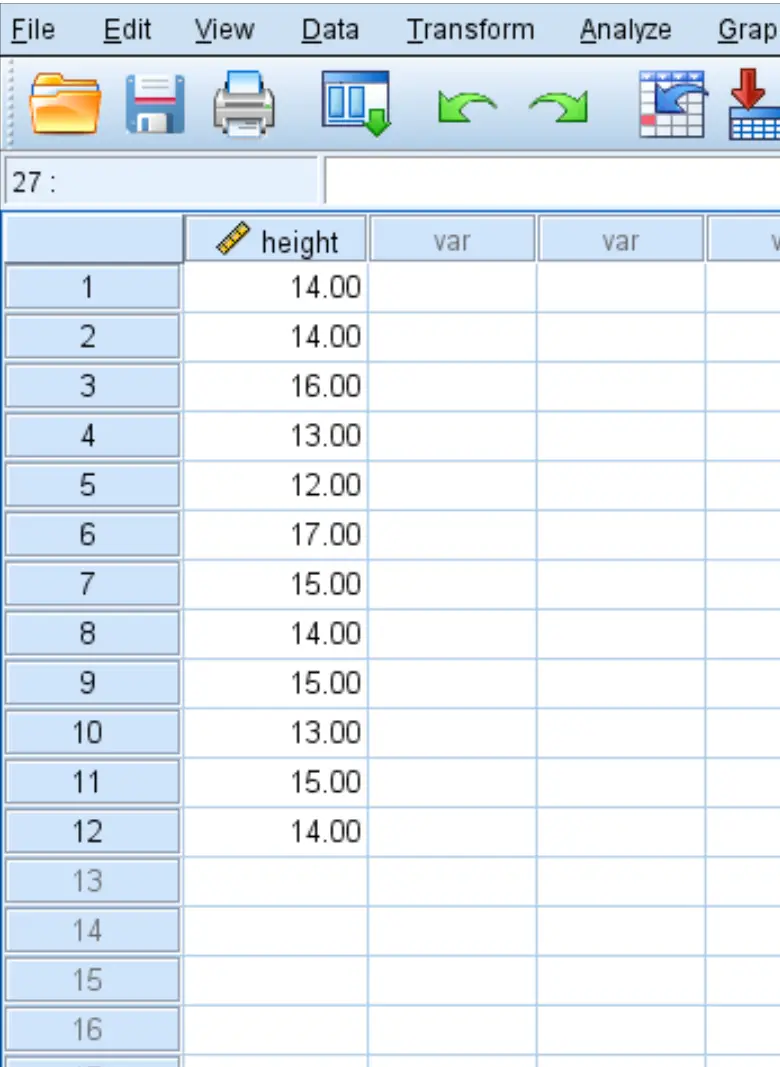
Gunakan langkah-langkah berikut untuk melakukan uji-t satu sampel untuk menentukan apakah tinggi rata-rata sebenarnya spesies tanaman ini sama dengan 15 inci, berdasarkan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : μ = 15 (rata-rata populasi sebenarnya sama dengan 15 inci)
• H ₁ : μ ≠ 15 (rata-rata populasi sebenarnya tidak sama dengan 15 inci)

Gunakan tingkat signifikansi α = 0,05.

Langkah 1: Pilih opsi uji-t satu sampel.

Klik tab Analyze , lalu Compare Means , lalu One-Sample T Test :

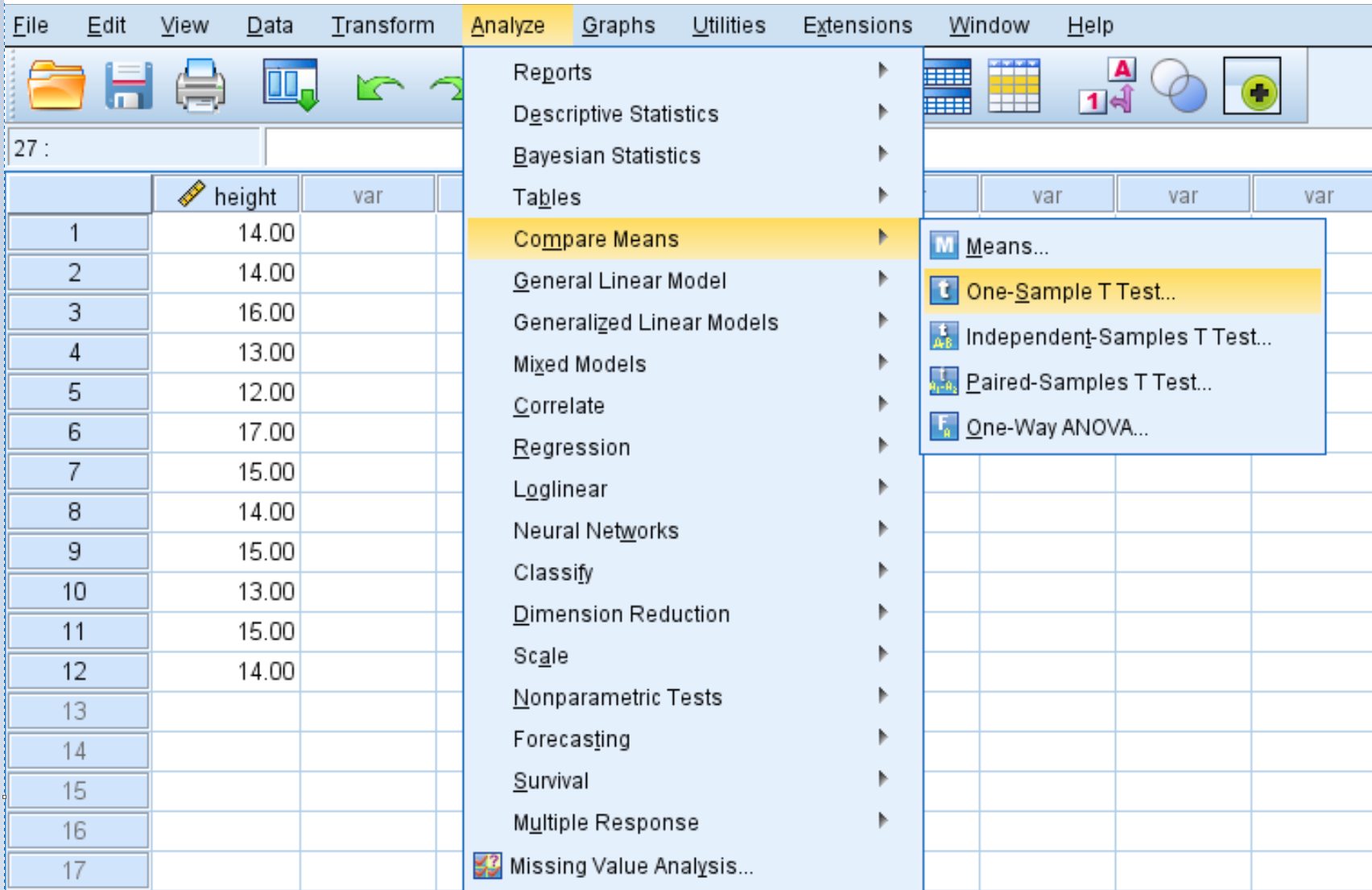
Langkah 2: Isikan nilai yang diperlukan untuk melakukan uji-t satu sampel.

Setelah Anda mengklik One-Sample T Test , jendela berikut akan muncul:

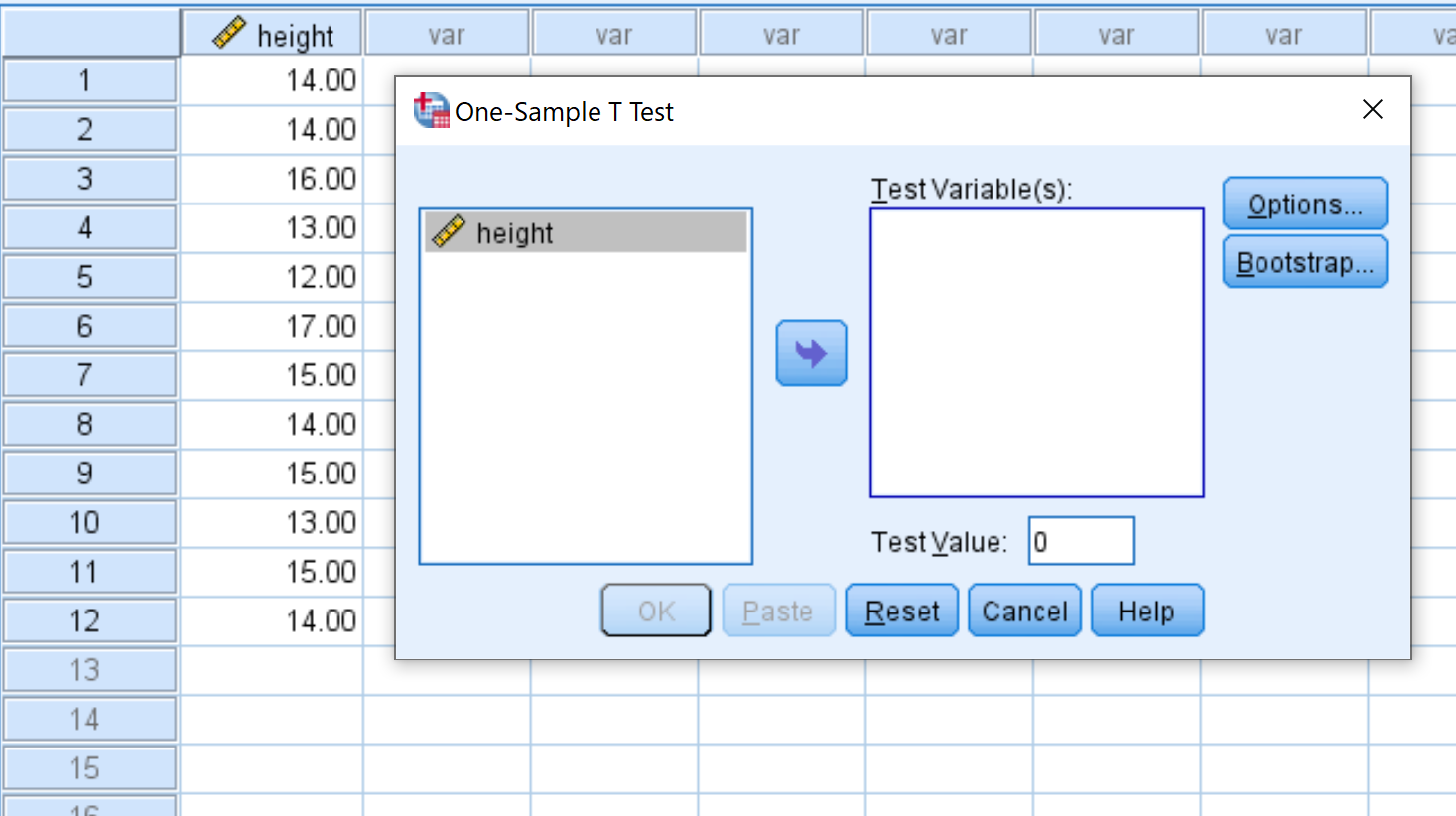
Seret tinggi variabel ke dalam kotak berlabel Test Variable(s) dan ubah Test Value menjadi 15. Lalu klik OK .

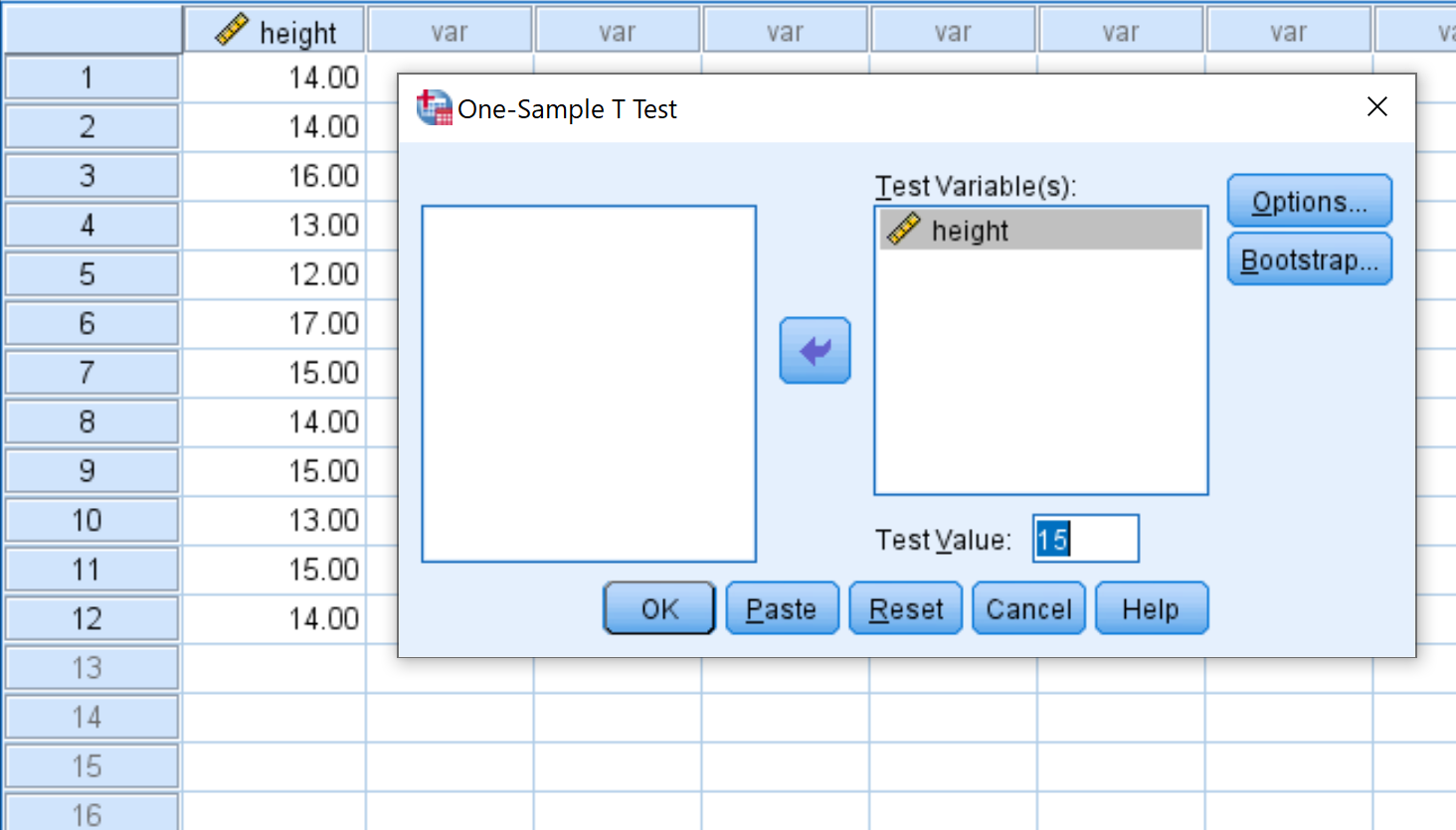
Langkah 3: Interpretasikan hasilnya.

Setelah Anda mengklik OK , hasil uji-t satu sampel akan ditampilkan:

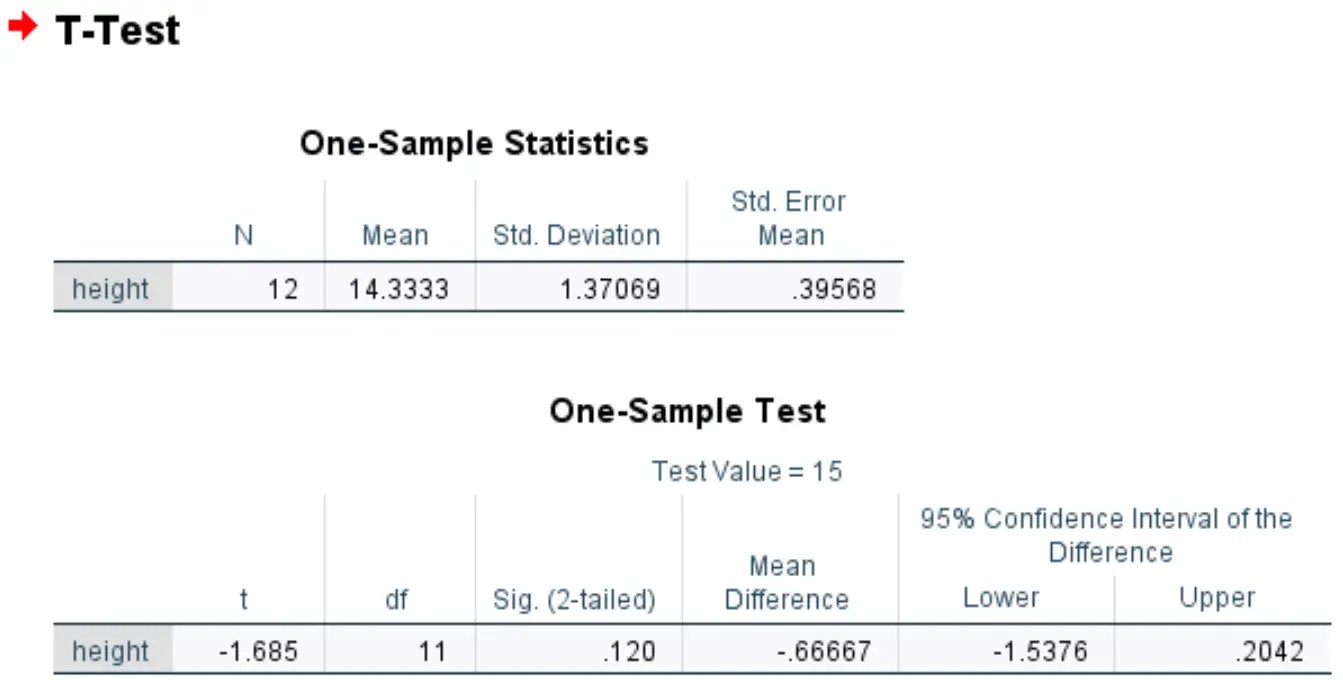
Tabel pertama menampilkan ringkasan statistik untuk tinggi variabel:

• N: Ukuran sampel
• Rata-rata: rata-rata tinggi tanaman dalam sampel
• Standar. Deviasi : Standar deviasi tinggi tanaman dalam sampel.
• Standar. Kesalahan rata-rata: kesalahan standar rata-rata, dihitung sebagai s/√n

Tabel kedua menampilkan hasil uji t satu sampel:

• t: Statistik uji, dihitung sebagai (x – μ) / (s/√n) = (14.3333-15) / (1.37/√12) = -1.685
• df: Derajat kebebasan, dihitung n-1 = 12-1 = 11
• tanda tangan. (dua sisi): Nilai p dua sisi yang sesuai dengan nilai -1,685 dengan df=11
• Perbedaan rata-rata: perbedaan antara rata-rata sampel dan rata-rata hipotetis
• Perbedaan CI 95%: Interval kepercayaan 95% untuk perbedaan sebenarnya antara mean sampel dan mean hipotetis.

Karena nilai p tes (0,120) tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa tinggi rata-rata sebenarnya dari spesies tanaman ini selain 15 inci.