Kuadrat terkecil parsial dengan python (langkah demi langkah)

Salah satu masalah paling umum yang akan Anda temui dalam pembelajaran mesin adalah multikolinearitas . Hal ini terjadi ketika dua atau lebih variabel prediktor dalam kumpulan data berkorelasi tinggi.

Jika hal ini terjadi, suatu model mungkin dapat menyesuaikan dengan kumpulan data pelatihan dengan baik, namun model tersebut mungkin memiliki performa yang buruk pada kumpulan data baru yang belum pernah dilihatnya karena model tersebut terlalu cocok dengan kumpulan data pelatihan. perlengkapan latihan.

Salah satu cara untuk mengatasi masalah ini adalah dengan menggunakan metode yang disebut kuadrat terkecil parsial , yang cara kerjanya sebagai berikut:

• Standarisasi variabel prediktor dan respons.
• Hitung M kombinasi linier (disebut “komponen PLS”) dari p variabel prediktor asli yang menjelaskan sejumlah besar variasi baik dalam variabel respons maupun variabel prediktor.
• Gunakan metode kuadrat terkecil untuk menyesuaikan model regresi linier menggunakan komponen PLS sebagai prediktor.
• Gunakan validasi silang k-fold untuk menemukan jumlah komponen PLS yang optimal untuk dipertahankan dalam model.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan kuadrat terkecil parsial dengan Python.

Langkah 1: Impor paket yang diperlukan

Pertama, kita akan mengimpor paket yang diperlukan untuk melakukan kuadrat terkecil parsial dengan Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Langkah 2: Muat data

Untuk contoh ini, kita akan menggunakan kumpulan data bernama mtcars , yang berisi informasi tentang 33 mobil berbeda. Kita akan menggunakan hp sebagai variabel respon dan variabel berikut sebagai prediktor:

• mpg
• menampilkan
• kotoran
• berat
• qdetik

Kode berikut menunjukkan cara memuat dan menampilkan kumpulan data ini:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Langkah 3: Pasangkan model kuadrat terkecil parsial

Kode berikut menunjukkan cara menyesuaikan model PLS dengan data ini.

Perhatikan bahwa cv = RepeatedKFold() memberitahu Python untuk menggunakan validasi silang k-fold untuk mengevaluasi kinerja model. Untuk contoh ini kita pilih k = 10 kali lipat, diulang sebanyak 3 kali.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

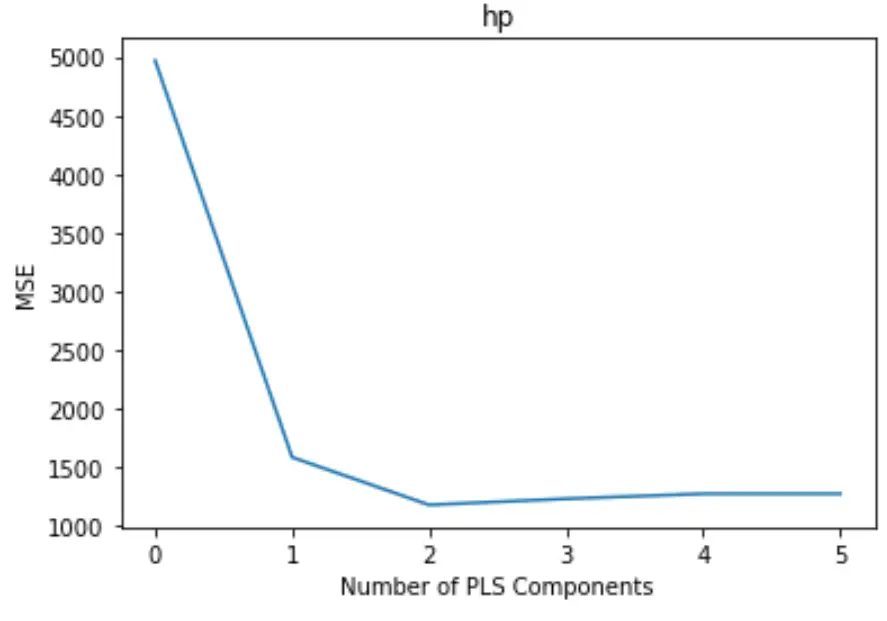
Plot menampilkan jumlah komponen PLS sepanjang sumbu x dan pengujian MSE (mean square error) sepanjang sumbu y.

Dari grafik tersebut, kita dapat melihat bahwa MSE pengujian menurun dengan menambahkan dua komponen PLS, namun mulai meningkat ketika kita menambahkan lebih dari dua komponen PLS.

Dengan demikian, model optimal hanya mencakup dua komponen PLS pertama.

Langkah 4: Gunakan model akhir untuk membuat prediksi

Kita dapat menggunakan model PLS final dengan dua komponen PLS untuk membuat prediksi tentang observasi baru.

Kode berikut menunjukkan cara membagi kumpulan data asli menjadi kumpulan pelatihan dan pengujian serta menggunakan model PLS dengan dua komponen PLS untuk membuat prediksi pada kumpulan pengujian.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Kita melihat RMSE tes tersebut ternyata 29.9094 . Ini adalah deviasi rata-rata antara nilai hp yang diprediksi dan nilai hp yang diamati untuk observasi set pengujian.

Kode Python lengkap yang digunakan dalam contoh ini dapat ditemukan di sini .