Bagaimana menafsirkan sig. nilai (dua sisi) di spss
Seringkali ketika Anda melakukan pengujian statistik di SPSS, tabel keluaran berisi Sig. nilai (bilateral) .
Nilai ini mewakili nilai p dua sisi dari pengujian.
Jika nilai ini berada di bawah tingkat signifikansi Anda (pilihan umum adalah 0,05 atau 0,01), maka Anda dapat menolak hipotesis nol pengujian Anda.
Tutorial ini memberikan contoh bagaimana menafsirkan Sig. (dua sisi) nilai uji statistik yang berbeda.
Contoh 1: Uji-t satu sampel
Uji-t satu sampel digunakan untuk menguji apakah rata-rata suatu populasi sama dengan nilai tertentu atau tidak.
Misalnya, seorang ahli botani ingin mengetahui apakah tinggi rata-rata suatu spesies tanaman tertentu sama dengan 15 inci. Dia mengambil sampel acak dari 12 tanaman dan mencatat tinggi masing-masing tanaman dalam inci.
Kemudian sampel ini digunakan untuk melakukan uji-t satu sampel dengan hipotesis nol dan hipotesis alternatif berikut:
- H 0 : μ = 15 (rata-rata populasi sebenarnya sama dengan 15 inci)
- H A : μ ≠ 15 (rata-rata populasi sebenarnya tidak sama dengan 15 inci)
Dia menjalankan uji-t satu sampel di SPSS dan mendapatkan hasil sebagai berikut:
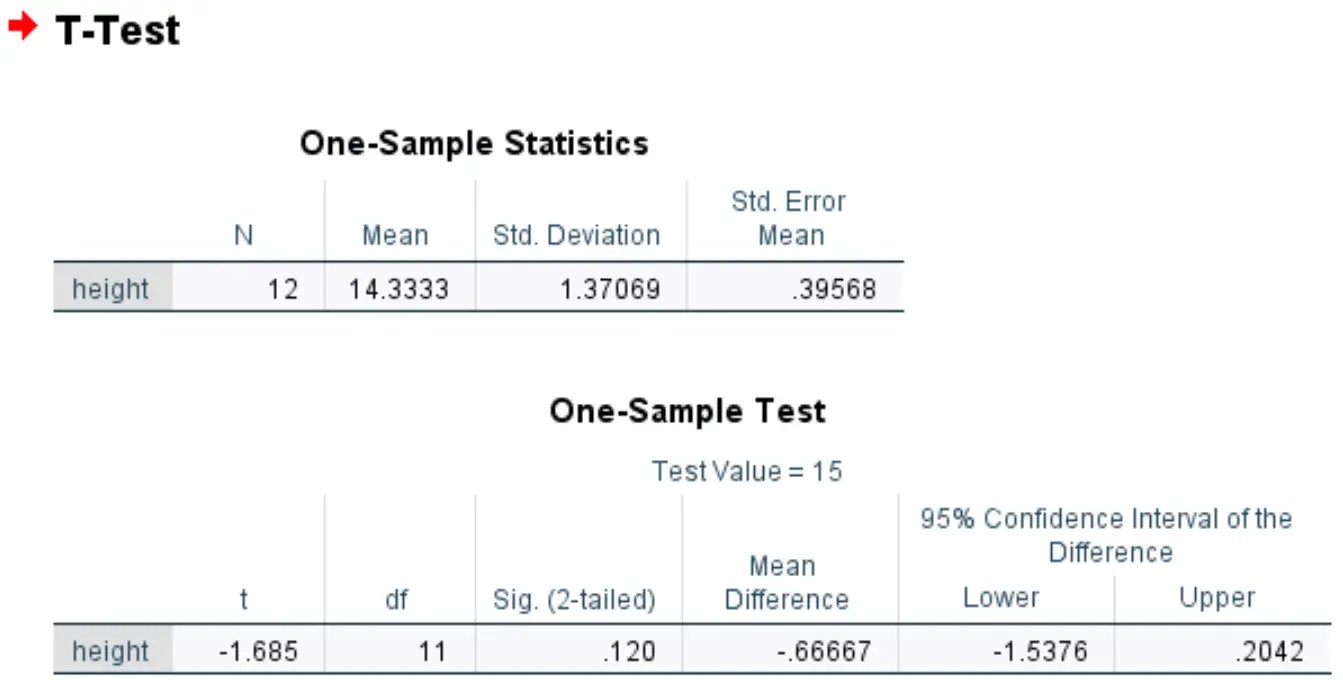
Tanda tangan itu. Nilainya (dua sisi) adalah 0,120 .
Ini mewakili nilai p dua sisi yang sesuai dengan nilai -1,685 dengan 11 derajat kebebasan.
Karena nilai p tes (0,120) tidak kurang dari 0,05, kita gagal menolak hipotesis nol.
Dengan kata lain, kita tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata tinggi sebenarnya spesies tanaman ini selain 15 inci.
Contoh 2: Uji-t dua sampel
Uji-t dua sampel digunakan untuk menguji apakah nilai rata-rata dua populasi sama atau tidak.
Misalnya, peneliti ingin mengetahui apakah perlakuan bahan bakar baru menyebabkan perubahan rata-rata jarak tempuh per galon mobil tertentu. Untuk mengujinya, mereka melakukan percobaan di mana 12 mobil menerima perlakuan bahan bakar baru dan 12 mobil tidak.
Peneliti melakukan uji-t dua sampel dengan hipotesis nol dan hipotesis alternatif berikut:
- H 0 : μ 1 = μ 2 (rata-rata mpg antara kedua populasi adalah sama)
- H 1 : μ 1 ≠ μ 2 (rata-rata mpg antara kedua populasi tidak sama)
Mereka melakukan uji-t dua sampel di SPSS dan memperoleh hasil sebagai berikut:
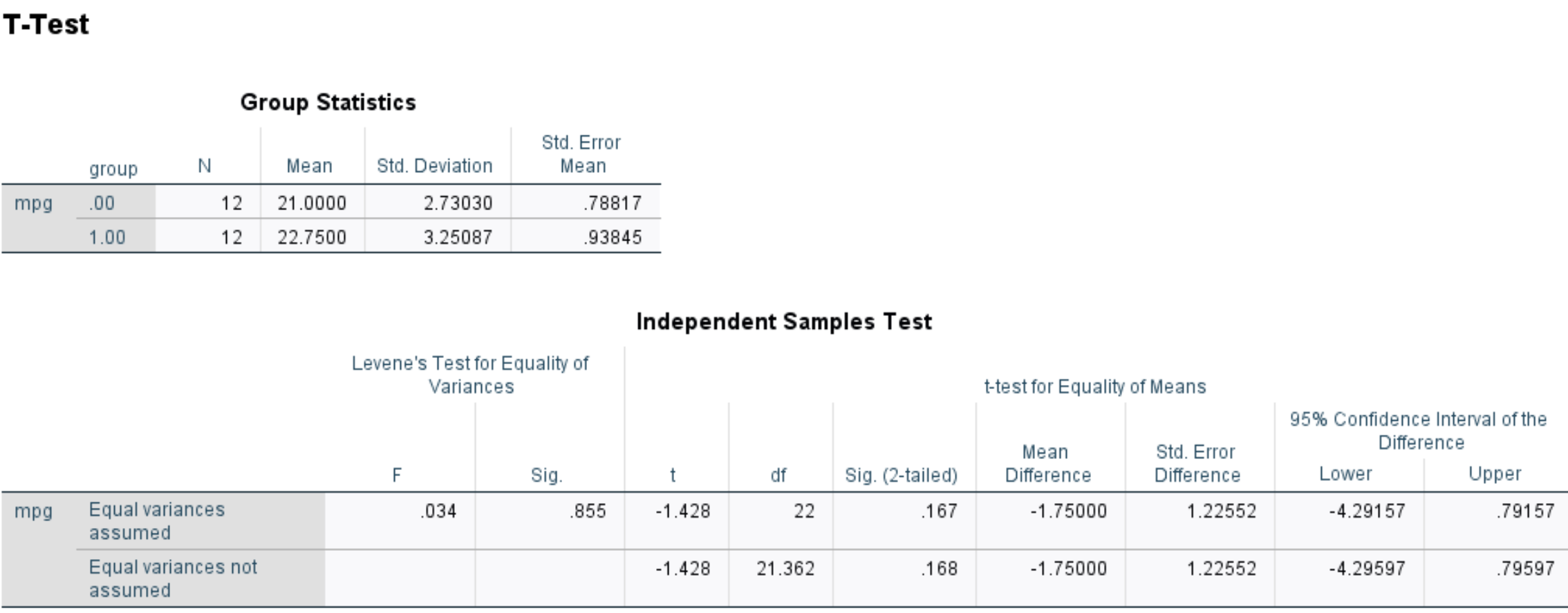
Tanda tangan itu. Nilainya (2 sisi) adalah 0,167 .
Ini mewakili nilai p dua sisi yang sesuai dengan nilai -1,428 dengan 22 derajat kebebasan.
Karena nilai p dari pengujian (0,167) tidak kurang dari 0,05, kami gagal menolak hipotesis nol.
Dengan kata lain, kita tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata mpg sebenarnya berbeda antara mobil yang mendapat perawatan dan yang tidak.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan berbagai uji statistik di SPSS:
Cara melakukan uji-t satu sampel di SPSS
Cara melakukan uji-t dua sampel di SPSS
Cara melakukan uji-t sampel berpasangan di SPSS
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya