T-score vs z-score: kapan menggunakannya?

Dua istilah yang sering membingungkan mahasiswa pada mata kuliah statistika adalah t-score dan z-score .

Keduanya banyak digunakan saat melakukan pengujian hipotesis atau membangun interval kepercayaan , namun keduanya sedikit berbeda.

Berikut rumus masing-masingnya:

skor t = ( x – μ) / (s/√ n )

Emas:

• x : mean sampel
• μ : Rata-rata populasi
• s : Contoh simpangan baku
• n : Ukuran sampel

skor-z = ( x – μ) / σ

Emas:

• x : Nilai data mentah
• μ : Rata-rata populasi
• σ : Simpangan baku populasi

Diagram alur ini menunjukkan kapan Anda harus menggunakan masing-masing, berdasarkan data Anda:

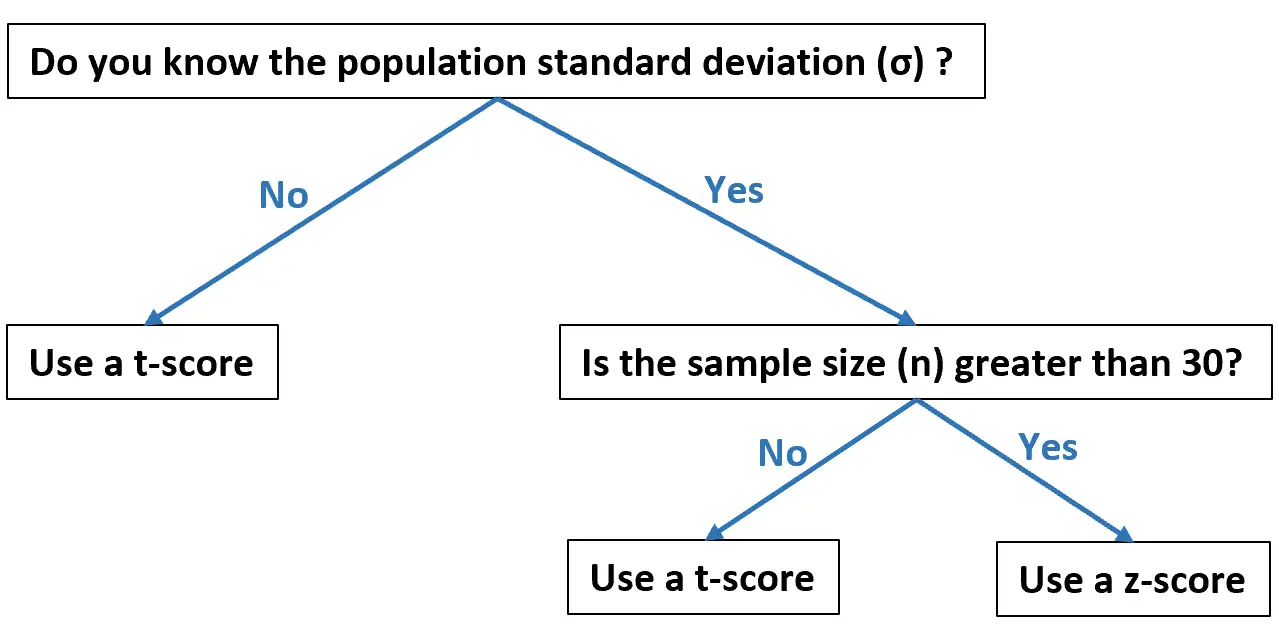
Contoh berikut menunjukkan cara menghitung T-score dan Z-score dalam praktiknya.

Contoh 1: Perhitungan T-Score

Misalkan sebuah restoran menyiapkan hamburger yang mengklaim memiliki berat rata-rata μ = 0,25 pon.

Misalkan kita mengambil sampel acak n = 20 hamburger dan menemukan bahwa berat rata-rata sampel adalah x = 0,22 pon dengan deviasi standar s = 0,05 pon. Lakukan uji hipotesis untuk menentukan apakah berat rata-rata sebenarnya dari semua hamburger yang diproduksi oleh restoran ini sama dengan 0,25 pon.

Untuk contoh ini, kita akan menggunakan skor-T untuk melakukan uji hipotesis karena tidak satu pun dari dua kondisi berikut ini yang terpenuhi.

• Simpangan baku populasi (σ) diketahui. (σ tidak disediakan dalam contoh ini)
• Ukuran sampel lebih besar dari 30. (n=20 dalam contoh ini)

Jadi, kita akan menghitung t-score sebagai berikut:

• skor t = ( x – μ) / (s/√ n )
• t-skor = (0,22 – 0,25) / (0,05 / √ 20 )
• t-skor = -2,68

Menurut kalkulator skor-T nilai-P , nilai-p yang sesuai dengan skor-t ini adalah 0,01481 .

Karena nilai p ini kurang dari 0,05, kami mempunyai cukup bukti untuk mengatakan bahwa berat rata-rata hamburger yang diproduksi di restoran ini tidak sama dengan 0,25 pon.

Contoh 2: Menghitung skor Z

Asumsikan sebuah perusahaan memproduksi baterai yang masa pakainya diketahui mengikuti distribusi normal dengan rata-rata μ = 20 jam dan deviasi standar σ = 5 jam.

Misalkan kita mengambil sampel acak n = 50 baterai dan menemukan bahwa rata-rata sampelnya adalah x = 21 jam. Lakukan uji hipotesis untuk menentukan apakah umur rata-rata sebenarnya dari semua baterai yang diproduksi oleh perusahaan ini sama dengan 20 jam.

Untuk contoh ini, kita akan menggunakan skor-z untuk melakukan uji hipotesis karena kedua kondisi berikut terpenuhi:

• Simpangan baku populasi (σ) diketahui. (σ sama dengan 5 dalam contoh ini)
• Ukuran sampel lebih besar dari 30. (n=50 dalam contoh ini)

Jadi, kami akan menghitung skor-z sebagai berikut:

• skor-z = ( x – μ) / σ
• skor-z = (21 – 20) / 5
• skor-z = 0,2

Menurut kalkulator skor-Z nilai-P, nilai-p yang sesuai dengan skor-z ini adalah 0,84184 .

Karena nilai p ini tidak kurang dari 0,05, kami tidak memiliki cukup bukti untuk mengatakan bahwa umur rata-rata semua baterai yang diproduksi oleh perusahaan ini berbeda dari 20 jam.

Sumber daya tambahan

Tutorial berikut menawarkan informasi lebih lanjut tentang skor T dan skor Z:

Distribusi normal vs distribusi t: apa bedanya?
Cara membaca tabel distribusi t
Cara membaca tabel Z