Bisakah z-score menjadi negatif?

Dalam statistik, skor-z memberi tahu kita berapa banyak standar deviasi suatu nilai dari mean . Kami menggunakan rumus berikut untuk menghitung skor-z:

z = (X – μ) / σ

dimana X adalah nilai yang kita analisis, μ adalah mean dan σ adalah standar deviasi.

Skor z bisa positif, negatif, atau nol.

Skor z yang positif menunjukkan bahwa suatu nilai tertentu berada di atas rata-rata, skor z yang negatif menunjukkan bahwa suatu nilai tertentu berada di bawah rata-rata, dan skor az yang nol menunjukkan bahwa suatu nilai tertentu sama dengan rata-rata.

Beberapa contoh akan memperjelas hal ini.

Contoh: Menghitung skor Z

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan tinggi (dalam inci) sekelompok tanaman tertentu:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

Rata-rata sampel kumpulan data ini adalah 13 dan deviasi standar sampel adalah 5,51 .

1. Temukan skor-z untuk nilai “8” dalam kumpulan data ini.

Berikut cara menghitung z-score:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Artinya nilai “8” adalah 0,91 standar deviasi lebih rendah dari mean.

2. Temukan skor-z untuk nilai “13” dalam kumpulan data ini.

Berikut cara menghitung z-score:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Artinya nilai “13” sama persis dengan rata-rata.

3. Temukan skor-z untuk nilai “20” dalam kumpulan data ini.

Berikut cara menghitung z-score:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Artinya nilai “20” berada 1,28 standar deviasi di atas mean.

Bagaimana menafsirkan skor Z

Bagan AZ memberi tahu kita berapa persentase nilai yang berada di bawah skor Z tertentu. Beberapa contoh akan memperjelas hal ini.

Contoh 1: Skor Z negatif

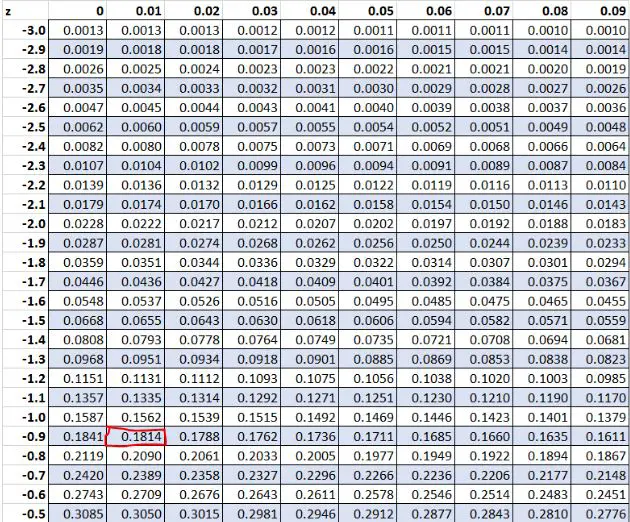
Sebelumnya, kami menemukan bahwa nilai mentah “8” dalam kumpulan data kami memiliki skor-z -0,91 . Berdasarkan tabel Z, 18,14% nilainya lebih rendah dari nilai ini.

Contoh 2: Z-Score sama dengan nol

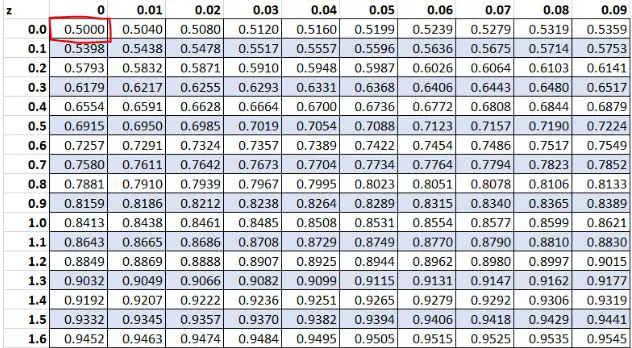
Sebelumnya, kami menemukan bahwa nilai mentah “13” dalam kumpulan data kami memiliki skor-z 0 . Menurut tabel Z, 50,00% nilainya kurang dari nilai ini.

Contoh 3: Skor Z positif

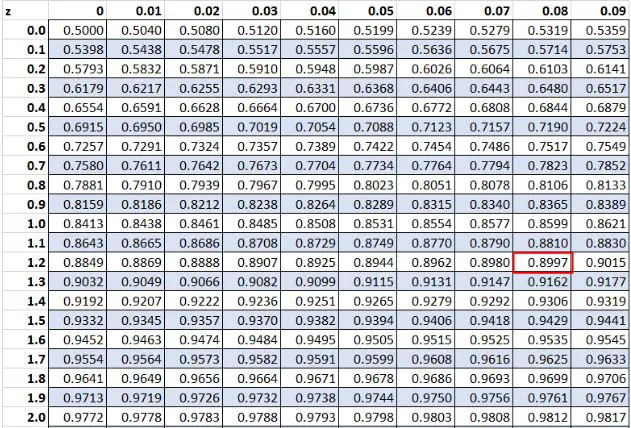
Sebelumnya, kami menemukan bahwa nilai mentah “20” dalam kumpulan data kami memiliki skor-z 1,28 . Berdasarkan tabel Z, 89,97% nilainya lebih rendah dari nilai tersebut.

Kesimpulan

Skor Z dapat mengambil nilai apa pun antara tak terhingga negatif dan tak terhingga positif, namun sebagian besar skor z berada dalam 2 standar deviasi dari mean. Sebenarnya ada aturan dalam statistik yang dikenal sebagai aturan praktis , yang menyatakan bahwa untuk kumpulan data tertentu yang berdistribusi normal:

• 68% nilai data berada dalam satu standar deviasi mean.
• 95% nilai data berada dalam dua standar deviasi dari mean.
• 99,7% nilai data berada dalam tiga standar deviasi mean.

Semakin tinggi nilai absolut skor-z, semakin jauh nilai mentahnya dari rata-rata kumpulan data. Semakin rendah nilai absolut skor-z, semakin dekat nilai mentahnya dengan rata-rata kumpulan data.

Topik-topik terkait:

Aturan Kalkulator Jempol
Bagaimana menerapkan aturan praktis di Excel