Cara melakukan regresi linier berganda di spss

Regresi linier berganda merupakan salah satu metode yang dapat kita gunakan untuk memahami hubungan antara dua atau lebih variabel penjelas dan suatu variabel respon.

Tutorial ini menjelaskan cara melakukan regresi linier berganda di SPSS.

Contoh: Regresi Linier Berganda di SPSS

Misalkan kita ingin mengetahui apakah jumlah jam yang dihabiskan untuk belajar dan jumlah ujian praktik yang diambil mempengaruhi nilai yang diterima siswa pada ujian tertentu. Untuk mengeksplorasi hal ini, kita dapat melakukan regresi linier berganda dengan menggunakan variabel berikut:

Variabel penjelas:

• Berjam-jam belajar
• Ujian persiapan berlalu

Variabel respon:

• Hasil ujian

Gunakan langkah-langkah berikut untuk melakukan regresi linier berganda di SPSS.

Langkah 1: Masukkan datanya.

Masukkan data jumlah jam belajar, ujian persiapan yang diambil, dan hasil ujian yang diterima untuk 20 siswa berikut ini:

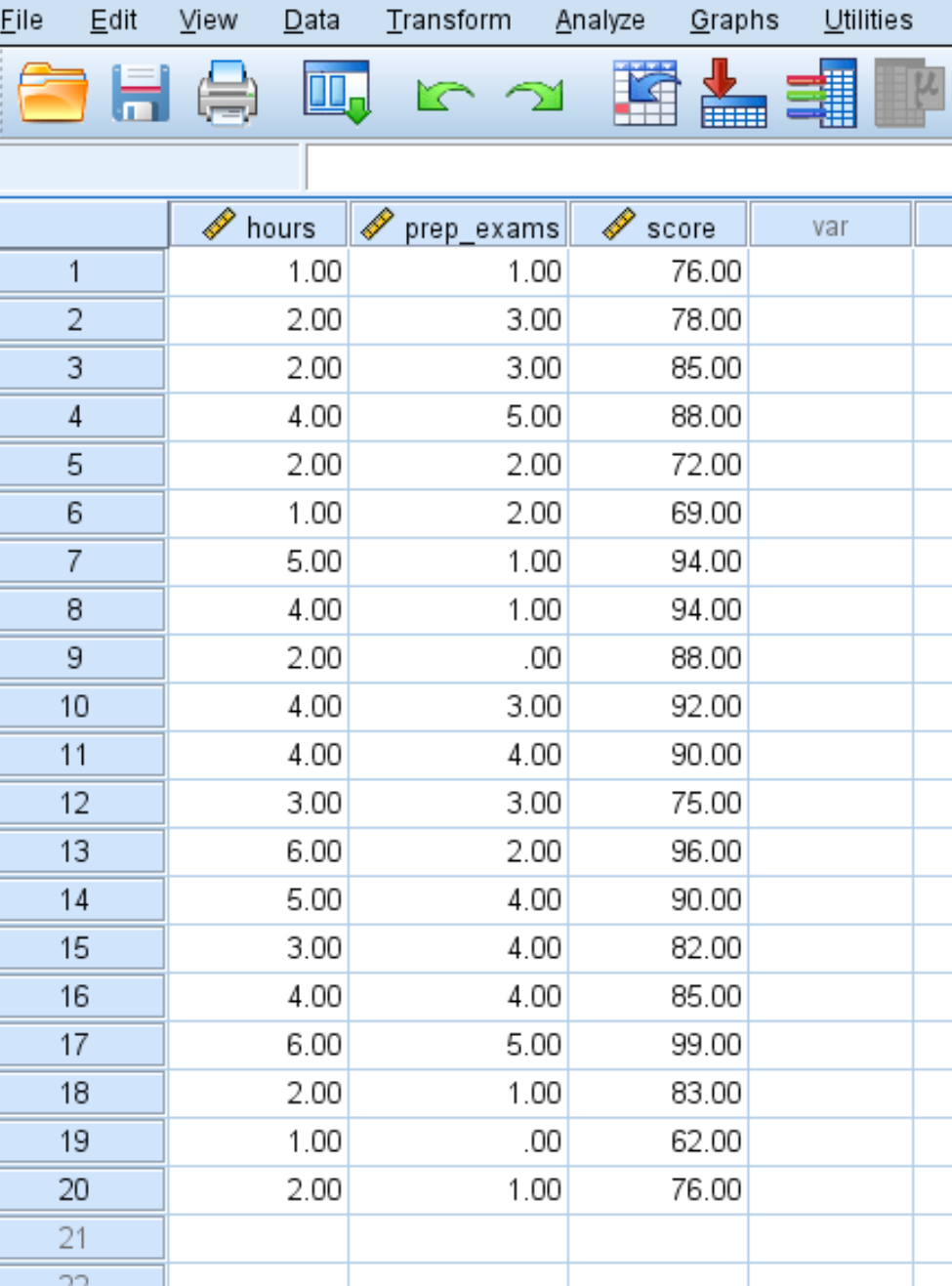
Langkah 2: Lakukan regresi linier berganda.

Klik tab Analisis , lalu Regresi , lalu Linear :

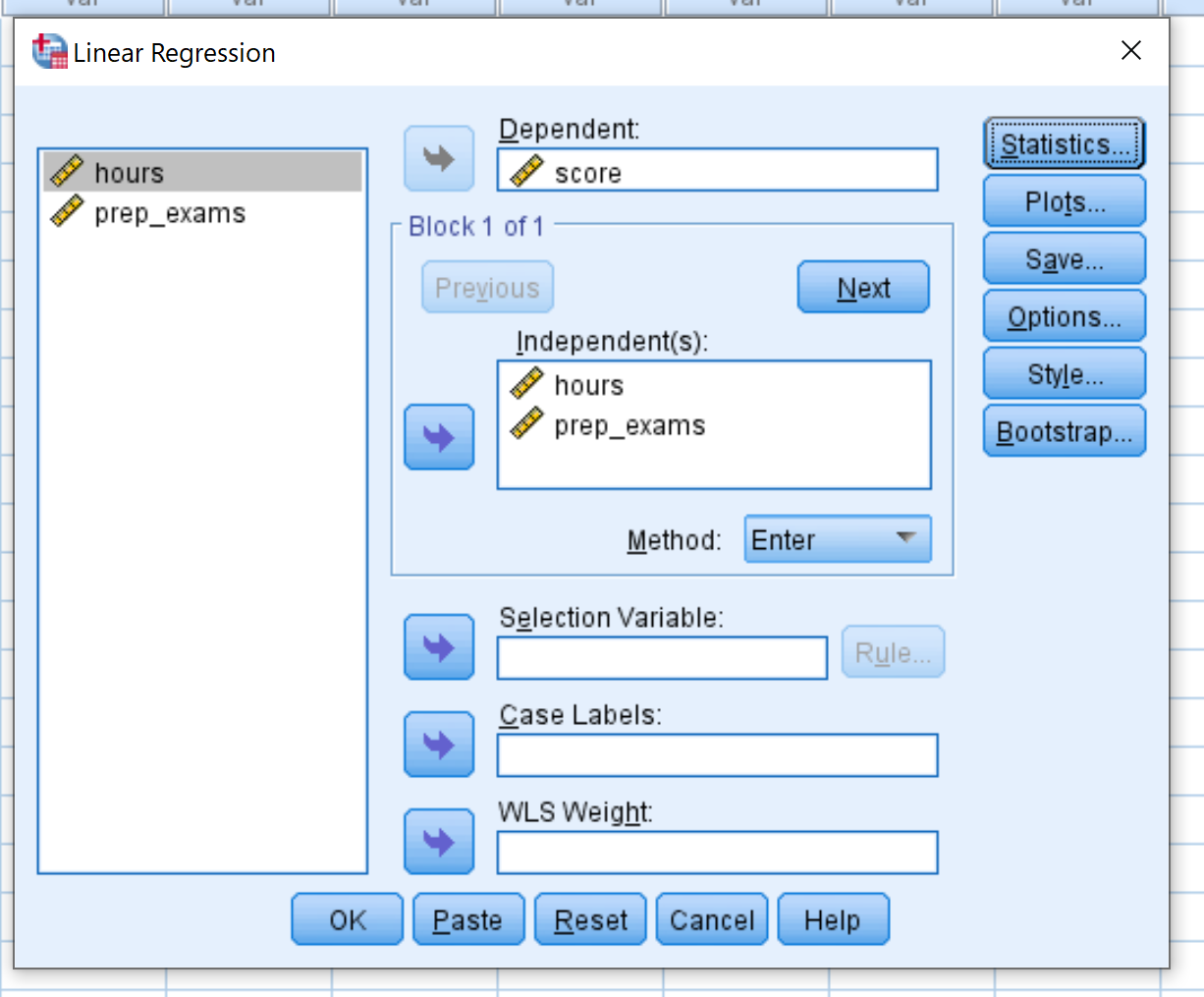
Tarik skor variabel ke dalam kotak berlabel Dependent. Seret variabel jam dan prep_exams ke dalam kotak berlabel Independen. Lalu klik oke .

Langkah 3: Tafsirkan hasilnya.

Setelah Anda mengklik OK , hasil regresi linier berganda akan muncul di jendela baru.

Tabel pertama yang menarik bagi kami disebut Ringkasan Model :

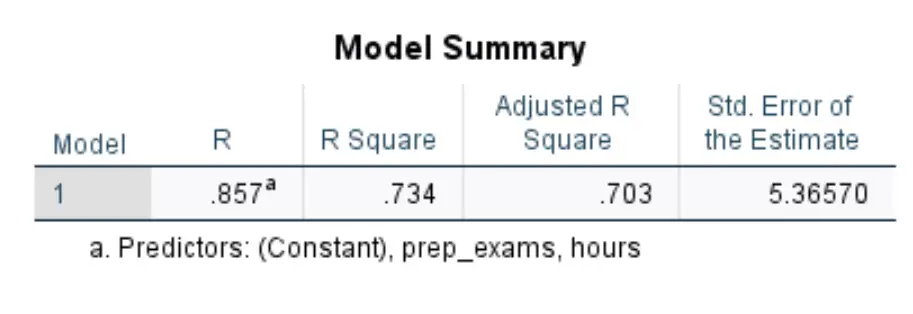
Berikut cara menafsirkan angka paling relevan dalam tabel ini:

• R Square : Merupakan proporsi varians variabel respon yang dapat dijelaskan oleh variabel penjelas. Dalam contoh ini, 73,4% variasi nilai ujian dapat dijelaskan oleh jam belajar dan jumlah persiapan ujian yang diambil.
• Standar. Kesalahan estimasi: kesalahan standar adalah jarak rata-rata antara nilai yang diamati dan garis regresi. Dalam contoh ini, nilai yang diamati rata-rata menyimpang sebesar 5,3657 unit dari garis regresi.

Tabel berikutnya yang menarik bagi kami disebut ANOVA :

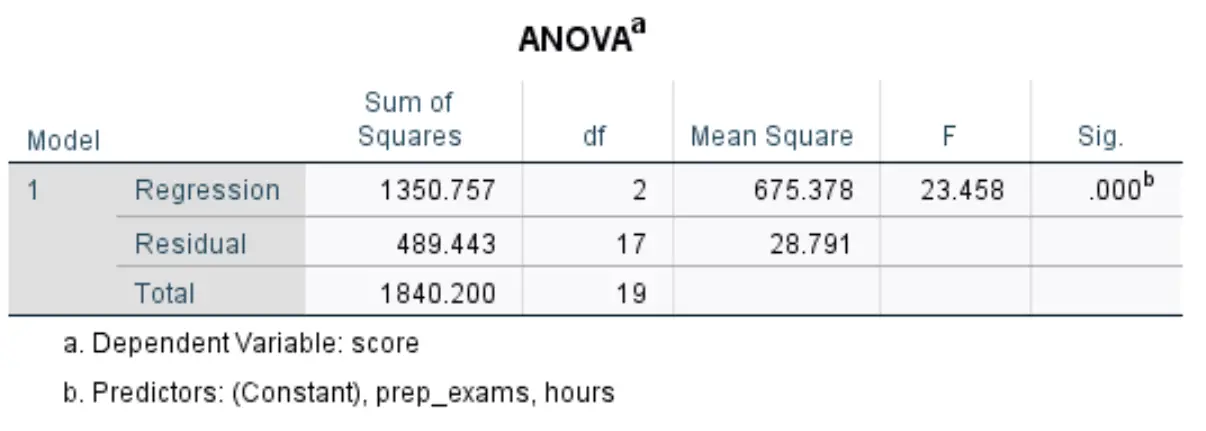
Berikut cara menafsirkan angka paling relevan dalam tabel ini:

• F: Ini adalah statistik F keseluruhan untuk model regresi, yang dihitung sebagai Mean Square Regression / Mean Square Residual.
• Sig: Ini adalah nilai p yang terkait dengan statistik F secara keseluruhan. Hal ini memberitahu kita apakah model regresi secara keseluruhan signifikan secara statistik atau tidak. Dengan kata lain, hal ini memberi tahu kita apakah gabungan dua variabel penjelas mempunyai hubungan yang signifikan secara statistik dengan variabel respons. Dalam hal ini, nilai p sama dengan 0,000, yang menunjukkan bahwa variabel penjelas, jam belajar dan persiapan ujian yang diambil, memiliki hubungan yang signifikan secara statistik dengan hasil ujian.

Tabel berikut yang menarik minat kami berjudul Koefisien :

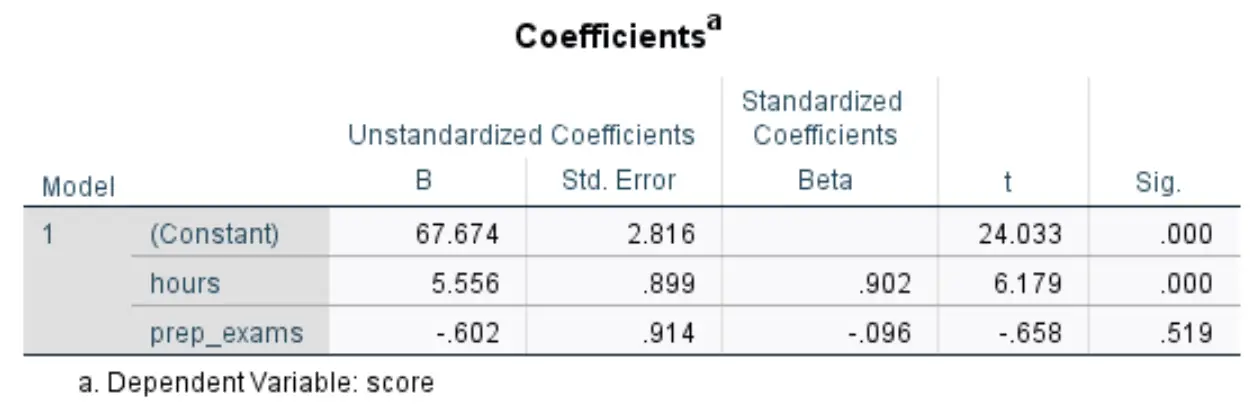
Berikut cara menafsirkan angka paling relevan dalam tabel ini:

• B tidak terstandarisasi (konstan): ini memberitahu kita nilai rata-rata variabel respon ketika kedua variabel prediktor sama dengan nol. Dalam contoh ini, nilai ujian rata-rata adalah 67.674 ketika jam belajar dan ujian persiapan yang diambil sama-sama nol.
• B (jam) yang tidak terstandarisasi: Ini menunjukkan perubahan rata-rata dalam nilai ujian yang terkait dengan peningkatan satu unit jam belajar, dengan asumsi jumlah ujian persiapan yang diambil tetap konstan. Dalam hal ini, setiap tambahan jam yang dihabiskan untuk belajar dikaitkan dengan peningkatan nilai ujian sebesar 5,556 poin, dengan asumsi bahwa jumlah ujian praktik yang diambil tetap konstan.
• B Tidak Terstandar (prep_exams): Ini memberi tahu kita perubahan rata-rata dalam nilai ujian yang terkait dengan peningkatan satu unit dalam ujian persiapan yang diambil, dengan asumsi jumlah jam belajar tetap konstan. Dalam hal ini, setiap ujian persiapan tambahan yang diambil dikaitkan dengan penurunan nilai ujian sebesar 0,602 poin, dengan asumsi jumlah jam belajar tetap konstan.
• tanda tangan. (jam): Ini adalah nilai p untuk variabel penjelas jam . Karena nilai ini (0,000) kurang dari 0,05, kita dapat menyimpulkan bahwa jam belajar memiliki hubungan yang signifikan secara statistik dengan nilai ujian.
• tanda tangan. (prep_exams): Ini adalah nilai p untuk variabel penjelas prep_exams . Karena nilai ini (0,519) tidak kurang dari 0,05, kami tidak dapat menyimpulkan bahwa jumlah ujian persiapan yang diambil mempunyai hubungan yang signifikan secara statistik dengan hasil ujian.

Terakhir, kita dapat membuat persamaan regresi menggunakan nilai yang ditunjukkan pada tabel untuk konstanta , jam , dan prep_exams . Dalam hal ini, persamaannya adalah:

Perkiraan nilai ujian = 67.674 + 5.556*(jam) – 0.602*(ujian_persiapan)

Kita dapat menggunakan persamaan ini untuk mengetahui perkiraan nilai ujian siswa, berdasarkan jumlah jam belajar dan jumlah ujian praktik yang telah mereka ikuti. Misalnya, seorang siswa yang belajar selama 3 jam dan mengikuti 2 ujian persiapan harus menerima nilai ujian 83,1:

Perkiraan nilai ujian = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

Catatan: Karena variabel penjelas untuk persiapan ujian ternyata tidak signifikan secara statistik, kami dapat memutuskan untuk menghapusnya dari model dan melakukan regresi linier sederhana dengan menggunakan jam belajar sebagai satu-satunya variabel penjelas.