Cara melakukan regresi linier sederhana di spss

Regresi linier sederhana merupakan salah satu metode yang dapat kita gunakan untuk memahami hubungan antara variabel prediktor dan variabel respon.

Tutorial ini menjelaskan cara melakukan regresi linier sederhana di SPSS.

Contoh: Regresi Linier Sederhana di SPSS

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan jumlah jam belajar dan nilai ujian yang diperoleh 20 siswa:

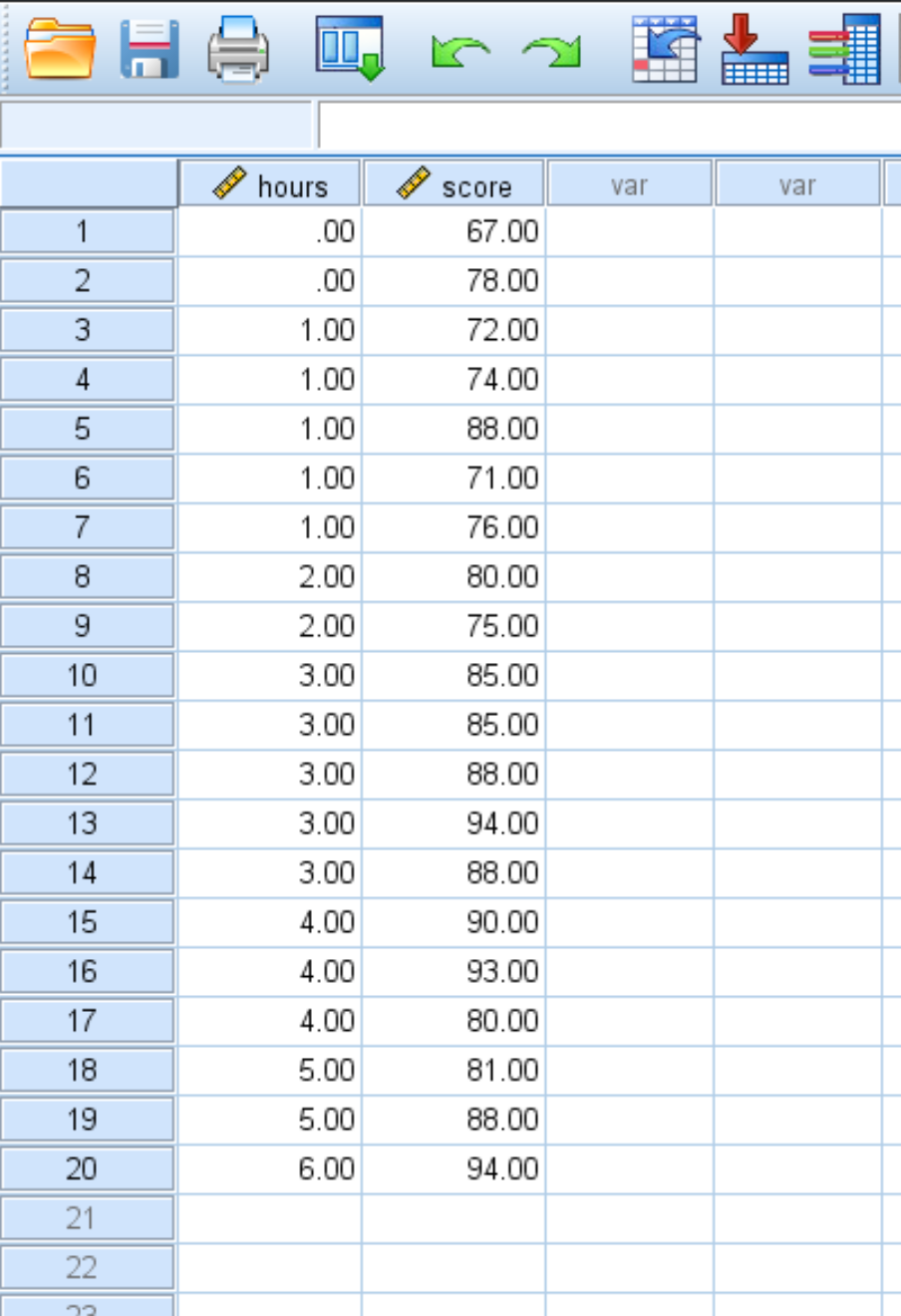
Gunakan langkah-langkah berikut untuk melakukan regresi linier sederhana pada kumpulan data ini untuk mengukur hubungan antara jam belajar dan nilai ujian:

Langkah 1: Visualisasikan datanya.

Pertama, kita akan membuat diagram sebar untuk memvisualisasikan hubungan antara jam dan skor untuk memastikan bahwa hubungan antara kedua variabel tampak linier. Jika tidak, regresi linier sederhana bukanlah teknik yang tepat untuk digunakan.

Klik tab Bagan , lalu klik Pembuat Bagan :

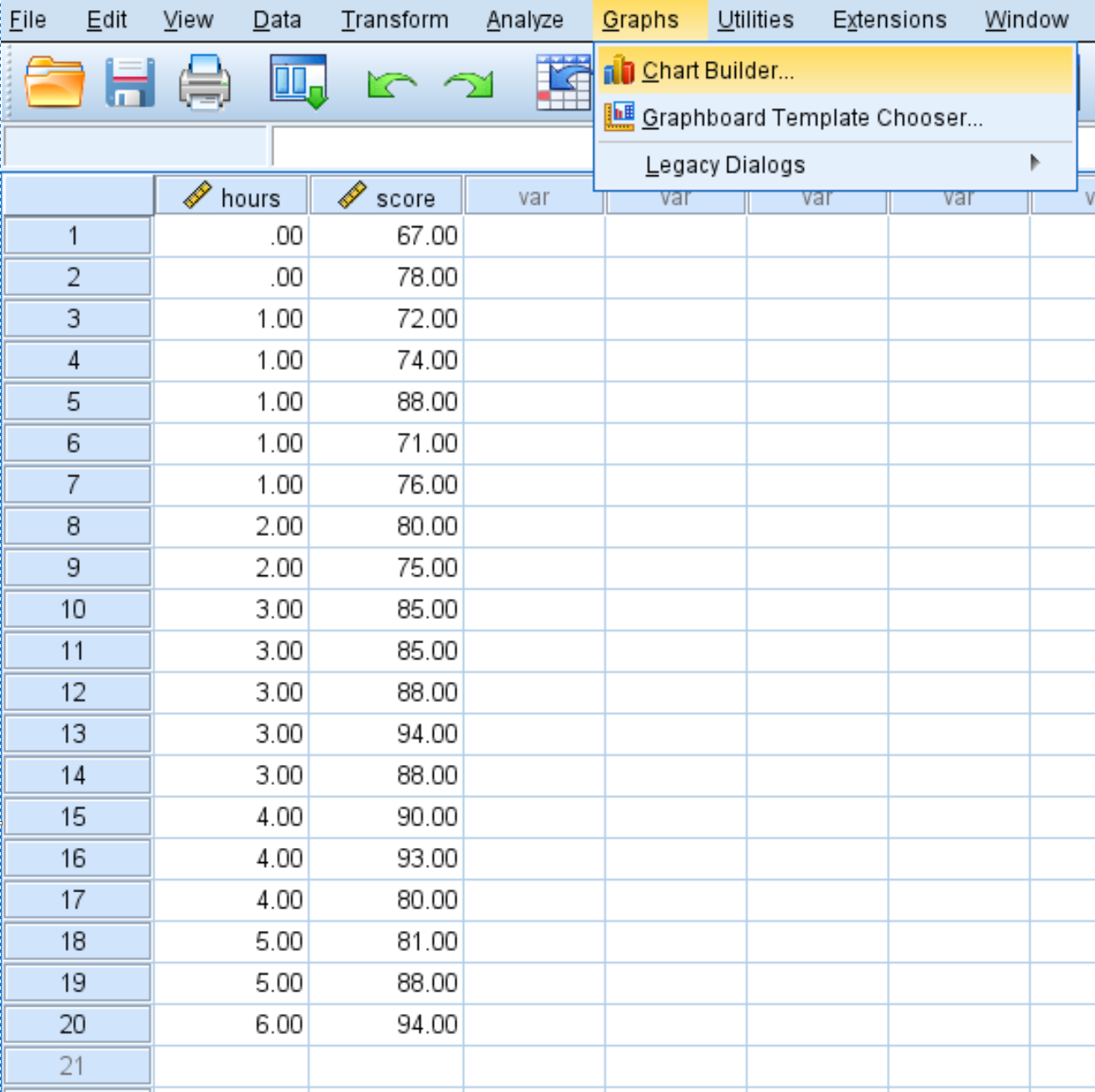
Dari menu Pilih Dari , klik dan seret Sebar/Titik ke dalam jendela pengeditan utama. Kemudian seret variabel waktu ke sumbu x dan skor ke sumbu y.

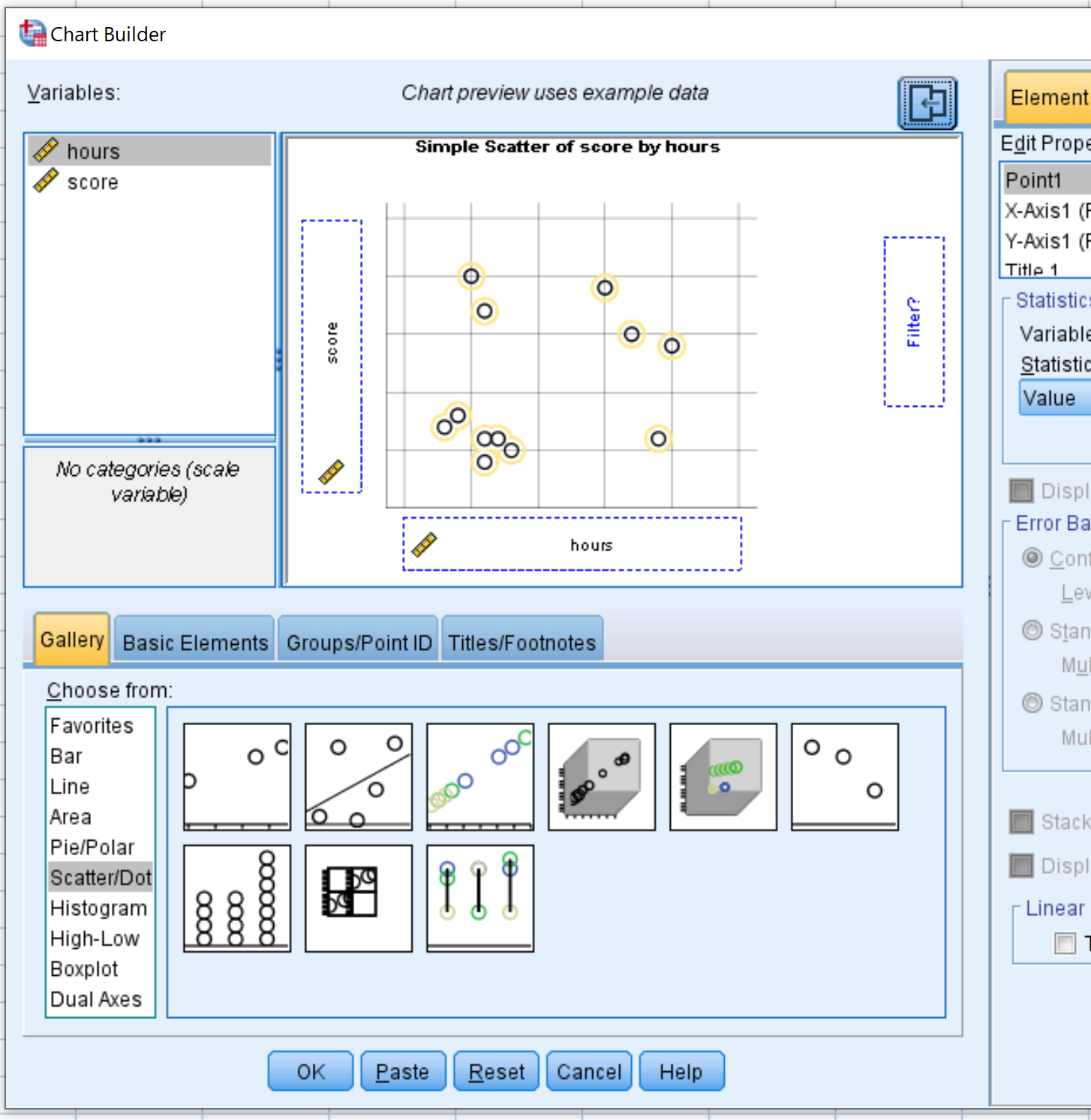
Setelah Anda mengklik OK , plot sebar berikut akan muncul:

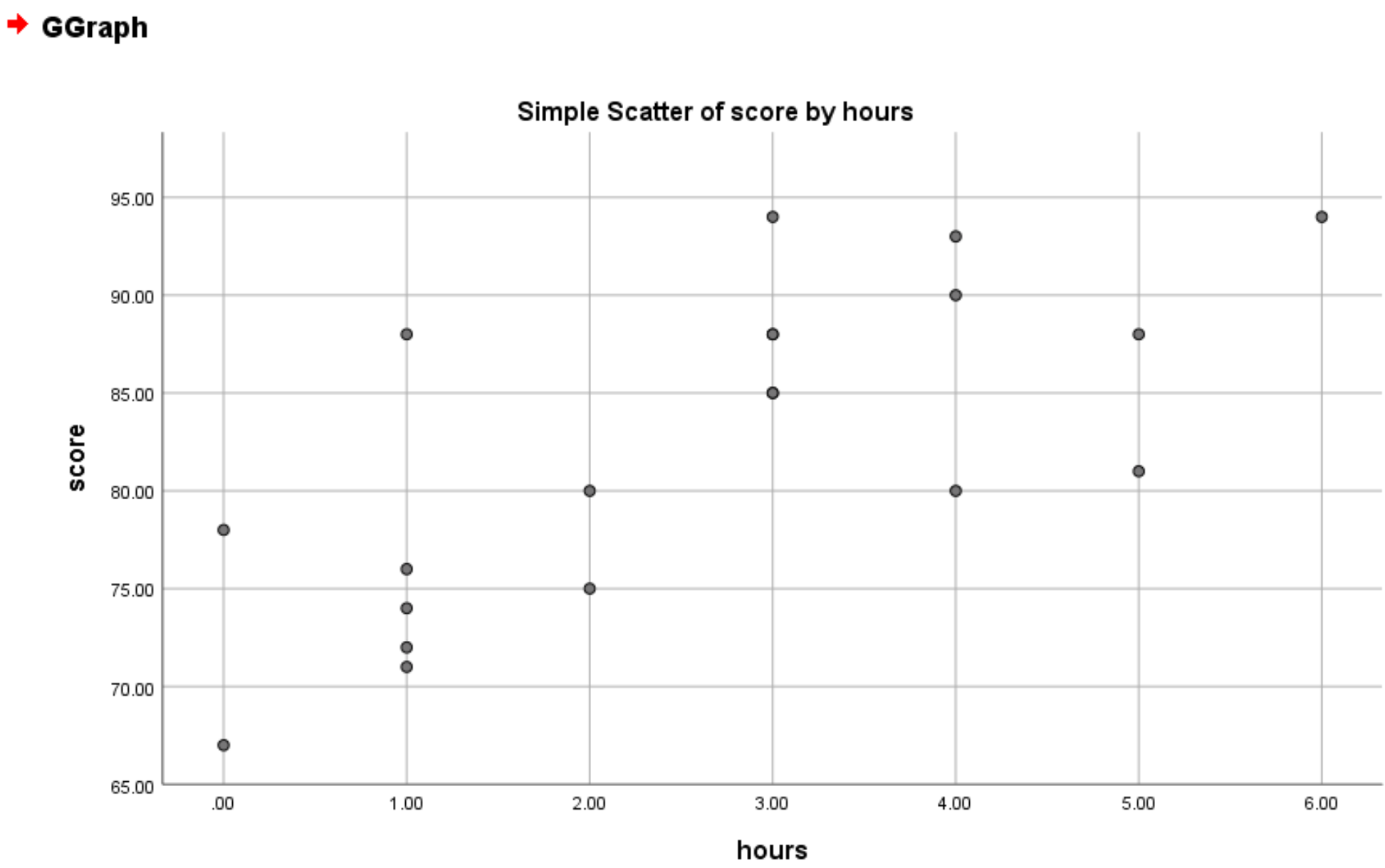
Dari grafik terlihat bahwa terdapat hubungan linier positif antara jam dan skor. Secara umum, siswa yang jam belajarnya lebih lama cenderung mempunyai nilai yang lebih tinggi.

Karena terdapat hubungan linier yang jelas antara kedua variabel, kami akan melanjutkan untuk menyesuaikan model regresi linier sederhana dengan kumpulan data.

Langkah 2: Sesuaikan model regresi linier sederhana.

Klik tab Analisis , lalu Regresi , lalu Linear :

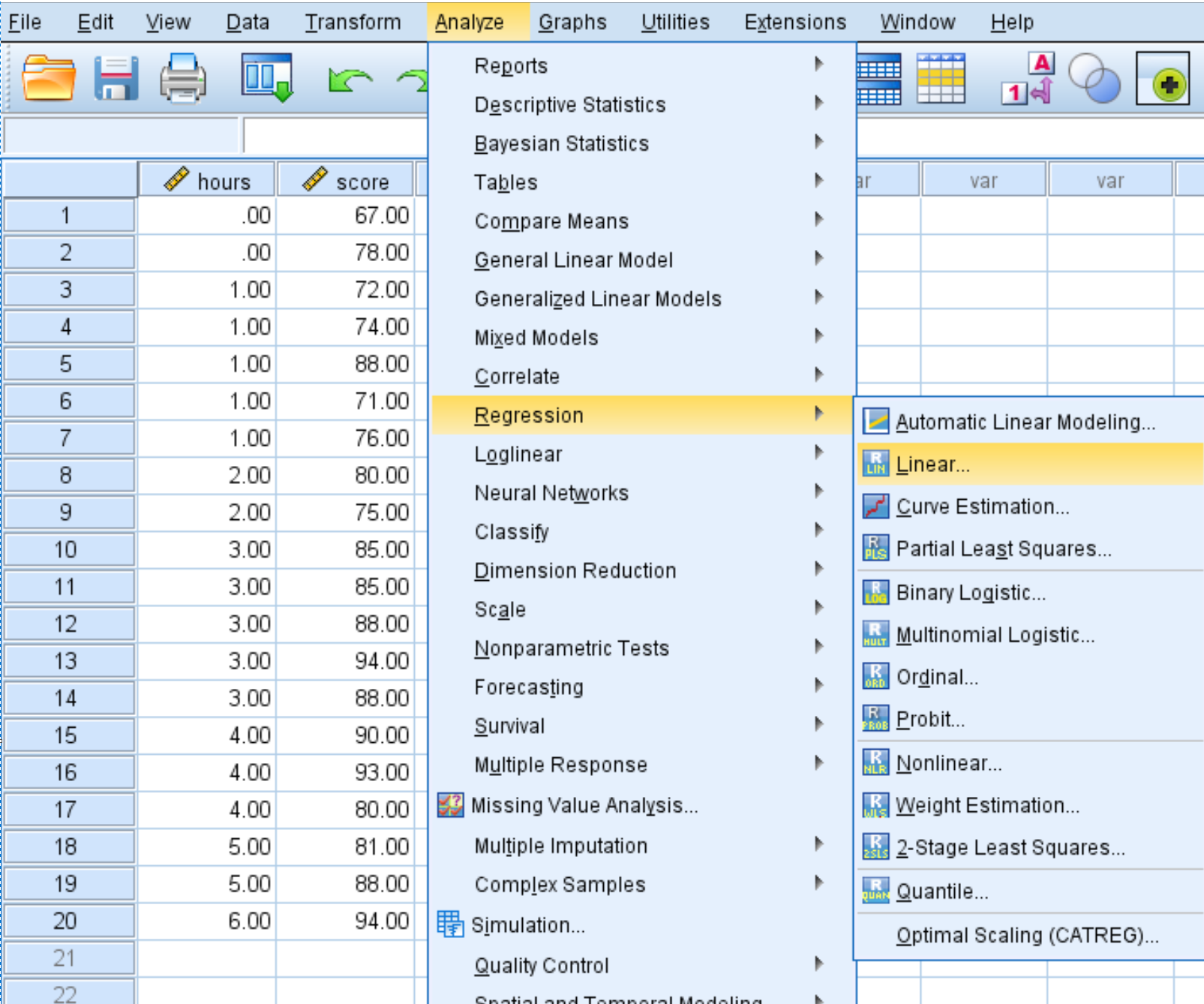
Di jendela baru yang muncul, seret skor variabel ke dalam kotak berlabel Dependent dan seret jam ke dalam kotak berlabel Independen. Lalu klik oke .

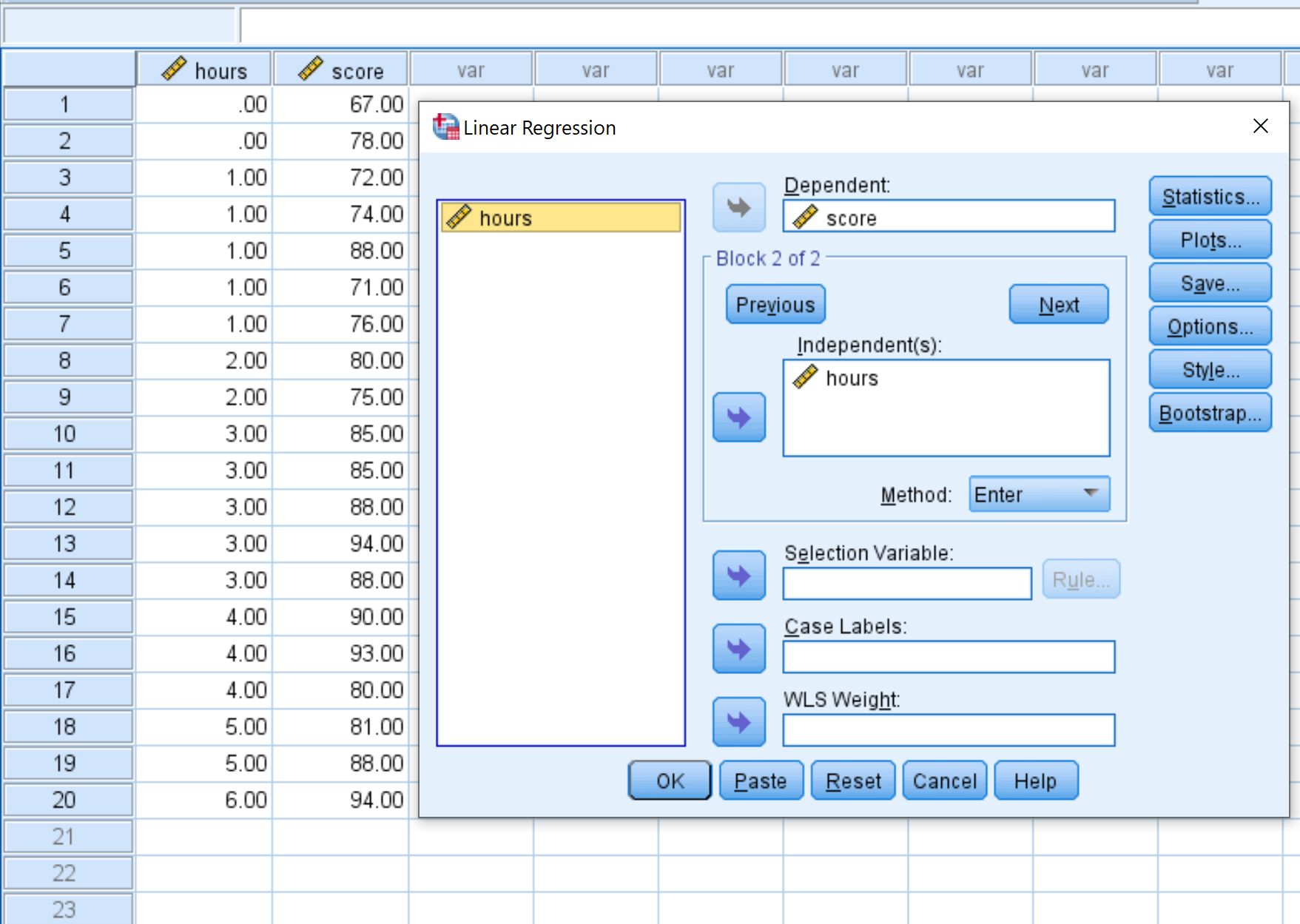
Langkah 3: Interpretasikan hasilnya.

Setelah Anda mengklik OK , akan muncul hasil regresi linier sederhana. Tabel pertama yang menarik minat kami adalah tabel yang berjudul Ringkasan Model :

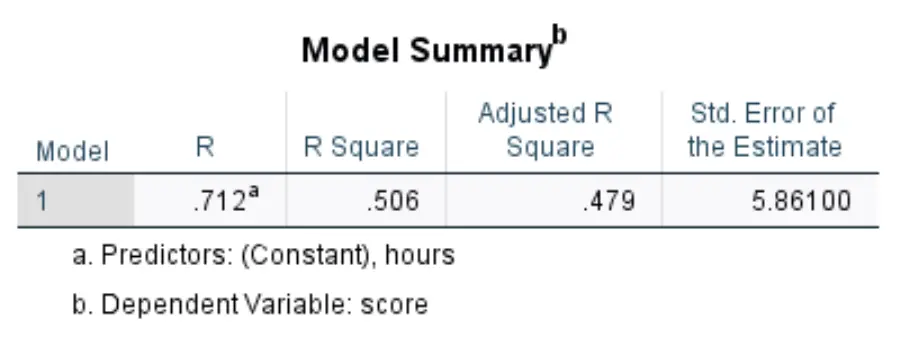
Berikut cara menafsirkan angka paling relevan dalam tabel ini:

• R Square : Merupakan proporsi varians variabel respon yang dapat dijelaskan oleh variabel penjelas. Dalam contoh ini, 50,6% variasi nilai ujian dapat dijelaskan oleh jam belajar.
• Standar. Kesalahan estimasi: kesalahan standar adalah jarak rata-rata antara nilai yang diamati dan garis regresi. Dalam contoh ini, nilai yang diamati rata-rata menyimpang sebesar 5.861 unit dari garis regresi.

Tabel berikut yang menarik minat kami berjudul Koefisien :

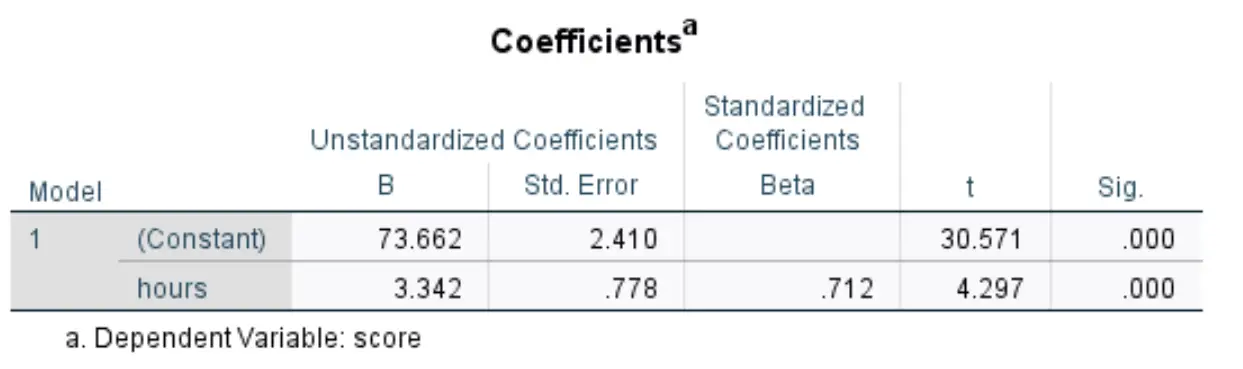
Berikut cara menafsirkan angka paling relevan dalam tabel ini:

• B Tidak Terstandar (Konstan) : Ini memberi tahu kita nilai rata-rata variabel respons ketika variabel prediktornya nol. Dalam contoh ini, rata-rata nilai ujian adalah 73.662 padahal jam belajarnya nol.
• B tidak terstandarisasi (jam): ini memberi tahu kita perubahan rata-rata dalam variabel respons yang terkait dengan peningkatan satu unit dalam variabel prediktor. Dalam contoh ini, setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 3,342 .
• Sig (jam): Ini adalah nilai p yang terkait dengan statistik uji selama jam. Dalam hal ini, karena nilai ini kurang dari 0,05, kita dapat menyimpulkan bahwa variabel prediktor jam kerja signifikan secara statistik.

Terakhir, kita dapat membentuk persamaan regresi menggunakan nilai konstanta dan jam . Dalam hal ini, persamaannya adalah:

Perkiraan nilai ujian = 73.662 + 3.342*(jam)

Kita dapat menggunakan persamaan ini untuk mengetahui perkiraan nilai ujian siswa, berdasarkan jumlah jam belajar.

Misalnya, seorang siswa yang belajar selama 3 jam seharusnya mencapai nilai ujian 83.688:

Estimasi nilai ujian = 73.662 + 3.342*(3) = 83.688

Langkah 4: Laporkan hasilnya.

Terakhir, kami ingin merangkum hasil regresi linier sederhana kami. Berikut ini contoh cara melakukan ini:

Regresi linier sederhana dilakukan untuk mengukur hubungan antara jam belajar dan nilai ujian. Sampel sebanyak 20 siswa digunakan dalam analisis.

Hasilnya menunjukkan bahwa ada hubungan yang signifikan secara statistik antara jam belajar dan nilai ujian (t = 4,297, p <0,000) dan jam belajar menyumbang 50,6% dari variabilitas yang dijelaskan dalam nilai ujian. ujian.

Persamaan regresinya menjadi:

Perkiraan nilai ujian = 73.662 + 3.342*(jam)

Setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata skor ujian sebesar 3,342 .

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SPSS:

Cara melakukan regresi linier berganda di SPSS
Cara melakukan regresi kuadrat di SPSS
Cara melakukan regresi logistik di SPSS