Panduan lembut tentang jumlah kuadrat: sst, ssr, sse
Regresi linier digunakan untuk menemukan garis yang paling “sesuai” dengan sekumpulan data.
Kita sering menggunakan tiga jumlah nilai kuadrat yang berbeda untuk mengukur seberapa cocok garis regresi dengan data:
1. Jumlah Kuadrat Total (SST) – Jumlah kuadrat selisih antara masing-masing titik data ( yi ) dan rata-rata variabel respons ( y ).
- SST = Σ( kamu – kamu ) 2
2. Regresi Jumlah Kuadrat (SSR) – Jumlah kuadrat selisih antara titik data prediksi (ŷ i ) dan rata-rata variabel respons ( y ).
- SSR = Σ(ŷ saya – kamu ) 2
3. Sum of Squares Error (SSE) – Jumlah kuadrat selisih antara titik data prediksi (ŷ i ) dan titik data observasi (y i ).
- SSE = Σ(ŷ saya – y saya ) 2
Terdapat hubungan berikut antara ketiga ukuran ini:
SST = SSR + SSE
Jadi jika kita mengetahui dua pengukuran ini, kita dapat menggunakan aljabar sederhana untuk menghitung pengukuran ketiga.
SSR, SST dan R-Square
R-squared , terkadang disebut koefisien determinasi, adalah ukuran seberapa cocok model regresi linier dengan kumpulan data. Ini mewakili proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor.
Nilai R-squared dapat berkisar antara 0 sampai 1. Nilai 0 menunjukkan bahwa variabel respon tidak dapat dijelaskan sama sekali oleh variabel prediktor. Nilai 1 menunjukkan bahwa variabel respon dapat dijelaskan dengan sempurna tanpa kesalahan oleh variabel prediktor.
Dengan menggunakan SSR dan SST, kita dapat menghitung R kuadrat sebagai berikut:
R kuadrat = SSR / SST
Misalnya, jika SSR untuk model regresi tertentu adalah 137,5 dan SST adalah 156, kita akan menghitung R kuadrat sebagai berikut:
R kuadrat = 137,5 / 156 = 0,8814
Hal ini menunjukkan bahwa 88,14% variasi variabel respon dapat dijelaskan oleh variabel prediktor.
Hitung SST, SSR, SSE: contoh langkah demi langkah
Misalkan kita memiliki kumpulan data berikut yang menunjukkan jumlah jam belajar oleh enam siswa berbeda beserta nilai ujian akhir mereka:
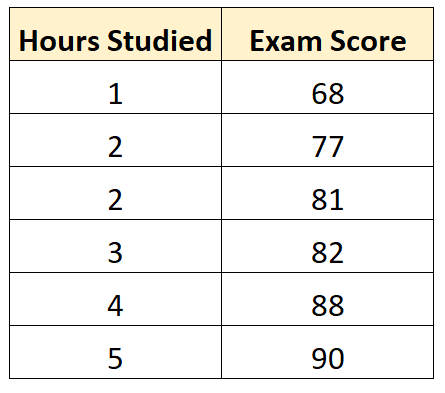
Dengan menggunakan beberapa perangkat lunak statistik (seperti R , Excel , Python ) atau bahkan dengan tangan, kita dapat melihat bahwa garis yang paling sesuai adalah:
Skor = 66.615 + 5.0769*(Jam)
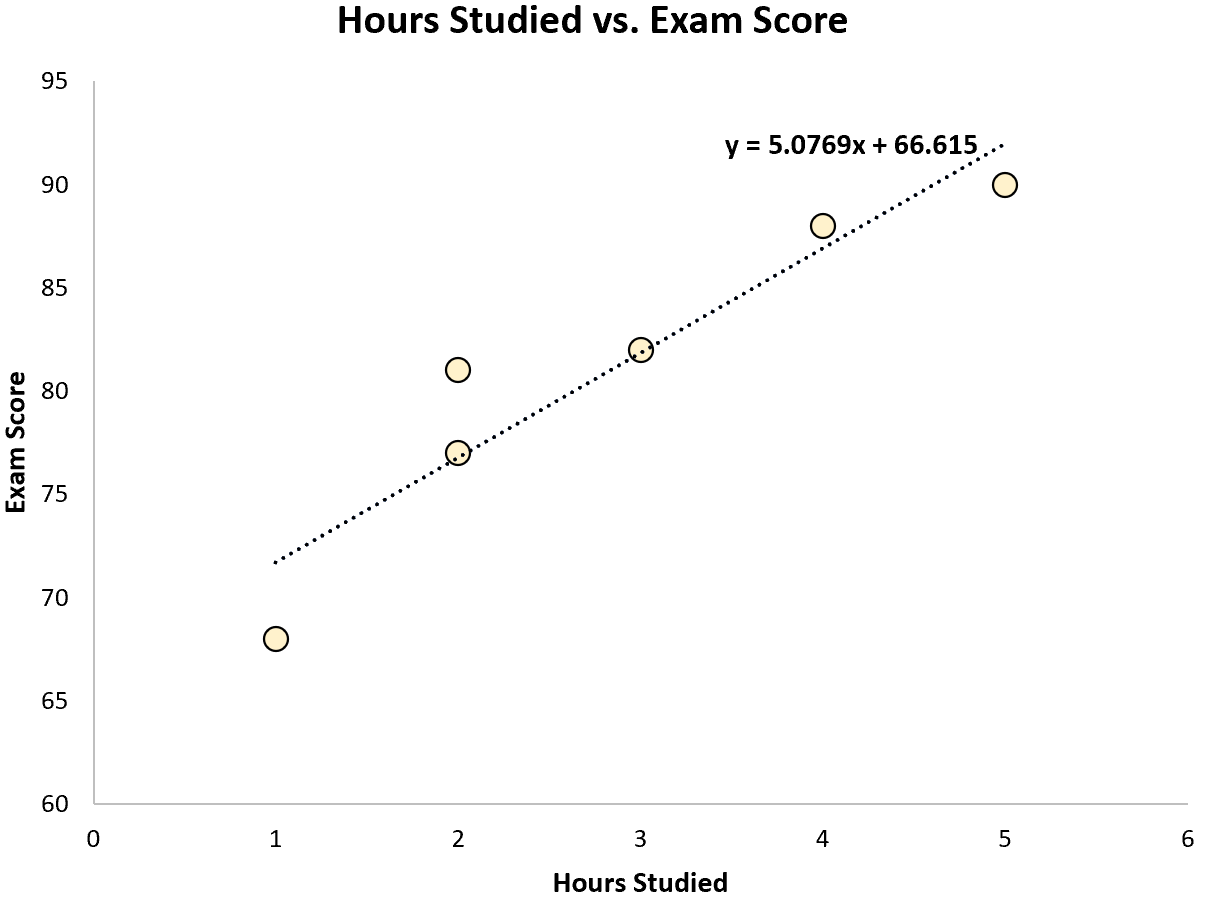
Setelah kita mengetahui garis persamaan yang paling sesuai, kita dapat menggunakan langkah-langkah berikut untuk menghitung SST, SSR, dan SSE:
Langkah 1: Hitung mean dari variabel respon.
Rata-rata variabel respon ( y ) ternyata 81 .
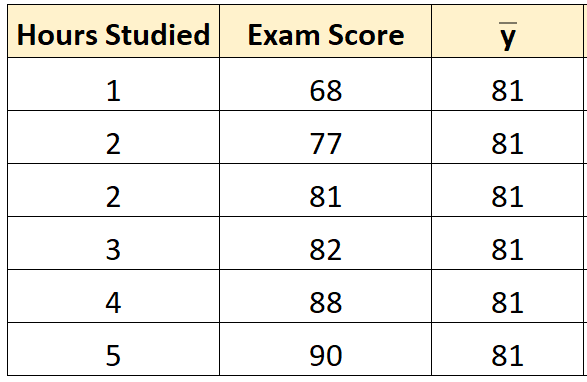
Langkah 2: Hitung nilai prediksi untuk setiap observasi.
Kemudian kita dapat menggunakan garis persamaan yang paling sesuai untuk menghitung prediksi nilai ujian () untuk setiap siswa.
Misalnya prediksi nilai ujian siswa yang belajar satu jam adalah:
Skor = 66.615 + 5.0769*(1) = 71.69 .
Kita dapat menggunakan pendekatan yang sama untuk mencari prediksi skor setiap siswa:
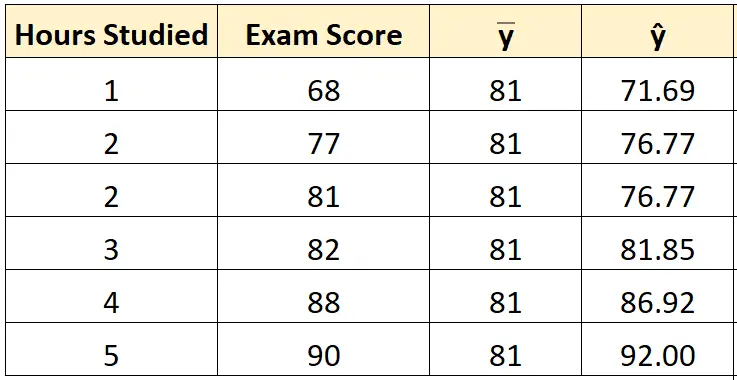
Langkah 3: Hitung jumlah total kuadrat (SST).
Kemudian kita bisa menghitung jumlah total kuadratnya.
Misalnya, jumlah kuadrat siswa pertama adalah:
( kamu – kamu ) 2 = (68 – 81) 2 = 169 .
Kita dapat menggunakan pendekatan yang sama untuk mencari jumlah total kuadrat setiap siswa:
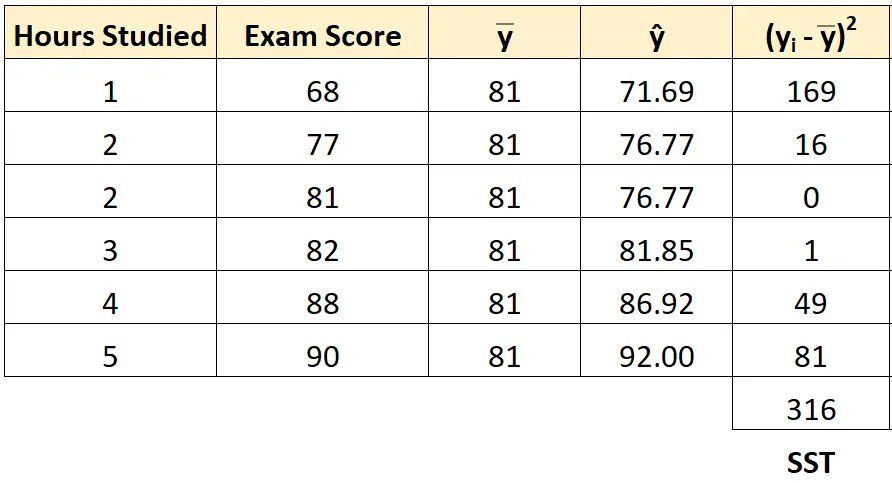
Jumlah total kuadratnya adalah 316 .
Langkah 4: Hitung jumlah regresi kuadrat (SSR).
Kemudian kita bisa menghitung jumlah regresi kuadrat.
Misalnya, jumlah regresi kuadrat untuk siswa pertama adalah:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Kita dapat menggunakan pendekatan yang sama untuk mencari regresi jumlah kuadrat setiap siswa:
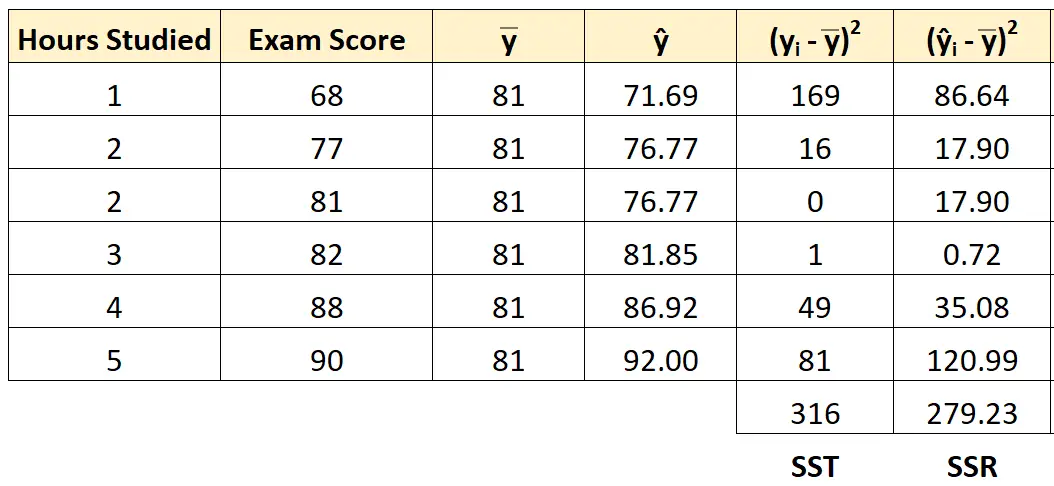
Jumlah regresi kuadrat ternyata 279.23 .
Langkah 5: Hitung jumlah kesalahan kuadrat (SSE).
Kemudian kita bisa menghitung kesalahan jumlah kuadrat.
Misalnya, jumlah kesalahan kuadrat siswa pertama adalah:
(ŷ saya – kamu saya ) 2 = (71,69 – 68) 2 = 13,63 .
Kita dapat menggunakan pendekatan yang sama untuk mencari jumlah kesalahan kuadrat untuk setiap siswa:
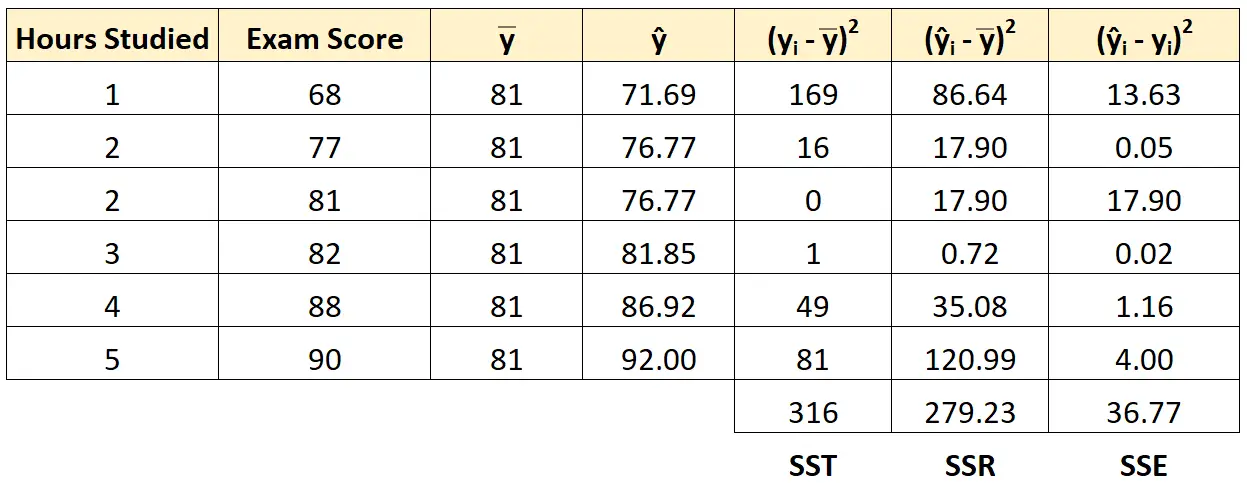
Kami dapat memverifikasi bahwa SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Kita juga dapat menghitung R kuadrat model regresi menggunakan persamaan berikut:
- R kuadrat = SSR / SST
- R kuadrat = 279,23 / 316
- R kuadrat = 0,8836
Hal ini menunjukkan bahwa 88,36% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar.
Sumber daya tambahan
Anda dapat menggunakan kalkulator berikut untuk menghitung SST, SSR, dan SSE secara otomatis untuk garis regresi linier sederhana:
Kalkulator SST
Kalkulator RSS
Kalkulator ESS
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya