Statistik deskriptif atau inferensial: apa bedanya?

Ada dua cabang utama di bidang statistik:

• Statistik deskriptif
• Statistik inferensial

Tutorial ini menjelaskan perbedaan antara kedua cabang dan mengapa masing-masing berguna dalam situasi tertentu.

Statistik deskriptif

Singkatnya, statistik deskriptif bertujuan untuk mendeskripsikan sekumpulan data mentah menggunakan ringkasan statistik, grafik, dan tabel.

Statistik deskriptif berguna karena memungkinkan Anda memahami sekelompok data dengan lebih cepat dan mudah dibandingkan hanya melihat baris demi baris nilai data mentah.

Misalnya, kita memiliki kumpulan data mentah yang menunjukkan nilai ujian 1.000 siswa di sekolah tertentu. Kami mungkin tertarik pada nilai tes rata-rata serta distribusi nilai tes.

Dengan menggunakan statistik deskriptif, kita dapat menemukan skor rata-rata dan membuat grafik yang membantu kita memvisualisasikan distribusi skor.

Hal ini memungkinkan kami untuk memahami nilai ujian siswa dengan lebih mudah dibandingkan hanya melihat data mentah.

Bentuk umum statistik deskriptif

Ada tiga bentuk umum statistik deskriptif:

1. Ringkasan statistik. Ini adalah statistik yang merangkum data menggunakan satu angka. Ada dua jenis statistik ringkasan yang umum:

• Ukuran tendensi sentral : Angka-angka ini menjelaskan letak pusat suatu kumpulan data. Contohnya termasuk rata-rata   dan mediannya .
• Ukuran penyebaran: Angka-angka ini menggambarkan distribusi nilai dalam kumpulan data. Contohnya termasuk interval , rentang antarkuartil , deviasi standar, dan varians .

2. Grafik . Bagan membantu kita memvisualisasikan data. Jenis bagan umum yang digunakan untuk memvisualisasikan data mencakup plot kotak , histogram , plot batang dan daun, sertaplot sebar .

3. Tabel . Tabel dapat membantu kita memahami bagaimana data didistribusikan. Jenis tabel yang umum adalah tabel frekuensi , yang memberi tahu kita berapa banyak nilai data yang berada dalam rentang tertentu.

Contoh penggunaan statistik deskriptif

Contoh berikut mengilustrasikan bagaimana kita dapat menggunakan statistik deskriptif di dunia nyata.

Diasumsikan 1.000 siswa di sekolah tertentu semuanya mengikuti tes yang sama. Kami ingin memahami distribusi hasil tes, jadi kami menggunakan statistik deskriptif berikut:

1. Ringkasan statistik

Rata-rata: 82,13 . Hal ini menunjukkan bahwa rata-rata nilai tes di antara 1.000 siswa adalah 82,13.

Median: 84. Hal ini menunjukkan bahwa separuh siswa mendapat nilai di atas 84 dan separuh lainnya mendapat nilai di bawah 84.

Maks: 100. Min: 45. Artinya, skor maksimum yang diperoleh setiap siswa adalah 100 dan skor minimum adalah 45. Kisaran – yang menunjukkan perbedaan antara maksimum dan minimum – adalah 55.

2. Grafik

Untuk memvisualisasikan distribusi hasil pengujian, kita dapat membuat histogram – sejenis grafik yang menggunakan batang persegi panjang untuk mewakili frekuensi.

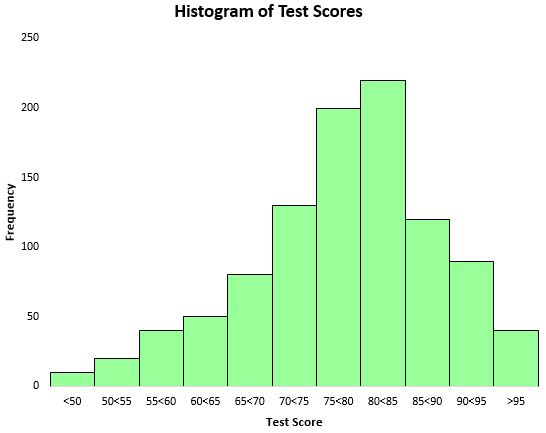
Berdasarkan histogram ini, kita dapat melihat bahwa sebaran nilai tes secara kasar berbentuk lonceng. Sebagian besar siswa mendapat nilai antara 70 dan 90, sementara sangat sedikit siswa yang mendapat nilai di atas 95 dan bahkan lebih sedikit lagi yang mendapat nilai di bawah 50.

3. Tabel

Cara mudah lainnya untuk memahami distribusi skor adalah dengan membuat tabel frekuensi. Misalnya, tabel frekuensi berikut menunjukkan persentase siswa yang mendapat nilai di antara rentang yang berbeda:

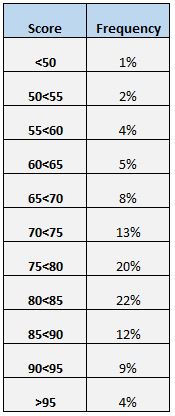
Kita dapat melihat bahwa hanya 4% dari total siswa yang mendapat nilai di atas 95. Kita juga dapat melihat bahwa (12% + 9% + 4% = ) 25% dari seluruh siswa mendapat nilai 85 atau lebih.

Tabel frekuensi sangat berguna jika kita ingin mengetahui berapa persentase nilai data yang berada di atas atau di bawah nilai tertentu. Misalnya, sekolah menganggap nilai ujian yang “dapat diterima” adalah nilai di atas 75.

Melihat tabel frekuensi, kita dapat dengan mudah melihat bahwa (20% + 22% + 12% + 9% + 4% = ) 67% siswa menerima nilai ujian yang dapat diterima.

Statistik inferensial

Singkatnya, statistik inferensial menggunakan sampel data yang kecil untuk menarik kesimpulan tentang populasi yang lebih besar dari mana sampel tersebut diambil.

Misalnya, kita mungkin ingin memahami preferensi politik jutaan orang di suatu negara.

Namun, akan memakan waktu dan biaya yang terlalu besar untuk mensurvei setiap individu di suatu negara. Jadi, kita akan melakukan survei yang lebih kecil, katakanlah, terhadap 1.000 orang Amerika, dan menggunakan hasil survei tersebut untuk menarik kesimpulan tentang populasi secara keseluruhan.

Inilah keseluruhan premis statistik inferensial: kita ingin menjawab pertanyaan tentang suatu populasi, jadi kita memperoleh data untuk sampel kecil dari populasi tersebut dan menggunakan data sampel tersebut untuk menarik kesimpulan tentang populasi tersebut.

Pentingnya sampel yang representatif

Agar yakin dengan kemampuan kita menggunakan sampel untuk menarik kesimpulan tentang suatu populasi, kita harus memastikan bahwa kita memiliki sampel yang representatif , yaitu sampel yang karakteristik individu dalam populasi Sampel tersebut sangat cocok dengan sampelnya. karakteristik. dari keseluruhan populasi.

Idealnya, kita ingin sampel kita menyerupai “versi mini” dari populasi kita. Jadi, jika kita ingin menarik kesimpulan tentang populasi siswa yang terdiri dari 50% perempuan dan 50% laki-laki, sampel kita tidak akan representatif jika mencakup 90% laki-laki dan hanya 10% perempuan.

Jika sampel kita tidak sama dengan populasi secara keseluruhan, kita tidak dapat dengan yakin menggeneralisasikan hasil dari sampel ke populasi secara keseluruhan.

Cara mendapatkan sampel yang representatif

Untuk memaksimalkan peluang memperoleh sampel yang representatif, Anda harus fokus pada dua hal:

1. Pastikan Anda menggunakan metode pengambilan sampel secara acak.

Ada beberapa metode pengambilan sampel acak yang dapat Anda gunakan yang kemungkinan besar akan menghasilkan sampel yang representatif, antara lain:

• Sampel acak sederhana
• Sampel acak yang sistematis
• Sampel acak cluster
• Sampel acak bertingkat

Metode pengambilan sampel secara acak cenderung menghasilkan sampel yang representatif karena setiap anggota populasi mempunyai peluang yang sama untuk dijadikan sampel.

2. Pastikan ukuran sampel Anda cukup besar .

Selain menggunakan metode pengambilan sampel yang tepat, penting untuk memastikan bahwa sampelnya cukup besar sehingga Anda memiliki cukup data untuk dapat melakukan generalisasi ke populasi yang lebih besar.

Untuk menentukan ukuran sampel, Anda perlu mempertimbangkan ukuran populasi yang Anda pelajari, tingkat kepercayaan yang ingin Anda gunakan, dan margin kesalahan yang Anda anggap dapat diterima.

Untungnya, Anda dapat menggunakan kalkulator online untuk memasukkan nilai-nilai ini dan melihat berapa ukuran sampel Anda.

Bentuk umum statistik inferensial

Ada tiga bentuk umum statistik inferensial:

1. Pengujian hipotesis.

Kami sering ingin menjawab pertanyaan tentang populasi seperti:

• Apakah persentase masyarakat di Ohio yang mendukung Kandidat A lebih dari 50%?
• Apakah tinggi rata-rata tanaman tertentu sama dengan 14 inci?
• Apakah ada perbedaan rata-rata tinggi badan siswa di sekolah A dan sekolah B?

Untuk menjawab pertanyaan-pertanyaan ini, kita dapat melakukan pengujian hipotesis , yang memungkinkan kita menggunakan data dari sampel untuk menarik kesimpulan tentang populasi.

2. Interval kepercayaan .

Terkadang kita ingin memperkirakan nilai tertentu untuk suatu populasi. Misalnya, kita mungkin tertarik pada tinggi rata-rata spesies tumbuhan tertentu di Australia.

Daripada berkeliling dan mengukur setiap tanaman di suatu negara, kita bisa mengumpulkan sampel kecil tanaman dan mengukur masing-masing tanaman. Kemudian kita dapat menggunakan rata-rata tinggi tanaman dalam sampel untuk memperkirakan rata-rata tinggi populasi.

Namun, sampel kami tidak mungkin memberikan estimasi populasi yang sempurna. Untungnya, kita dapat menjelaskan ketidakpastian ini dengan membuat interval kepercayaan , yang memberikan rentang nilai yang di dalamnya kita yakin bahwa parameter populasi sebenarnya berada.

Misalnya, kita dapat menghasilkan interval kepercayaan 95% sebesar [13,2, 14,8], yang berarti kita yakin 95% bahwa rata-rata tinggi sebenarnya spesies tanaman ini adalah antara 13,2 inci dan 14,8 inci.

3. Regresi .

Terkadang kita ingin memahami hubungan antara dua variabel dalam suatu populasi.

Misalnya, kita ingin mengetahui apakah jumlah jam yang dihabiskan untuk belajar per minggu berhubungan dengan nilai ujian . Untuk menjawab pertanyaan ini, kita dapat melakukan teknik yang disebut analisis regresi .

Jadi, kita dapat melihat jumlah jam belajar serta nilai ujian untuk 100 siswa dan melakukan analisis regresi untuk melihat apakah terdapat hubungan yang signifikan antara kedua variabel tersebut.

Jika p-value regresi terbukti signifikan , maka dapat disimpulkan bahwa terdapat hubungan yang signifikan antara kedua variabel tersebut pada populasi siswa secara keseluruhan.

Perbedaan antara statistik deskriptif dan inferensial

Secara ringkas perbedaan statistik deskriptif dan inferensial dapat diuraikan sebagai berikut:

Statistik deskriptif menggunakan statistik ringkasan, grafik, dan tabel untuk menggambarkan sekumpulan data.

Hal ini berguna untuk membantu kita memahami sekumpulan data dengan cepat dan mudah tanpa melalui semua nilai data individual.

Statistik inferensial menggunakan sampel untuk menarik kesimpulan tentang populasi yang lebih besar.

Bergantung pada pertanyaan yang ingin Anda jawab tentang suatu populasi, Anda dapat memutuskan untuk menggunakan satu atau lebih metode berikut: pengujian hipotesis, interval kepercayaan, dan analisis regresi.

Jika Anda memilih untuk menggunakan salah satu metode ini, ingatlah bahwa sampel Anda harus mewakili populasi Anda , jika tidak, kesimpulan yang Anda ambil tidak akan dapat diandalkan.