Cara menguji normalitas di stata

Banyak uji statistik yang mengharuskan satu atau lebih variabel berdistribusi normal agar hasil pengujian dapat diandalkan.

Tutorial ini menjelaskan beberapa metode yang dapat Anda gunakan untuk menguji normalitas antar variabel di Stata.

Untuk masing-masing metode ini, kita akan menggunakan kumpulan data Stata bawaan yang disebut auto . Anda dapat memuat kumpulan data ini menggunakan perintah berikut:

penggunaan otomatis sistem

Metode 1: histogram

Cara informal untuk melihat apakah suatu variabel terdistribusi normal adalah dengan membuat histogram untuk menampilkan distribusi variabel.

Jika variabel terdistribusi normal, histogram akan berbentuk “lonceng” dengan lebih banyak nilai terletak di dekat pusat dan lebih sedikit nilai terletak di bagian ekor.

Kita dapat menggunakan perintah hist untuk membuat histogram untuk variabel perpindahan :

sejarah yang bergerak

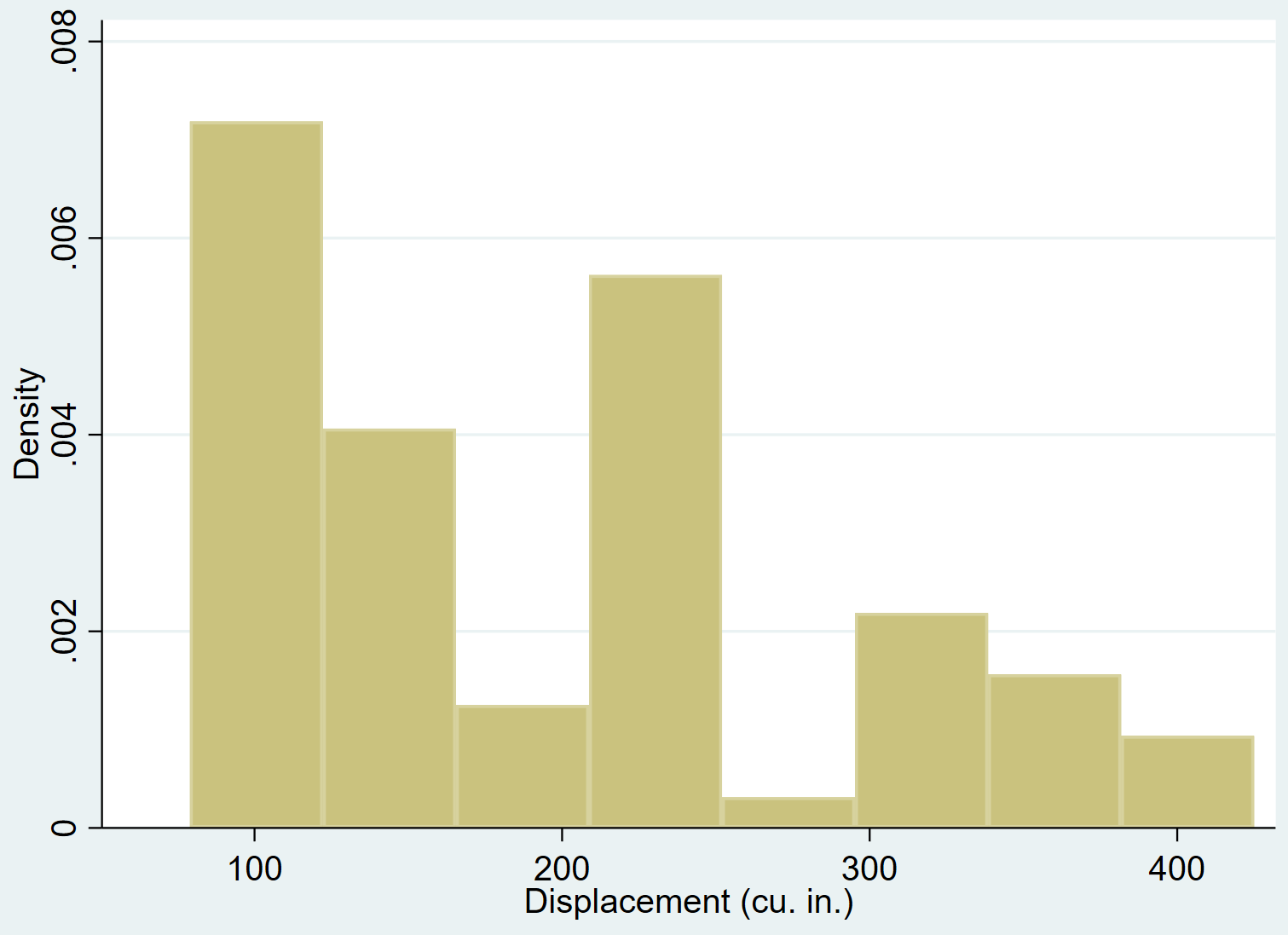
Kita dapat menambahkan kurva kepadatan normal ke histogram menggunakan perintah normal :

sejarah bergerak, normal

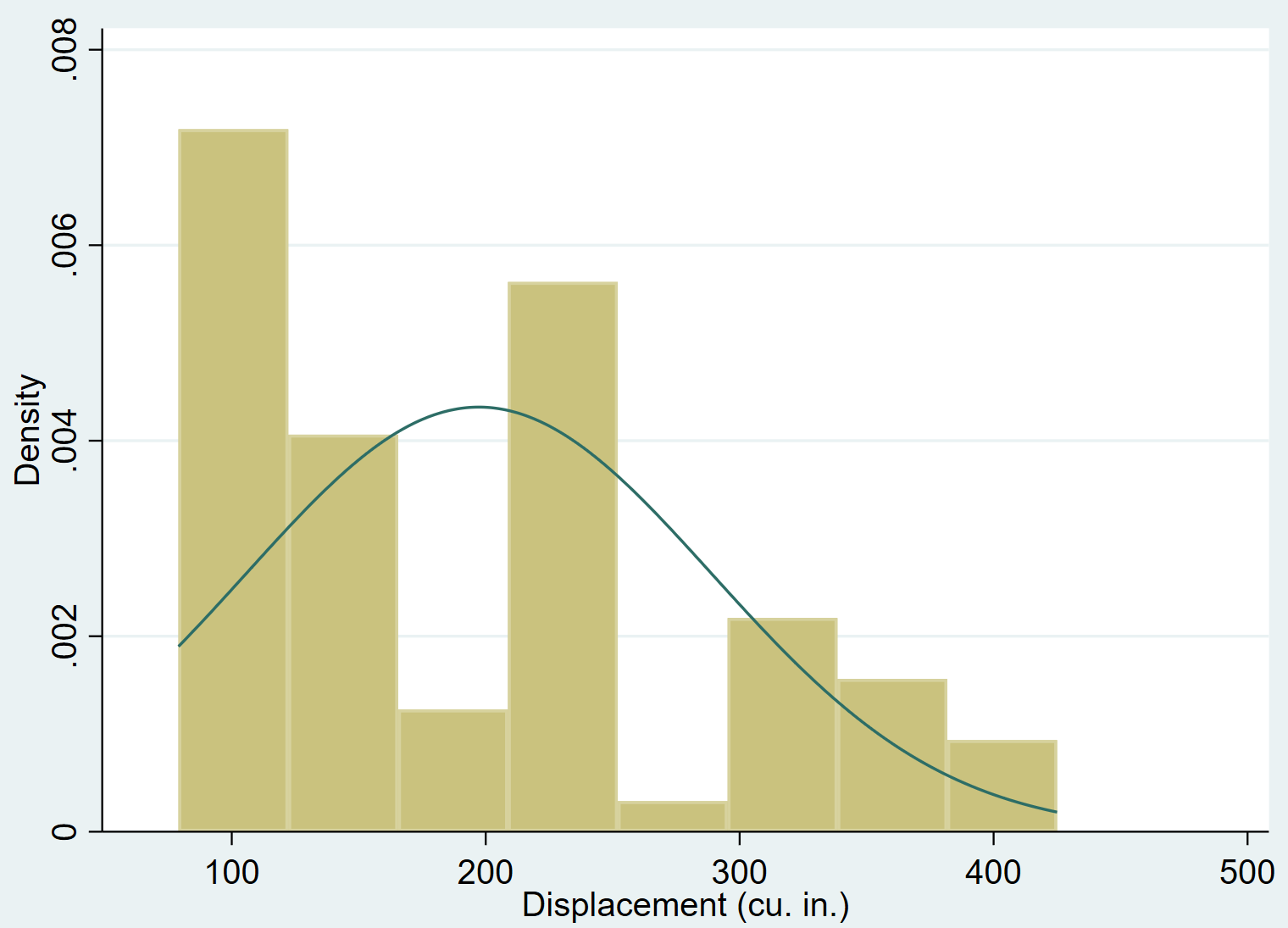
Sangat jelas terlihat bahwa pergeseran variabel condong ke kanan (misalnya sebagian besar nilai terkonsentrasi di kiri dan “ekor” nilai yang panjang memanjang ke kanan) dan tidak mengikuti distribusi normal.

Terkait: Distribusi Miring Kiri dan Kanan

Metode 2: Tes Shapiro-Wilk

Cara formal untuk menguji normalitas adalah dengan menggunakan uji Shapiro-Wilk .

Hipotesis nol untuk pengujian ini adalah variabel terdistribusi normal. Jika nilai p pengujian berada di bawah tingkat signifikansi tertentu (pilihan umum mencakup 0,01, 0,05, dan 0,10), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat cukup bukti untuk menyatakan bahwa variabel tersebut tidak terdistribusi normal. .

*Tes ini dapat digunakan ketika jumlah observasi antara 4 dan 2.000.

Kita dapat menggunakan perintah swilk untuk melakukan tes Shapiro-Wilk pada variabel perpindahan :

gerakan halus

Berikut cara menafsirkan hasil tes:

Obs: 74. Ini adalah jumlah observasi yang digunakan dalam tes.

W: 0,92542. Ini adalah statistik pengujian untuk pengujian tersebut.

Masalah>z: 0,00031. Ini adalah nilai p yang terkait dengan statistik uji.

Karena nilai p kurang dari 0,05, kita dapat menolak hipotesis nol dari pengujian tersebut. Kami mempunyai cukup bukti untuk mengatakan bahwa perpindahan variabel tidak terdistribusi normal.

Kita juga dapat melakukan uji Shapiro-Wilk pada beberapa variabel sekaligus dengan mencantumkan beberapa variabel setelah perintah swilk :

perpindahan swilk panjang mpg

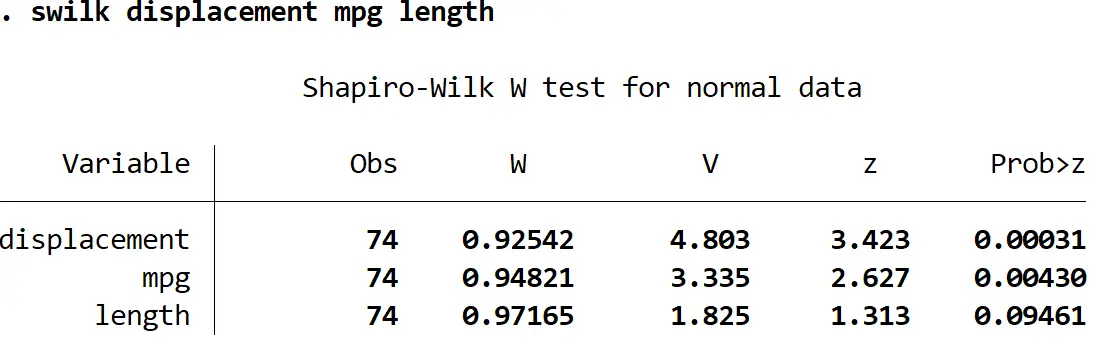
Dengan menggunakan tingkat signifikansi 0,05, kita dapat menyimpulkan bahwa perpindahan dan mpg tidak terdistribusi secara normal, namun kita tidak memiliki cukup bukti untuk mengatakan bahwa panjang tidak terdistribusi secara normal.

Metode 3: Tes Shapiro-Francia

Cara formal lain untuk menguji normalitas adalah dengan menggunakan uji Shapiro-Francia .

Hipotesis nol untuk pengujian ini adalah variabel terdistribusi normal. Jika nilai p pengujian berada di bawah tingkat signifikansi tertentu, maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat cukup bukti untuk mengatakan bahwa variabel tersebut tidak terdistribusi normal.

*Tes ini dapat digunakan ketika jumlah observasi antara 10 dan 5.000.

Kita dapat menggunakan perintah sfrancia untuk melakukan Tes Shapiro-Wilk pada perpindahan variabel :

memindahkan sfrancia

Berikut cara menafsirkan hasil tes:

Obs: 74. Ini adalah jumlah observasi yang digunakan dalam tes.

W’: 0,93011. Ini adalah statistik pengujian untuk pengujian tersebut.

Masalah>z: 0,00094. Ini adalah nilai p yang terkait dengan statistik uji.

Karena nilai p kurang dari 0,05, kita dapat menolak hipotesis nol dari pengujian tersebut. Kami mempunyai cukup bukti untuk mengatakan bahwa perpindahan variabel tidak terdistribusi normal.

Mirip dengan pengujian Shapiro-Wilk, Anda dapat melakukan pengujian Shapiro-Francia pada beberapa variabel sekaligus dengan mencantumkan beberapa variabel setelah perintah sfrancia .

Metode 4: pengujian kemiringan dan kurtosis

Cara lain untuk menguji normalitas adalah dengan menggunakan uji skewness dan kurtosis , yang menentukan apakah skewness dan kurtosis suatu variabel sesuai dengan distribusi normal atau tidak.

Hipotesis nol untuk pengujian ini adalah variabel terdistribusi normal. Jika nilai p pengujian berada di bawah tingkat signifikansi tertentu, maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat cukup bukti untuk mengatakan bahwa variabel tersebut tidak terdistribusi normal.

*Tes ini memerlukan minimal 8 observasi untuk dapat digunakan.

Kita dapat menggunakan perintah sktest untuk melakukan uji skewness dan kurtosis pada variabel perpindahan :

memindahkan tes

Berikut cara menafsirkan hasil tes:

Obs: 74. Ini adalah jumlah observasi yang digunakan dalam tes.

adj chi(2): 5.81. Ini adalah statistik uji chi-kuadrat untuk pengujian tersebut.

Masalah>chi2: 0,0547. Ini adalah nilai p yang terkait dengan statistik uji.

Karena nilai p tidak kurang dari 0,05, kami gagal menolak hipotesis nol dari pengujian tersebut. Kami tidak memiliki cukup bukti untuk mengatakan bahwa pergerakan tidak terdistribusi secara normal.

Mirip dengan uji normalitas lainnya, Anda dapat melakukan uji skewness dan kurtosis pada beberapa variabel sekaligus dengan mencantumkan beberapa variabel setelah perintah sktest .