Apa yang dimaksud dengan statistik uji standar?
Hipotesis statistik adalah asumsi tentang parameter populasi . Misalnya, kita dapat berasumsi bahwa rata-rata tinggi badan pria di Amerika Serikat adalah 70 inci. Hipotesis mengenai tinggi badan adalah hipotesis statistik dan rata-rata tinggi badan sebenarnya seorang pria di Amerika Serikat adalah parameter populasi .
Uji hipotesis adalah uji statistik formal yang kita gunakan untuk menolak atau gagal menolak hipotesis statistik.
Proses dasar untuk melakukan pengujian hipotesis adalah sebagai berikut:
1. Kumpulkan data sampel.
2. Hitung statistik uji standar untuk data sampel.
3. Bandingkan statistik uji standar dengan nilai kritis. Jika lebih ekstrim dari nilai kritisnya, tolak hipotesis nol. Jika tidak, jangan menolak uji hipotesis nol.
Rumus yang kami gunakan untuk menghitung statistik uji standar bervariasi tergantung pada jenis pengujian hipotesis yang kami lakukan.
Tabel berikut menunjukkan rumus yang digunakan untuk menghitung statistik uji standar untuk masing-masing dari empat jenis utama pengujian hipotesis:
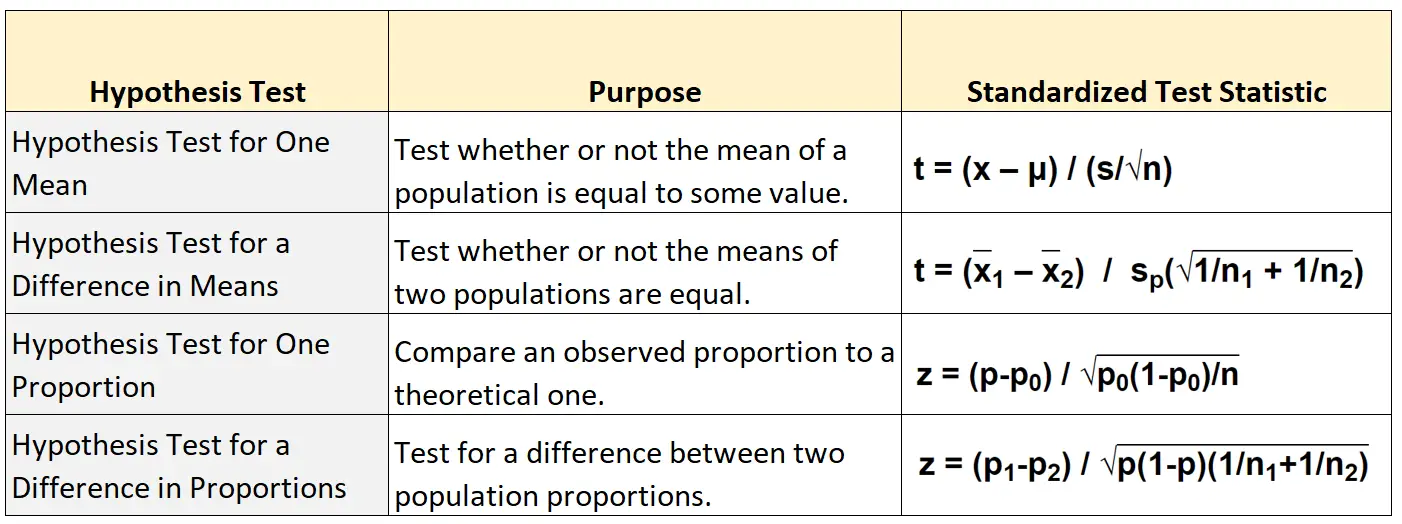
Pengujian hipotesis untuk rata-rata
Uji-t satu sampel digunakan untuk menguji apakah rata-rata suatu populasi sama dengan nilai tertentu atau tidak.
Statistik tes standar untuk jenis tes ini dihitung sebagai berikut:
t = ( X – μ) / (s/√n)
Emas:
- x: sarana sampel
- μ 0 : rata-rata populasi hipotetis
- s: deviasi standar sampel
- n: ukuran sampel
Lihat tutorial ini untuk contoh penghitungan statistik pengujian standar ini.
Pengujian hipotesis untuk perbedaan rata-rata
Uji-t dua sampel digunakan untuk menguji apakah rata-rata dua populasi sama atau tidak.
Statistik tes standar untuk jenis tes ini dihitung sebagai berikut:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
dimana x 1 dan x 2 adalah mean sampel, n 1 dan n 2 adalah ukuran sampel, dan dimana s p dihitung sebagai berikut:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
dimana s 1 2 dan s 2 2 adalah varians sampel.
Lihat tutorial ini untuk contoh penghitungan statistik pengujian standar ini.
Pengujian hipotesis untuk suatu proporsi
Uji z satu proporsi digunakan untuk membandingkan proporsi yang diamati dengan proporsi teoritis.
Statistik tes standar untuk jenis tes ini dihitung sebagai berikut:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
Emas:
- p: proporsi sampel yang diamati
- p 0 : proporsi hipotetis populasi
- n: ukuran sampel
Lihat tutorial ini untuk contoh penghitungan statistik pengujian standar ini.
Pengujian hipotesis untuk perbedaan proporsi
Uji z dua proporsi digunakan untuk menguji perbedaan antara dua proporsi populasi.
Statistik tes standar untuk jenis tes ini dihitung sebagai berikut:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
dimana p 1 dan p 2 adalah proporsi sampel, n 1 dan n 2 adalah ukuran sampel, dan dimana p adalah total proporsi gabungan yang dihitung sebagai berikut:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Lihat tutorial ini untuk contoh penghitungan statistik pengujian standar ini.
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya