Teorema bayes

Oleh Benjamin anderson Agustus 1, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu teorema Bayes dan kegunaannya dalam probabilitas dan statistik. Dengan demikian, Anda akan menemukan apa rumus teorema Bayes, contoh penyelesaian teorema Bayes, dan apa saja penerapan teorema tersebut.

Apa teorema Bayes?

Dalam teori probabilitas, teorema Bayes adalah hukum yang digunakan untuk menghitung probabilitas suatu peristiwa ketika informasi apriori tentang peristiwa tersebut diketahui.

Lebih khusus lagi, teorema Bayes secara matematis menghubungkan peluang kejadian A jika kejadian B dengan peluang B bila kejadian A.

Misalnya, jika Anda mengetahui terlebih dahulu kemungkinan seseorang akan menderita sakit kepala saat sedang flu, Anda dapat menggunakan teorema Bayes untuk menentukan kemungkinan seseorang akan terkena flu saat sedang sakit kepala.

Teorema Bayes memiliki banyak penerapan, misalnya digunakan dalam bidang kedokteran, ekonomi, atau teknologi untuk menghitung probabilitas kejadian tertentu karena kejadian lain. Di bawah ini, kita akan membahas secara rinci tentang berbagai penerapan teorema Bayes.

Teorema Bayes ditemukan oleh ahli matematika Inggris Thomas Bayes (1702-1761), meskipun diterbitkan secara anumerta pada tahun 1763.

➤ Lihat: Probabilitas bersyarat

Rumus teorema Bayes

Teorema Bayes mengatakan bahwa diberikan ruang sampel yang terdiri dari sekumpulan kejadian yang saling lepas {A ₁ , A ₂ ,…, A _i ,…, A _n } yang probabilitasnya tidak nol dan kejadian lain B , secara matematis kita dapat menghubungkan kondisional tersebut peluang A _i jika diberi kejadian B dengan peluang bersyarat B bila diberi A _i .

Jadi, rumus teorema Bayes yang disebut juga aturan Bayes adalah:

Emas:

$P(A_i|B)$

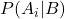
adalah peluang bersyarat dari kejadian A _i jika diberi kejadian B, disebut peluang posterior.
$P(B|A_i)$

adalah probabilitas bersyarat dari kejadian B pada kejadian tertentu A _i .
$P(A_i)$

adalah peluang terjadinya peristiwa A _i , disebut peluang apriori.

Perhatikan bahwa penyebut rumus teorema Bayes adalah probabilitas total kejadian B.

Contoh teorema Bayes

Setelah kita melihat definisi Teorema Bayes dan rumusnya, kita akan melihat contoh penyelesaian tentang bagaimana suatu probabilitas dihitung dengan Teorema Bayes untuk lebih memahami konsep tersebut.

Sebuah toko elektronik menjual tiga merek televisi: X, Y, Z. Diperkirakan 20% penjualannya adalah televisi merek cacat, 3% televisi merek Y cacat, dan 4% televisi merek Z cacat. Jika ada TV yang rusak, berapa probabilitas bahwa TV tersebut adalah TV Merek Z?

Latihan ini memberi kita probabilitas bahwa seorang pelanggan akan membeli setiap merek televisi:

Peristiwa A ₁ : Seorang pelanggan membeli televisi merek X → P(A ₁ )=0,20
Peristiwa A ₂ : Seorang pelanggan membeli televisi merek Y → P(A ₂ )=0,50
Peristiwa A ₃ : Seorang pelanggan membeli televisi merek Z → P(A ₃ )=0,30

Selain itu, pembacaan tersebut juga memberi kita kemungkinan bahwa televisi dari setiap merek rusak:

Peristiwa B: TV rusak

B|A ₁ : Diberikan televisi merek X, televisi tersebut rusak → P(B|A ₁ )=0,05
B|A ₂ : Diberi televisi merek Y, televisi tersebut rusak → P(B|A ₂ )=0,03
B|A ₃ : Diberi televisi merek Z, televisi tersebut rusak → P(B|A ₃ )=0,04

Jadi pohon probabilitas semua kejadian yang menarik perhatian kita adalah sebagai berikut:

Jadi, untuk menghitung probabilitas bahwa jika sebuah televisi rusak adalah merek Z, kita harus menggunakan rumus dari teorema Bayes:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

Menggunakan terminologi yang digunakan dalam contoh ini, rumus Bayes terlihat seperti ini:

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Jadi, perhitungan peluang suatu televisi cacat tertentu adalah merek Z adalah sebagai berikut:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}$

Kesimpulannya, probabilitas suatu televisi yang rusak adalah merek Z adalah 32%.

Penerapan teorema Bayes

Ada banyak penerapan teorema Bayes, antara lain:

Tes Medis : Teorema Bayes sering digunakan dalam kedokteran untuk menentukan kemungkinan lulus tes diagnostik. Misalnya, dalam kasus tes HIV, teorema tersebut dapat digunakan untuk menghitung probabilitas seseorang benar-benar mengidap virus jika hasil tesnya positif.
Analisis Keuangan : Di bidang keuangan, teorema Bayes digunakan untuk menghitung probabilitas terjadinya peristiwa ekonomi tertentu, seperti kenaikan atau penurunan nilai saham, dengan mempertimbangkan serangkaian variabel ekonomi.
Riset pasar : Teorema Bayes memungkinkan untuk menentukan, misalnya, kemungkinan seseorang akan membeli suatu produk setelah melihat iklan produk tersebut.
Prakiraan cuaca : Model cuaca juga menggunakan teorema Bayes untuk menentukan kemungkinan ramalan cuaca tertentu berdasarkan data pengamatan akan menjadi kenyataan. Hal ini meningkatkan keakuratan prakiraan iklim.
Keamanan Komputer – Dalam keamanan siber, teorema Bayes dapat diterapkan untuk menentukan kemungkinan bahwa aktivitas mencurigakan benar-benar merupakan serangan terhadap sistem komputer.

Menyelesaikan Masalah Teorema Bayes

Latihan 1

Diperkirakan 1% populasi menderita suatu penyakit. Tes untuk mendeteksi penyakit ini memiliki akurasi 95% untuk kasus positif dan 90% akurat untuk kasus negatif. Jika hasil tes seseorang yang dipilih secara acak positif, berapakah kemungkinan orang tersebut benar-benar mengidap penyakit tersebut?

Lihat solusinya

Pernyataan latihan memberi kita probabilitas berikut:

A ₁ : Orang tersebut mengidap penyakit → P(A ₁ )=0,01
A ₂ : Orang tersebut tidak menderita penyakit → P(A ₂ )=0,99

B: Tesnya positif
B|A ₁ : Tesnya positif bila orang tersebut mengidap penyakit → P(B|A ₁ )=0,95
B|A ₂ : Hasil tes positif bila orang tersebut tidak mengidap penyakit → P(B|A ₂ )=1-0.90=0.10

Kemudian, untuk menghitung probabilitas bahwa seseorang yang dipilih secara acak benar-benar mengidap penyakit tersebut ketika dites positif, aturan Bayes harus diterapkan:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}$

Jadi kami mengganti nilainya ke dalam rumus dan melakukan perhitungan probabilitas:

$\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}$

Singkatnya, kemungkinan seseorang yang dipilih secara acak dites positif dan benar-benar mengidap penyakit tersebut adalah 8,76%.

Latihan 2

Diperkirakan peluang suatu saham naik dalam satu hari adalah 40%, stabil 10%, dan turun 50%. Lebih jauh lagi, kita tahu bahwa ketika pasar naik, ada kemungkinan 90% bahwa seorang analis keuangan akan memprediksinya dengan benar, ketika pasar tetap stabil, kemungkinan prediksinya benar adalah 75% dan jika terjadi penurunan, kemungkinan prediksi yang benar adalah 75%. 85%.%. Jika seorang analis memperkirakan bahwa pasar akan jatuh, seberapa besar kemungkinan pasar akan benar-benar jatuh?

Lihat solusinya

Dalam hal ini, pernyataan latihan memberi kita probabilitas berikut:

A ₁ : Pasar naik dalam satu hari → P(A ₁ )=0,40
A ₂ : Pasar tetap stabil selama satu hari → P(A ₂ )=0,10
A ₃ : Pasar naik dalam satu hari → P(A ₃ )=0,50

B: Analis memperkirakan pasar akan jatuh
B|A ₁ : Analis memperkirakan dengan tepat bahwa pasar akan meningkat → P(B|A ₁ )=0.90
B|A ₂ : Analis memperkirakan dengan tepat bahwa pasar tetap stabil → P(B|A ₂ )=0.75
B|A ₃ : Analis memperkirakan dengan tepat bahwa pasar akan jatuh → P(B|A ₃ )=0.85

Untuk menentukan probabilitas seorang analis membuat prediksi bahwa pasar akan jatuh dan benar, kita perlu menggunakan rumus Teorema Bayes:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Kami mengganti nilai probabilitas ke dalam rumus Bayes dan menghitung probabilitasnya:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}$

Oleh karena itu, kemungkinan seorang analis benar ketika mengatakan bahwa pasar saham akan jatuh adalah 49,42%.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa teorema Bayes?

Rumus teorema Bayes

Contoh teorema Bayes

Penerapan teorema Bayes

Menyelesaikan Masalah Teorema Bayes

Latihan 1

Latihan 2

Tentang Penulis

Benjamin anderson

Tambahkan komentar