Teorema chebyshev

Oleh Benjamin anderson Agustus 5, 2023 Kemungkinan 0 Komentar

Artikel ini menjelaskan apa itu teorema Chebyshev. Di sini Anda akan menemukan rumus teorema Chebyshev, latihan yang diselesaikan, dan, sebagai tambahan, kalkulator teorema Chebyshev online. Terakhir, ini menunjukkan perbedaan antara teorema Chebyshev dan aturan empiris.

Apa teorema Chebyshev?

Teorema Chebyshev , juga dikenal sebagai pertidaksamaan Chebyshev , adalah aturan statistik yang digunakan untuk menghitung probabilitas suatu nilai variabel acak berada dalam jarak tertentu dari meannya.

Dengan kata lain, dalam statistik, teorema Chebyshev digunakan untuk menentukan probabilitas suatu nilai berada dalam interval kepercayaan.

Selain itu, teorema Chebyshev juga digunakan untuk membuktikan teorema statistik lainnya, seperti hukum bilangan besar.

Meskipun teorema Chebyshev pertama kali dirumuskan oleh orang Prancis Irénée-Jules Bienaymé, teorema ini dinamakan demikian karena berasal dari Pafnuty Chebushev dari Rusia pada tahun 1867.

Rumus teorema Chebyshev

Teorema Chebyshev mengatakan bahwa probabilitas suatu nilai sama dengan k standar deviasi dari mean lebih besar atau sama dengan satu dikurangi rasio satu dibagi k kuadrat.

Oleh karena itu, rumus teorema Chebyshev adalah sebagai berikut:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

Emas

$X$

adalah nilai variabel acak,

$\mu$

mean aritmatika dari variabel,

$\sigma$

deviasi standarnya dan

$k$

jumlah deviasi standar dari mean yang akan digunakan untuk menghitung probabilitas.

Perlu diperhatikan bahwa rumus ini hanya dapat digunakan jika jumlah simpangan baku yang dilakukan penghitungan lebih besar dari 1, atau dengan kata lain jika k lebih besar dari 1.

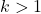$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ Anda dapat menggunakan kalkulator Teorema Chebyshev online di bawah ini untuk menghitung probabilitas.

Contoh teorema Chebyshev

Setelah kita melihat definisi teorema Chebyshev dan rumusnya, berikut adalah contoh penyelesaian teorema statistika untuk lebih memahami konsep tersebut.

Jika nilai yang diperoleh dalam statistik mata kuliah suatu universitas ditentukan oleh distribusi dengan rata-rata 65 dan deviasi standar 10, berapa persentase siswa yang memperoleh nilai antara 50 dan 80?

Untuk menyelesaikan masalah ini, kita perlu menerapkan rumus teorema Chebyshev. Namun kita harus menentukan terlebih dahulu berapa standar deviasi nilai 50 dan 80 dari mean variabel tersebut, untuk itu kita hanya perlu melakukan perhitungan sebagai berikut:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

Oleh karena itu, nilai 50 dan 80 masing-masing sesuai dengan 1,5 standar deviasi dari mean bawah dan atas. Oleh karena itu kami menggunakan rumus teorema Chebysheva dengan k=1,5:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

Dengan demikian, setidaknya 55,56% siswa memperoleh nilai antara 50 dan 80.

Kalkulator Teorema Chebyshev

Masukkan jumlah simpangan baku antara nilai yang dimaksud dengan mean (k) , lalu klik “Hitung”. Kalkulator kemudian akan mengembalikan probabilitas minimum dari interval kepercayaan.

Anda harus memasukkan jumlah simpangan baku menggunakan titik sebagai pemisah desimal.

Teorema dan aturan praktis Chebyshev

Dua konsep yang berkaitan erat dalam statistik adalah teorema Chebyshev dan aturan empiris, karena keduanya digunakan untuk menghitung probabilitas interval kepercayaan.

Perbedaan teorema Chebyshev dengan kaidah empiris adalah teorema Chebyshev dapat digunakan pada semua jenis distribusi, sedangkan kaidah empiris hanya berlaku untuk distribusi normal.

Oleh karena itu, penggunaan teorema Chebyshev lebih luas, tetapi aturan empiris memberikan hasil yang lebih tepat untuk distribusi normal.

Klik di sini untuk melihat aturan praktisnya:

➤ Lihat: aturan umum

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya