Tes breusch-pagan: definisi & contoh

Salah satu asumsi utama regresi linier adalah bahwa residu terdistribusi dengan varian yang sama di setiap tingkat variabel prediktor. Asumsi ini dikenal dengan istilah homoskedastisitas .

Jika asumsi ini tidak dipenuhi, maka dikatakan terdapat heteroskedastisitas pada residu. Jika hal ini terjadi, hasil regresi menjadi tidak dapat diandalkan.

Salah satu cara untuk mendeteksi secara visual apakah terdapat heteroskedastisitas adalah dengan membuat plot residu terhadap nilai yang sesuai dari model regresi.

Jika residu semakin menyebar pada nilai grafik yang lebih tinggi, hal ini merupakan tanda adanya heteroskedastisitas.

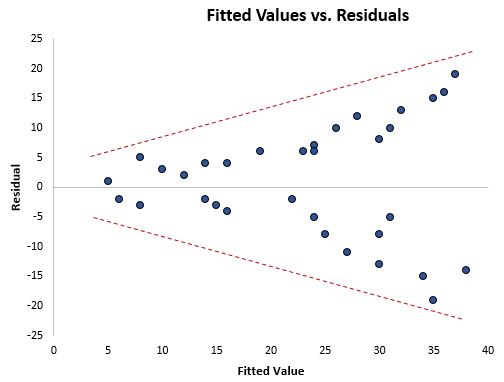
Uji statistik formal yang dapat kita gunakan untuk mengetahui ada tidaknya heteroskedastisitas adalah uji Breusch-Pagan .

Tutorial ini memberikan penjelasan singkat tentang tes Breusch-Pagan beserta contohnya.

Apa tes Breusch-Pagan?

Uji Breusch-Pagan digunakan untuk mengetahui ada atau tidaknya heteroskedastisitas dalam suatu model regresi.

Pengujian ini menggunakan hipotesis nol dan hipotesis alternatif berikut:

• Hipotesis nol (H ₀ ): terdapat homoskedastisitas (residu terdistribusi dengan varian yang sama)
• Hipotesis alternatif ( _HA ): terdapat heteroskedastisitas (sisa tidak terdistribusi dengan varian yang sama)

Jika nilai p dari uji tersebut berada di bawah tingkat signifikansi tertentu (yaitu, α = 0,05), maka kami menolak hipotesis nol dan menyimpulkan bahwa terdapat heteroskedastisitas dalam model regresi.

Kami menggunakan langkah-langkah berikut untuk melakukan tes Breusch-Pagan:

1. Sesuaikan model regresi.

2. Hitung kuadrat sisa model.

3. Cocokkan model regresi baru, dengan menggunakan kuadrat residu sebagai nilai respons.

4. Hitung statistik uji Chi-kuadrat X ² dalam bentuk n*R ² _baru dimana:

• n : Jumlah total observasi
• R ² _baru : R kuadrat model regresi baru yang menggunakan kuadrat residu sebagai nilai respons

Jika nilai p yang sesuai dengan statistik uji chi-kuadrat ini dengan derajat kebebasan p (jumlah prediktor) berada di bawah tingkat signifikansi tertentu (yaitu α = 0,05), maka tolak hipotesis nol dan simpulkan bahwa terdapat heteroskedastisitas. .

Jika tidak, jangan menolak hipotesis nol. Dalam hal ini diasumsikan ada homoskedastisitas.

Perhatikan bahwa sebagian besar perangkat lunak statistik dapat dengan mudah melakukan uji Breusch-Pagan, jadi Anda mungkin tidak perlu melakukan langkah-langkah ini secara manual, namun mengetahui apa yang terjadi di balik layar akan sangat membantu.

Contoh tes Breusch-Pagan

Misalkan kita memiliki kumpulan data berikut yang berisi informasi tentang 10 pemain bola basket berbeda:

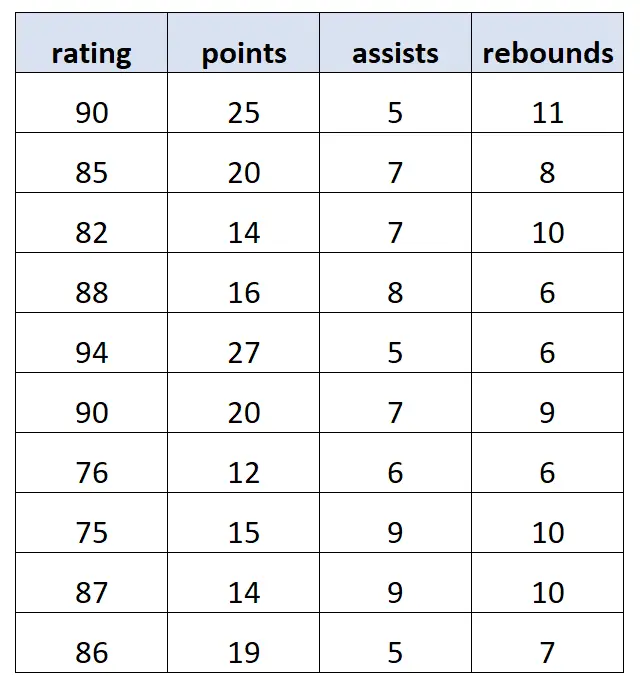
Dengan menggunakan perangkat lunak statistik, kami menyesuaikan model regresi linier berganda berikut:

skor = 62,47 + 1,12*(poin) + 0,88*(assist) – 0,43*(rebound)

Kami kemudian menggunakan model ini untuk membuat prediksi tentang peringkat masing-masing pemain dan menghitung sisa kuadrat (yaitu selisih kuadrat antara peringkat yang diprediksi dan peringkat sebenarnya):

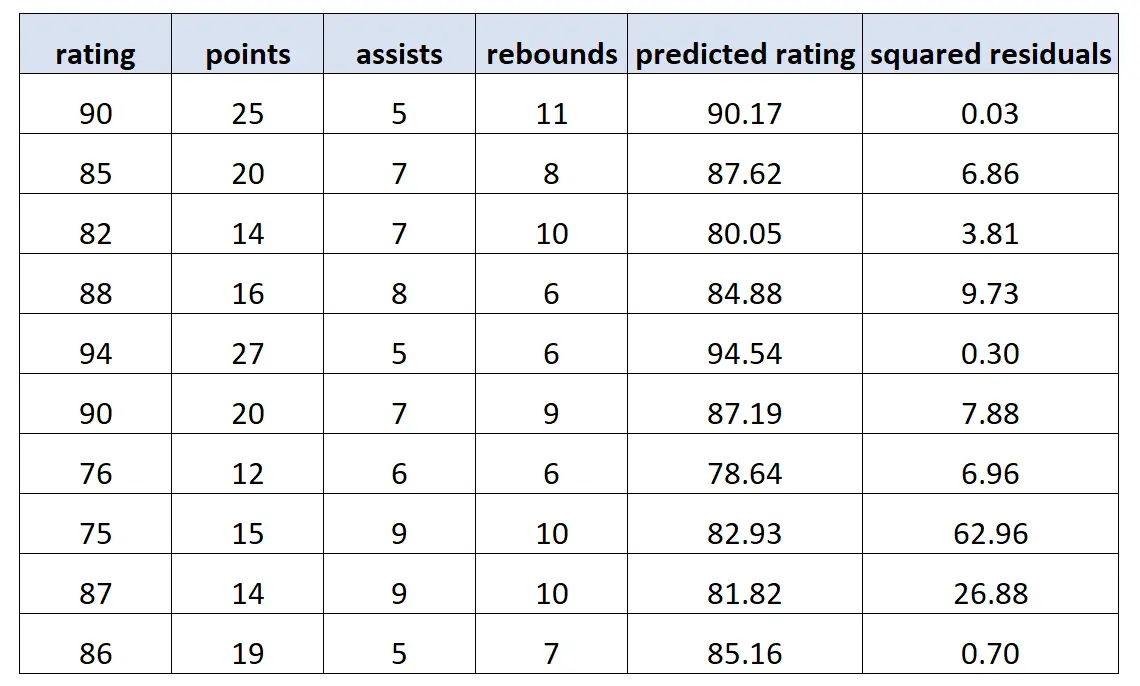
Selanjutnya, kami memasang model regresi baru dengan menggunakan kuadrat residu sebagai nilai respons dan sekali lagi variabel prediktor asli sebagai variabel prediktor. Kami menemukan hal berikut:

• n: 10
• R ² _baru : 0,600395

Jadi, statistik uji Chi-kuadrat kami untuk uji Breusch-Pagan adalah n*R ² _new = 10*.600395 = 6.00395 . Derajat kebebasannya adalah p = 3 variabel prediktor.

Menurut kalkulator nilai chi kuadrat ke P , nilai p yang sesuai dengan X ² = 6,00395 dengan 3 derajat kebebasan adalah 0,111418 .

Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Oleh karena itu kami berasumsi bahwa ada homoskedastisitas.

Tes Breusch-Pagan dalam praktiknya

Tutorial berikut memberikan contoh langkah demi langkah tentang cara melakukan uji Breusch-Pagan di berbagai program statistik:

Cara Melakukan Tes Breusch-Pagan di Excel
Cara melakukan tes Breusch-Pagan di R
Cara melakukan tes Breusch-Pagan dengan Python
Cara melakukan tes Breusch-Pagan di Stata