Cara melakukan uji chi kuadrat dengan tangan (langkah demi langkah)
Uji kesesuaian chi-kuadrat digunakan untuk menentukan apakah suatu variabel kategori mengikuti distribusi hipotetis atau tidak.
Contoh langkah demi langkah berikut menunjukkan cara melakukan uji kesesuaian chi-kuadrat secara manual.
Uji kesesuaian chi-kuadrat dengan tangan
Misalkan kita yakin bahwa suatu dadu tertentu benar. Dengan kata lain, kami percaya bahwa dadu memiliki peluang yang sama untuk mendarat pada angka 1, 2, 3, 4, 5, atau 6 pada pelemparan tertentu.
Untuk mengujinya, kami melemparkannya sebanyak 60 kali dan mencatat nomor yang dilemparnya setiap kali. Hasilnya adalah sebagai berikut:
- 1 :8 kali
- 2 : 12 kali
- 3 : 18 kali
- 4 :9 kali
- 5 :7 kali
- 6 : 6 kali
Ikuti langkah-langkah berikut untuk melakukan uji kesesuaian chi-kuadrat untuk menentukan apakah dadunya adil.
Langkah 1: Tentukan hipotesis nol dan hipotesis alternatif
- H 0 (null): dadu mempunyai peluang yang sama untuk mendarat pada setiap angka.
- H 1 (alternatif): Peluang mendaratnya dadu pada setiap nomor tidak sama.
Langkah 2: Hitung frekuensi yang diamati dan yang diharapkan
Selanjutnya, mari kita buat tabel frekuensi yang diamati dan diharapkan untuk setiap angka pada dadu:
Catatan : Jika menurut kami dadu tersebut adil, artinya kami memperkirakan dadu akan mendarat di setiap angka dengan jumlah yang sama – dalam hal ini, masing-masing 10 kali.
Langkah 3: Hitung statistik pengujian
Statistik uji Chi-kuadrat, X 2 , dihitung sebagai berikut:
- X 2 = (OE) 2 / E
Tabel berikut menunjukkan cara menghitung statistik pengujian ini:
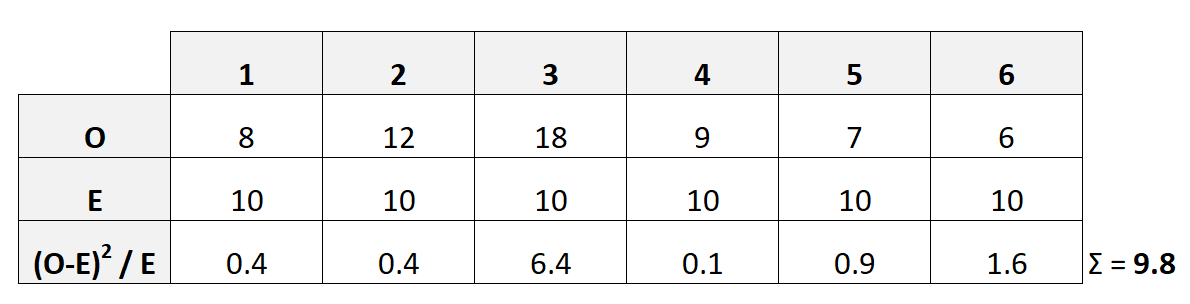
Dalam hal ini, X 2 ternyata 9.8 .
Langkah 4: Temukan nilai kritisnya
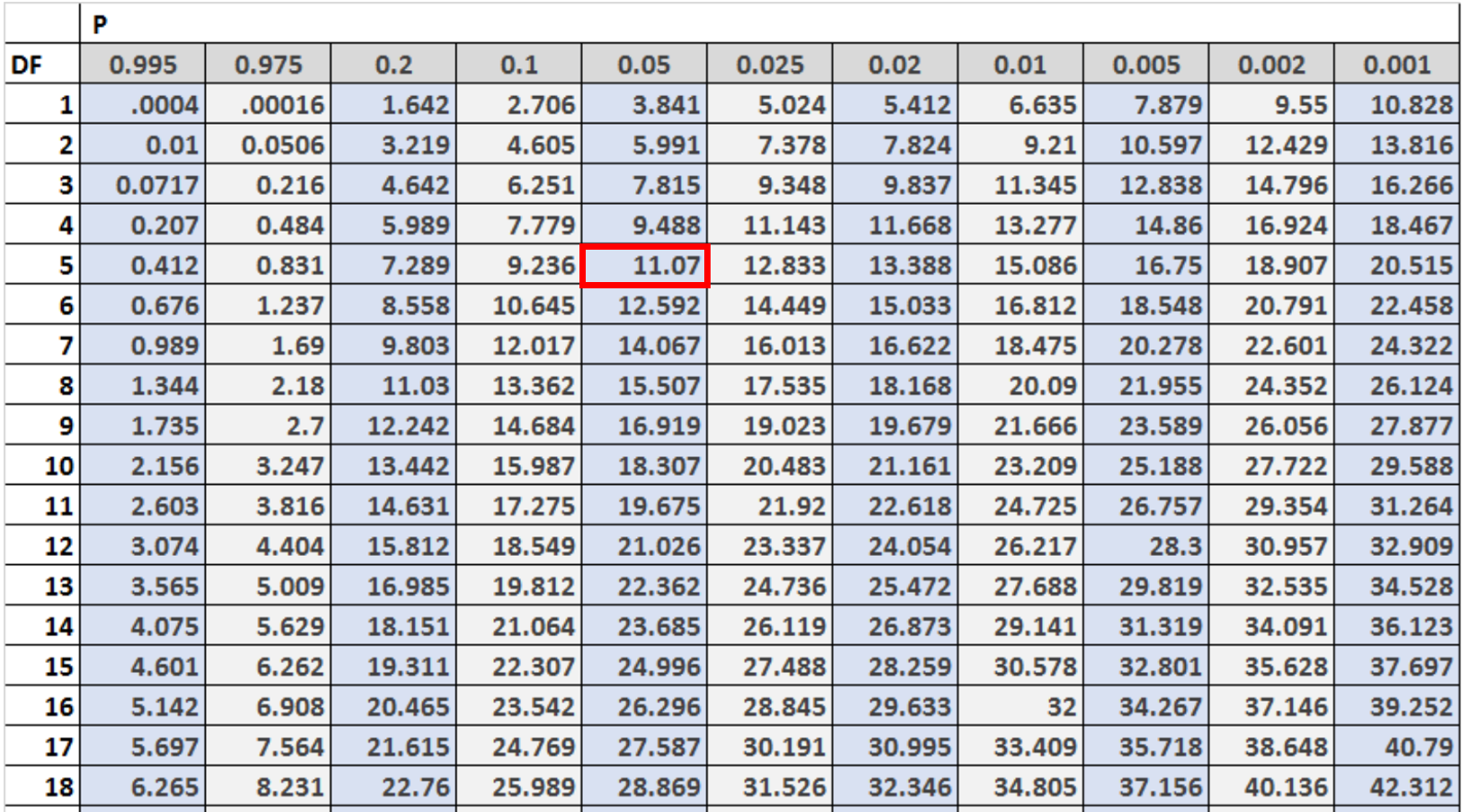
Selanjutnya, kita perlu mencari nilai kritis pada tabel distribusi Chi-kuadrat yang sesuai dengan α = 0,05 dan df = (#kategori – 1).
Dalam hal ini ada 6 kategori, jadi kita akan menggunakan df = 6 – 1 = 5 .
Kita dapat melihat bahwa nilai kritisnya adalah 11.07 .
Langkah 5: Tolak atau gagal menolak hipotesis nol
Karena statistik pengujian kami kurang dari nilai kritis, kami gagal menolak hipotesis nol. Ini berarti kita tidak memiliki cukup bukti untuk mengatakan bahwa dadu tersebut tidak adil.
Sumber daya tambahan
Sumber daya berikut menawarkan informasi tambahan tentang uji kesesuaian chi-kuadrat:
Pengantar uji kesesuaian chi-kuadrat
Cara melakukan uji kesesuaian chi-kuadrat di R
Kalkulator uji kecocokan chi-kuadrat
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya