Bagaimana melakukan tes dunnett di r

Tes post hoc adalah jenis tes yang dilakukan mengikuti ANOVA untuk menentukan mean kelompok mana yang secara statistik berbeda secara signifikan satu sama lain.

Jika salah satu kelompok belajar dianggap sebagai kelompok kontrol , maka kita harus menggunakan uji Dunnett sebagai tes post-hoc.

Tutorial ini menjelaskan cara melakukan tes Dunnett di R.

Contoh: Tes Dunnett di R

Misalkan seorang guru ingin mengetahui apakah dua teknik belajar baru mempunyai potensi untuk meningkatkan nilai ujian siswanya. Untuk mengujinya, dia secara acak membagi kelasnya yang terdiri dari 30 siswa menjadi tiga kelompok berikut:

• Kelompok kontrol: 10 siswa
• Studi teknis baru 1: 10 siswa
• Studi teknis baru 2: 10 siswa

Setelah seminggu menggunakan teknik belajar yang ditugaskan kepada mereka, setiap siswa mengikuti ujian yang sama.

Kita dapat menggunakan langkah-langkah berikut dalam R untuk membuat kumpulan data, memvisualisasikan rata-rata kelompok, melakukan ANOVA satu arah, dan terakhir melakukan uji Dunnett untuk menentukan teknik studi baru mana (jika ada) yang menghasilkan hasil berbeda jika dibandingkan dengan kelompok kontrol. .

Langkah 1: Buat kumpulan data.

Kode berikut menunjukkan cara membuat kumpulan data yang berisi hasil ujian seluruh 30 siswa:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Langkah 2: Lihat hasil ujian untuk setiap kelompok.

Kode berikut menunjukkan cara membuat diagram kotak untuk memvisualisasikan sebaran hasil ujian tiap kelompok:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

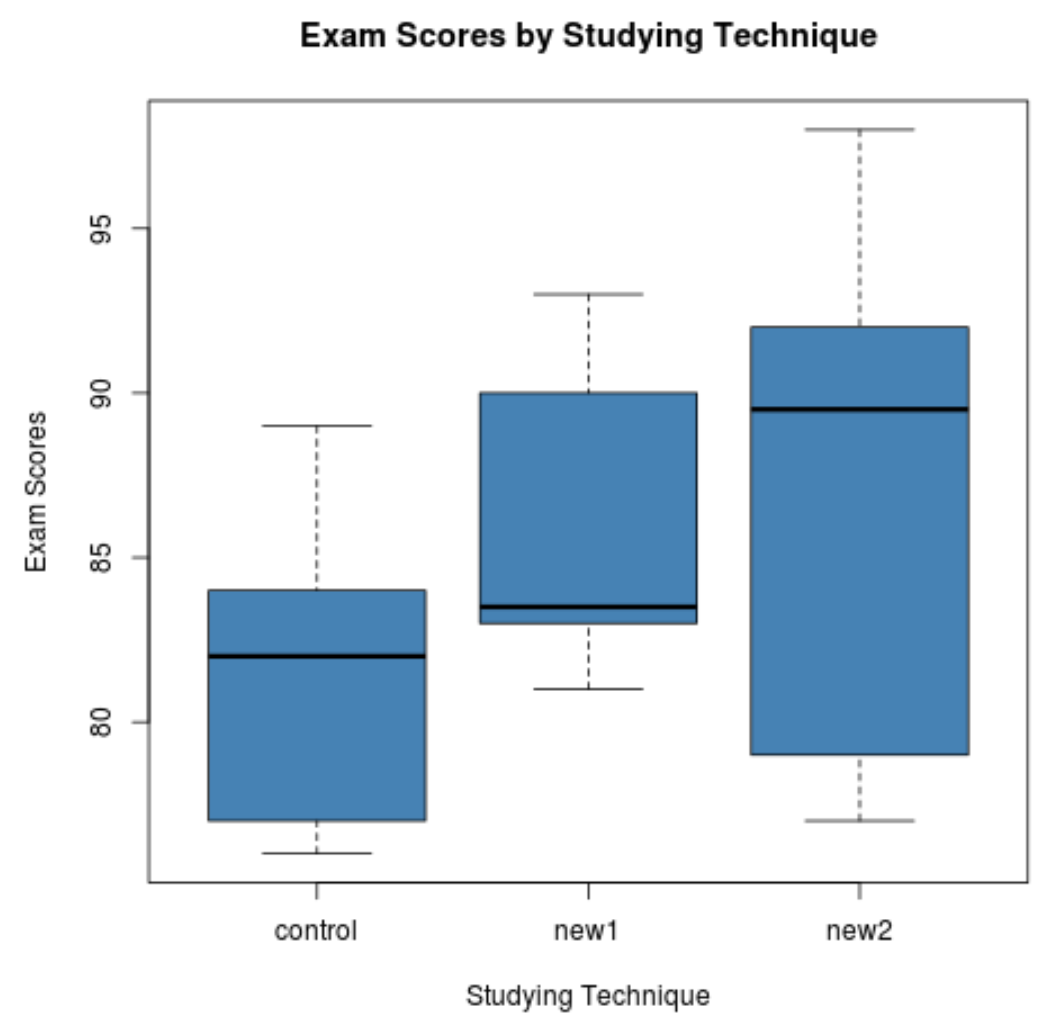
Dari box plot saja kita dapat melihat bahwa sebaran nilai ujian untuk setiap teknik pembelajaran sangat berbeda-beda. Kami kemudian akan melakukan ANOVA satu arah untuk menentukan apakah perbedaan ini signifikan secara statistik.

Terkait: Cara Membuat Plot Beberapa Plot Kotak dalam Satu Bagan di R

Langkah 3: Lakukan ANOVA satu arah.

Kode berikut menunjukkan cara melakukan ANOVA satu arah untuk menguji perbedaan antara rata-rata nilai ujian di setiap kelompok:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Karena nilai p keseluruhan ( 0,0476 ) kurang dari 0,05, hal ini menunjukkan bahwa setiap kelompok tidak memiliki rata-rata nilai ujian yang sama. Selanjutnya, kita akan melakukan tes Dunnett untuk menentukan teknik belajar mana yang menghasilkan rata-rata nilai ujian yang berbeda dari rata-rata nilai ujian kelompok kontrol.

Langkah 4: Lakukan tes Dunnett.

Untuk melakukan pengujian Dunnett di R kita dapat menggunakan fungsi DunnettTest() dari perpustakaan DescTools yang menggunakan sintaks berikut:

Tes Dunnett (x, g)

Emas:

• x: vektor numerik dari nilai data (misalnya hasil ujian)
• g: Vektor yang menentukan nama kelompok (misalnya teknik belajar)

Kode berikut menunjukkan cara menggunakan fungsi ini untuk contoh kita:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

Cara menafsirkan hasilnya adalah sebagai berikut:

• Rata-rata selisih nilai ujian antara teknik belajar baru 1 dan kelompok kontrol adalah 4,2. Nilai p yang sesuai adalah 0,1787 .
• Rata-rata selisih nilai ujian antara teknik belajar baru 2 dengan kelompok kontrol adalah 6,4. Nilai p yang sesuai adalah 0,0296 .

Berdasarkan hasil, kita dapat melihat bahwa mempelajari Teknik 2 adalah satu-satunya teknik yang menghasilkan nilai rata-rata ujian yang berbeda secara signifikan (p = 0,0296) dibandingkan dengan kelompok kontrol.

Sumber daya tambahan

Pengantar ANOVA Satu Arah
Bagaimana melakukan ANOVA satu arah di R
Cara melakukan tes Tukey di R