Apa itu tes makanan? (penjelasan & contoh)

Uji Chow adalah uji statistik yang dikembangkan oleh ekonom Gregory Chow yang digunakan untuk menguji apakah koefisien dua model regresi berbeda pada kumpulan data berbeda adalah sama.

Uji Chow biasanya digunakan dalam bidang ekonometrika dengan data deret waktu untuk menentukan apakah terdapat kerusakan struktural pada data pada suatu titik waktu tertentu.

Misalnya, pertimbangkan plot sebar berikut:

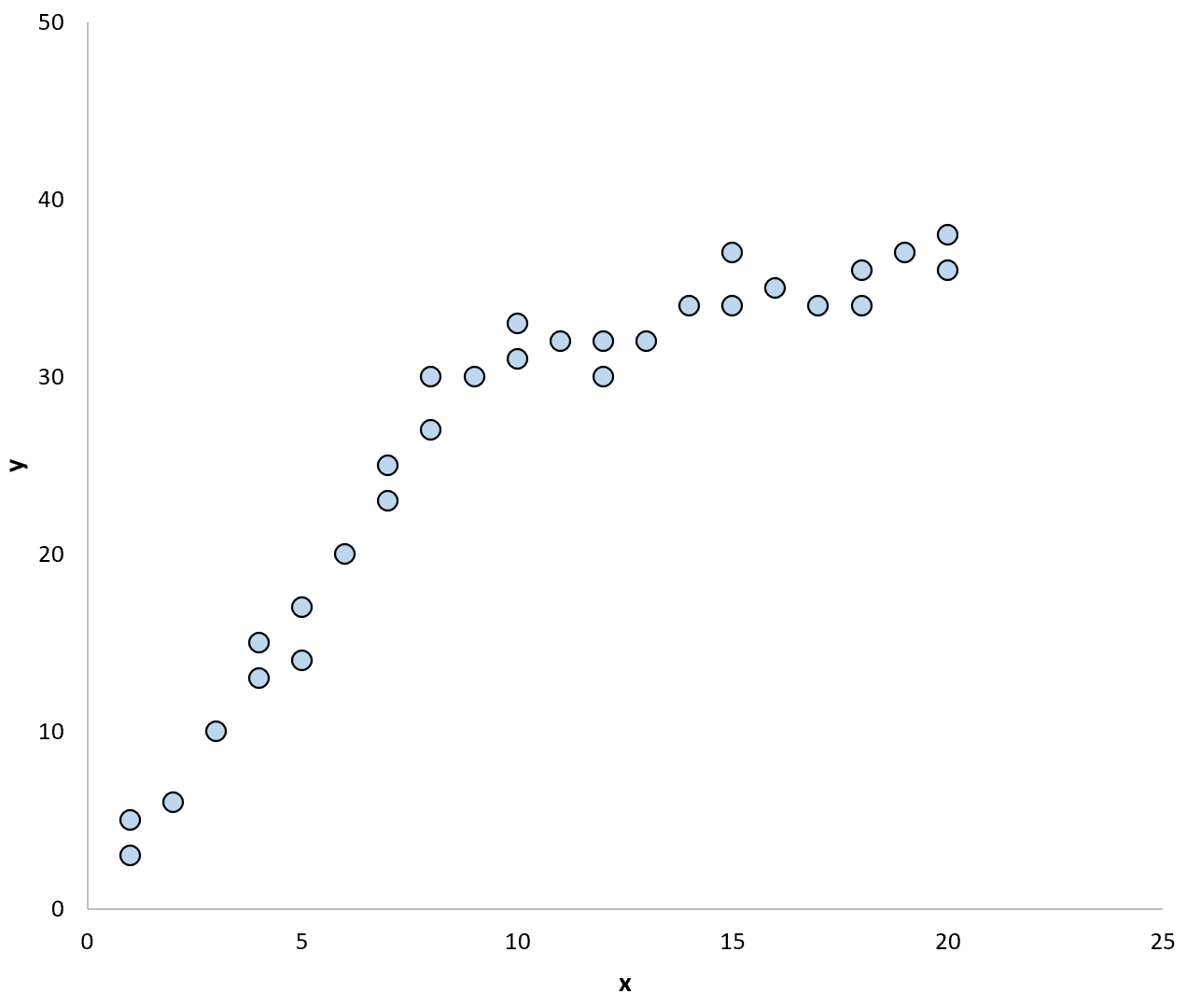
Jika kita menggunakan garis regresi untuk meringkas model dalam data, tampilannya akan seperti ini:

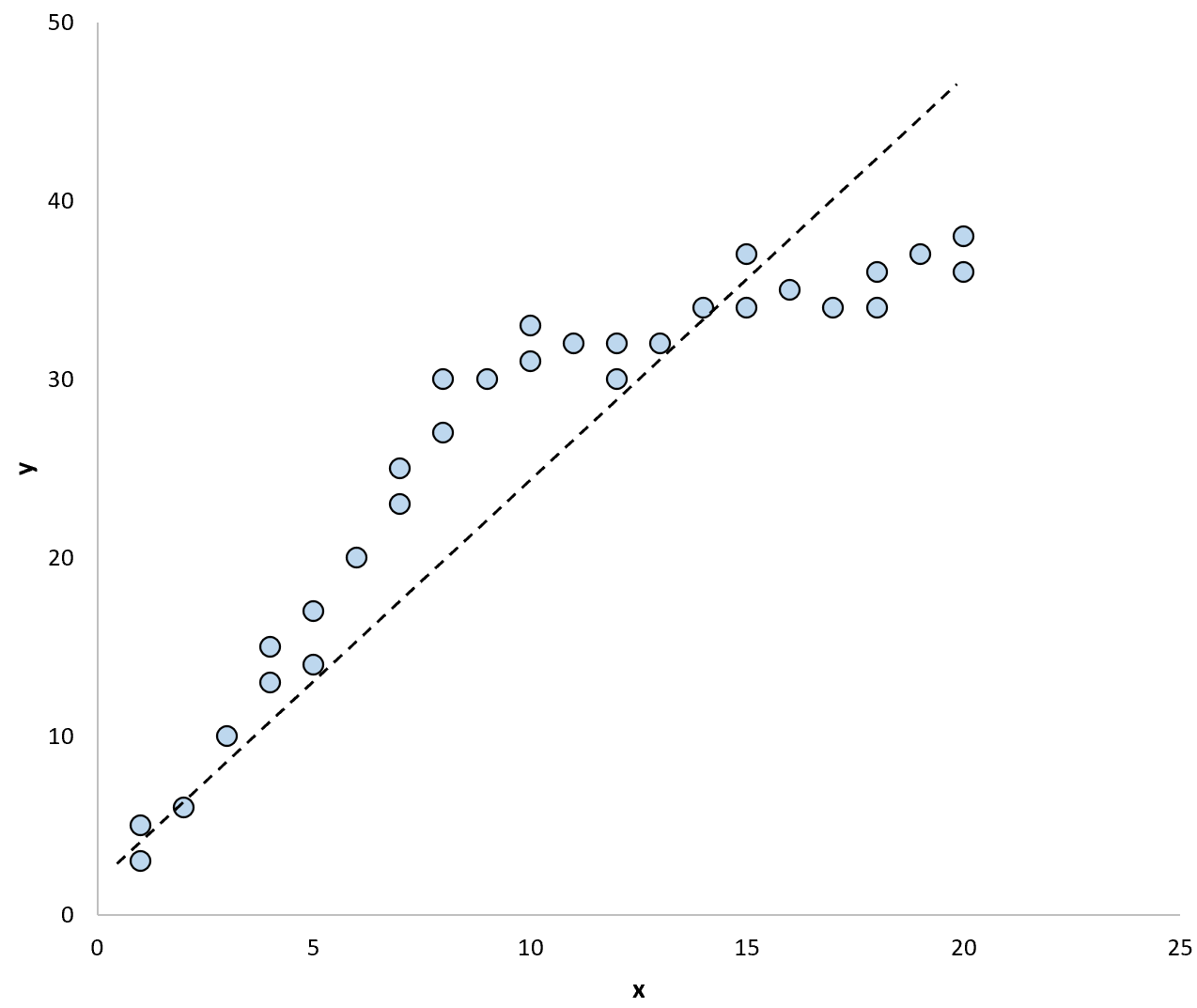
Dan jika kita menggunakan dua garis regresi terpisah untuk meringkas model dalam data, tampilannya akan seperti ini:

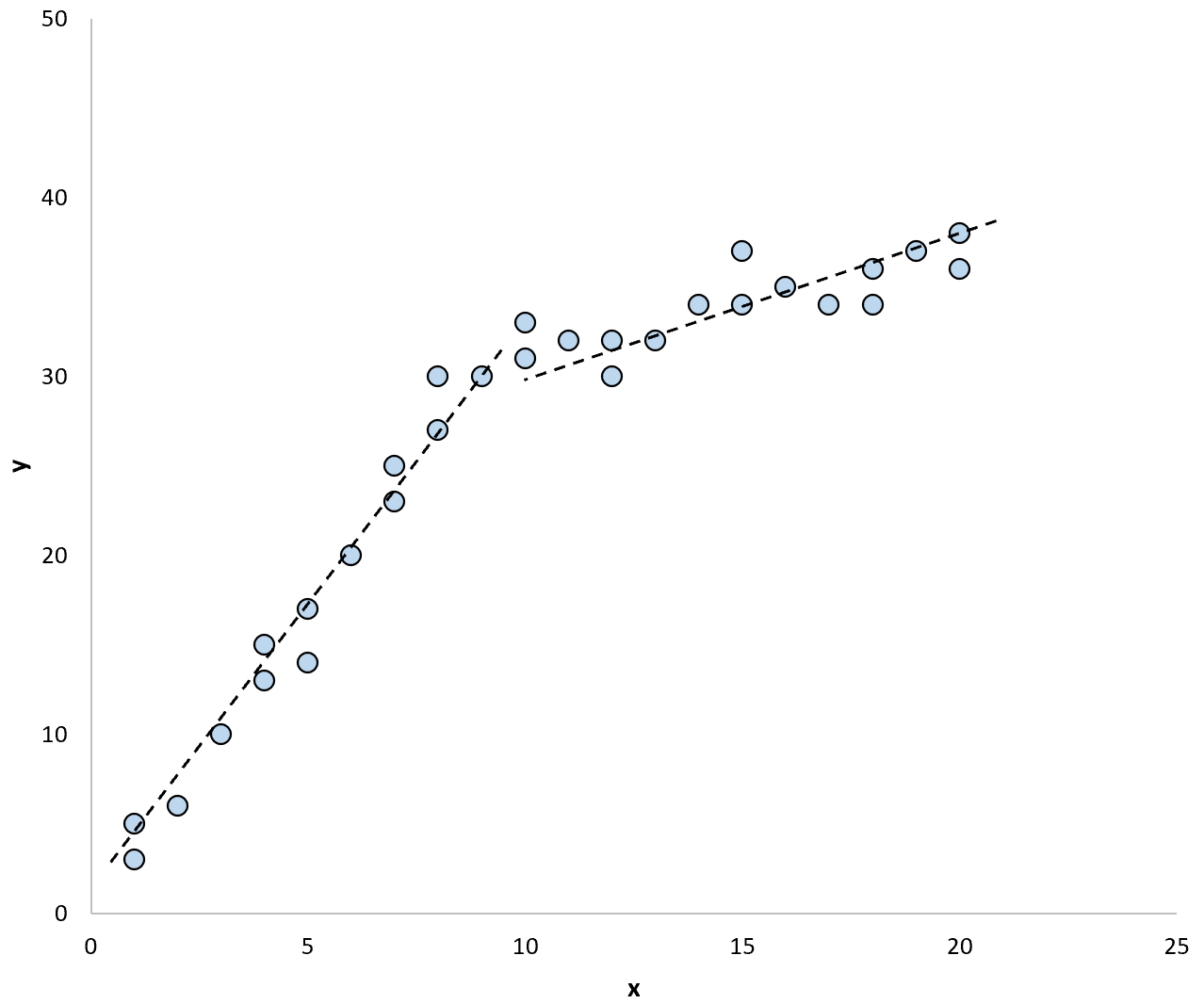
Uji Chow memungkinkan kita menguji apakah koefisien regresi setiap garis regresi sama atau tidak.

Jika pengujian menunjukkan bahwa koefisien antar garis regresi tidak sama, hal ini berarti terdapat bukti signifikan adanya kerusakan struktural pada data. Dengan kata lain, tren data sebelum dan sesudah break point struktural ini sangat berbeda.

Kapan menggunakan tes Chow

Contoh berikut menggambarkan situasi di mana Anda mungkin ingin melakukan tes Chow:

1. Tentukan apakah harga saham bergerak pada tingkat yang berbeda sebelum dan sesudah pemilu.

2. Menentukan apakah harga rumah berubah sebelum dan sesudah perubahan suku bunga.

3. Menentukan apakah rata-rata keuntungan perusahaan publik sebelum dan sesudah penerapan undang-undang perpajakan baru berbeda.

Dalam setiap situasi, kita dapat menggunakan uji Chow untuk menentukan apakah terdapat titik putus struktural dalam data pada waktu tertentu.

Langkah-Langkah Melakukan Tes Chow

Kita dapat menggunakan langkah-langkah berikut untuk melakukan tes Chow.

Langkah 1: Tentukan hipotesis nol dan hipotesis alternatif.

Misalkan kita menyesuaikan model regresi berikut ke seluruh kumpulan data kita:

• kamu _t = a + bx _1t + cx _t2 + ε

Selanjutnya, misalkan kita membagi data menjadi dua kelompok berdasarkan breakpoint struktural dan menyesuaikan model regresi berikut untuk setiap kelompok:

• _yt = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• kamu _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Kami akan menggunakan hipotesis nol dan alternatif berikut untuk uji Chow:

• Null (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ dan c ₁ = c ₂
• Alternatif ( _HA ): Setidaknya salah satu perbandingan di Null tidak sama.

Jika kita menolak hipotesis nol, kita mempunyai cukup bukti untuk mengatakan bahwa terdapat titik putus struktural dalam data dan bahwa dua garis regresi dapat lebih cocok dengan data daripada satu.

Jika kita gagal menolak hipotesis nol, kita tidak memiliki cukup bukti untuk mengatakan bahwa terdapat titik putus struktural dalam data. Dalam hal ini, kita katakan bahwa garis regresi dapat “disatukan” menjadi satu garis regresi yang mewakili pola data dengan cukup baik.

Langkah 2: Hitung statistik pengujian.

Jika kita mendefinisikan istilah-istilah berikut:

• S _T : Jumlah kuadrat sisa dari total data
• S ₁ , S ₂ : jumlah kuadrat sisa masing-masing kelompok
• N ₁ , N ₂ : Banyaknya observasi pada setiap kelompok
• k : Jumlah parameter

Kemudian kita dapat mengatakan bahwa statistik uji Chow adalah:

Statistik uji chow = [( _ST – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Statistik uji ini mengikuti distribusi F dengan k dan dan N ₁ +N ₂ -2k derajat kebebasan.

Langkah 3: Tolak atau jangan tolak hipotesis nol.

Jika nilai p yang terkait dengan statistik uji ini berada di bawah tingkat signifikansi tertentu, kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat titik putus struktural dalam data.

Untungnya, sebagian besar perangkat lunak statistik mampu melakukan pengujian Chow, jadi Anda mungkin tidak perlu melakukan pengujian secara manual.

Contoh melakukan tes Chow

Lihat tutorial ini untuk melihat contoh langkah demi langkah tentang cara melakukan pengujian Chow untuk kumpulan data tertentu di R.

Catatan Tes Chow

Berikut beberapa catatan yang perlu diingat tentang tes Chow:

1. Pengujian mengasumsikan bahwa residu model regresi terdistribusi secara independen dan identik dari distribusi normal dengan varians yang tidak diketahui.

2. Uji Chow hanya boleh digunakan jika kerusakan struktural yang ingin Anda uji terjadi pada waktu yang diketahui . Dengan kata lain, pengujian tidak boleh digunakan berulang kali untuk menentukan apakah suatu momen tertentu dapat dianggap sebagai kerusakan struktural.