Cara melakukan tes shapiro-wilk di r (dengan contoh)

Uji Shapiro-Wilk merupakan uji normalitas. Ini digunakan untuk menentukan apakah suatu sampel berasal dari distribusi normal atau tidak.

Jenis pengujian ini berguna untuk menentukan apakah suatu kumpulan data berasal dari distribusi normal atau tidak, yang merupakan asumsi yang umum digunakan dalam banyak pengujian statistik, termasuk regresi , ANOVA , uji-t , dan banyak lainnya. ‘yang lain.

Kita dapat dengan mudah melakukan pengujian Shapiro-Wilk pada kumpulan data tertentu menggunakan fungsi bawaan berikut di R:

shapiro.test(x)

Emas:

• x: vektor numerik dari nilai data.

Fungsi ini menghasilkan statistik uji W bersama dengan nilai p yang sesuai. Jika p-value kurang dari α = 0,05, terdapat cukup bukti untuk mengatakan bahwa sampel tersebut bukan berasal dari populasi yang berdistribusi normal.

Catatan: Ukuran sampel harus antara 3 dan 5.000 untuk menggunakan fungsi shapiro.test().

Tutorial ini menunjukkan beberapa contoh penggunaan praktis fungsi ini.

Contoh 1: Uji Shapiro-Wilk pada data normal

Kode berikut menunjukkan cara melakukan pengujian Shapiro-Wilk pada kumpulan data dengan ukuran sampel n=100:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

Nilai p dari tes tersebut ternyata 0,6303 . Karena nilai ini tidak kurang dari 0,05, maka kita dapat berasumsi bahwa data sampel berasal dari populasi yang berdistribusi normal.

Hasil ini seharusnya tidak mengejutkan karena kami membuat data sampel menggunakan fungsi rnorm(), yang menghasilkan nilai acak dari distribusi normal dengan mean = 0 dan standar deviasi = 1.

Terkait: Panduan untuk dnorm, pnorm, qnorm dan rnorm di R

Kami juga dapat membuat histogram untuk memverifikasi secara visual bahwa data sampel terdistribusi secara normal:

 hist(data, col=' steelblue ') 

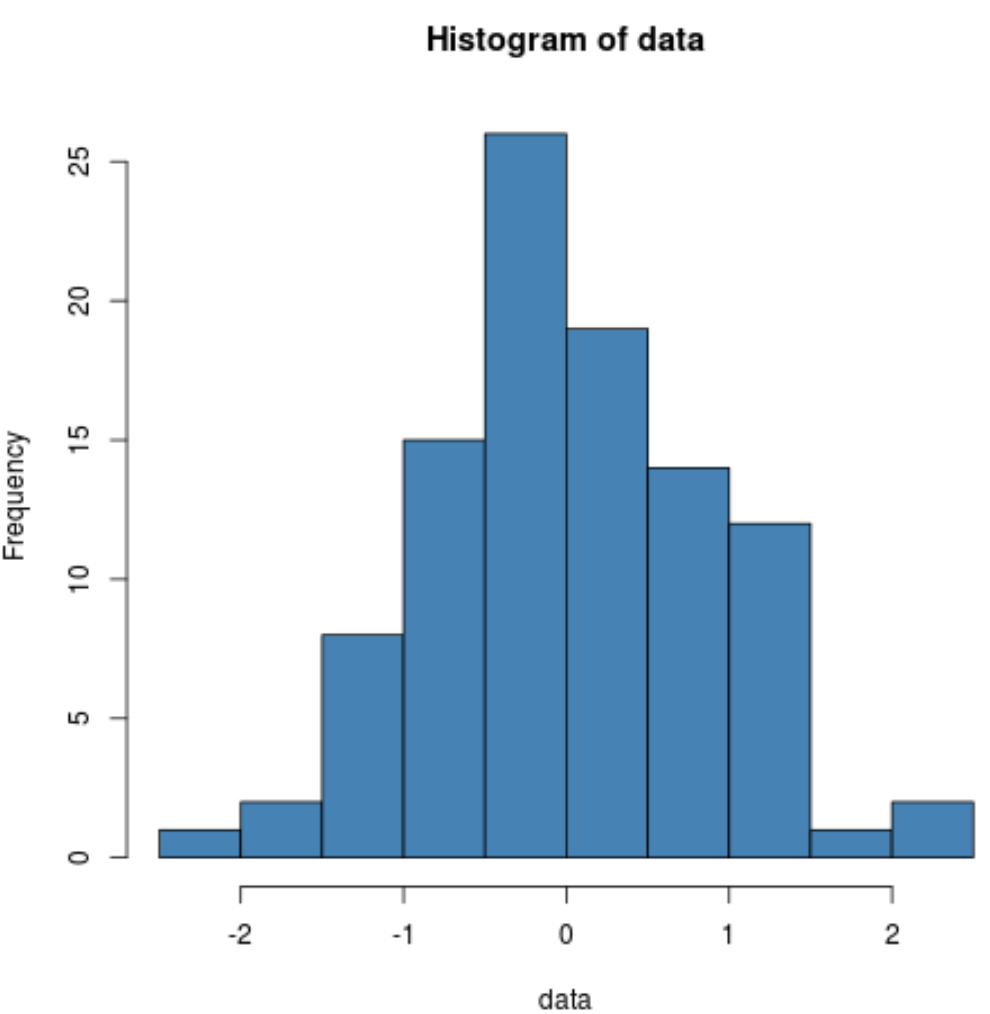
Kita dapat melihat bahwa distribusinya berbentuk lonceng dengan puncak di tengah distribusi, yang merupakan ciri khas dari data yang berdistribusi normal.

Contoh 2: Uji Shapiro-Wilk pada data tidak normal

Kode berikut menunjukkan cara melakukan pengujian Shapiro-Wilk pada dataset dengan ukuran sampel n=100 yang nilainya dihasilkan secara acak dari distribusi Poisson :

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

Nilai p dari tes tersebut ternyata 0,0003393 . Karena nilai ini kurang dari 0,05, kita mempunyai cukup bukti untuk mengatakan bahwa data sampel tidak berasal dari populasi yang berdistribusi normal.

Hasil ini seharusnya tidak mengejutkan karena kami membuat data sampel menggunakan fungsi rpois(), yang menghasilkan nilai acak dari distribusi Poisson.

Terkait: Panduan untuk dpois, ppois, qpois, dan rpois di R

Kita juga dapat membuat histogram untuk melihat secara visual bahwa data sampel tidak terdistribusi secara normal:

 hist(data, col=' coral2 ') 

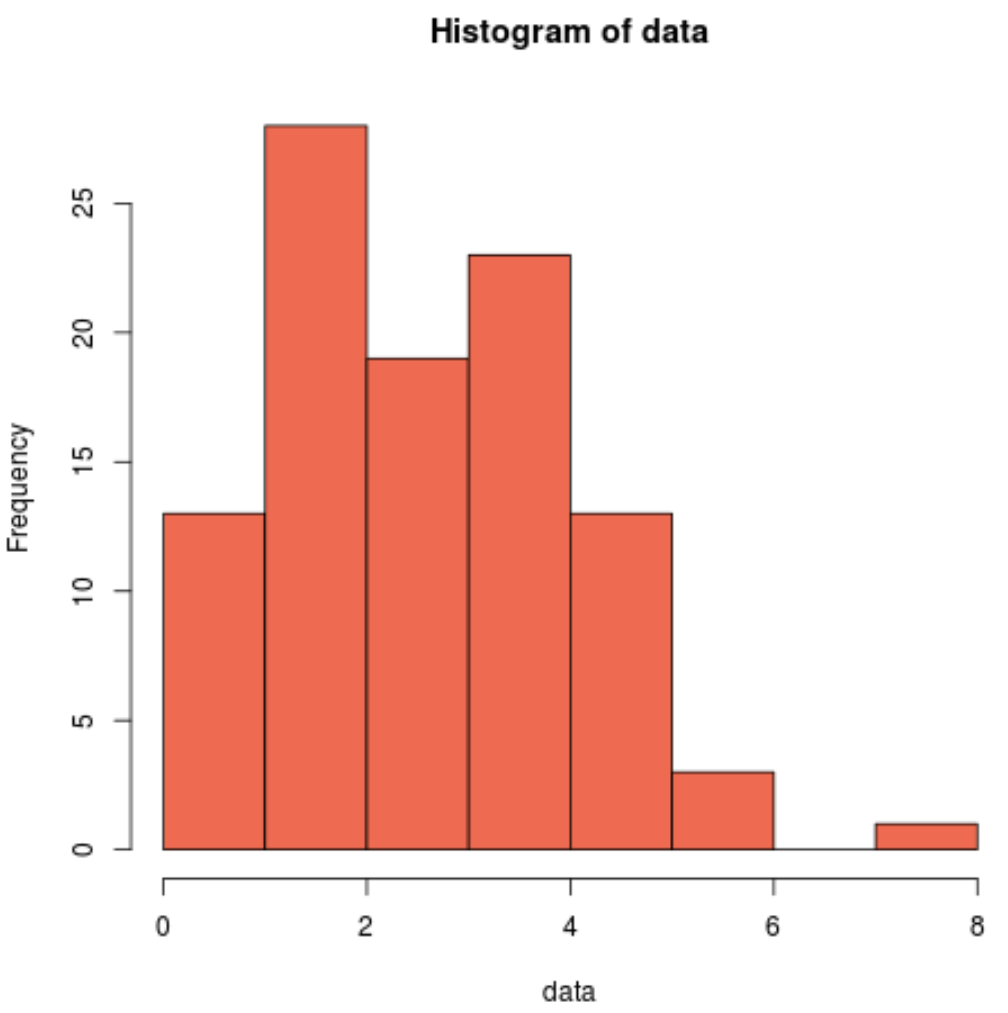
Kita dapat melihat bahwa distribusinya miring ke kanan dan tidak memiliki “bentuk lonceng” khas yang diasosiasikan dengan distribusi normal. Dengan demikian, histogram kami cocok dengan hasil uji Shapiro-Wilk dan menegaskan bahwa data sampel kami tidak berasal dari distribusi normal.

Apa yang harus dilakukan dengan data yang tidak normal

Jika kumpulan data tertentu tidak terdistribusi secara normal, kita sering kali dapat melakukan salah satu transformasi berikut untuk membuatnya lebih normal:

1. Transformasi log: ubah variabel respons dari y menjadi log(y) .

2. Transformasi akar kuadrat: Transformasikan variabel respon dari y menjadi √y .

3. Transformasi akar pangkat tiga: ubah variabel respon dari y menjadi y ^1/3 .

Dengan melakukan transformasi ini, variabel respon secara umum mendekati distribusi normal.

Lihat tutorial ini untuk melihat cara melakukan transformasi ini dalam praktiknya.

Sumber daya tambahan

Cara melakukan tes Anderson-Darling di R
Cara melakukan tes Kolmogorov-Smirnov di R
Cara Melakukan Tes Shapiro-Wilk dengan Python