Uji-t siswa
Artikel ini menjelaskan apa itu uji Student t dan kegunaannya dalam statistik. Dengan demikian, Anda akan mengetahui cara pelaksanaan uji t Student, apa saja jenis uji t Student, dan rumus masing-masingnya.
Berapakah uji-t Student?
Uji-t Student , disebut juga Uji-T atau sederhananya Uji-t , adalah uji statistik yang statistik pengujiannya mengikuti distribusi-t Student . Oleh karena itu, dalam statistika, uji-t Student digunakan untuk menolak atau menerima hipotesis nol suatu uji hipotesis.
Secara khusus, uji-t Student digunakan dalam pengujian hipotesis dimana populasi yang diteliti mengikuti distribusi normal, namun ukuran sampel terlalu kecil untuk mengetahui varians populasi.
Singkatnya, uji-t Student digunakan untuk menolak atau menerima hipotesis penelitian dari uji hipotesis tertentu. Misalnya, uji-t Student digunakan untuk menguji hipotesis pada satu sampel, pada sampel independen, atau pada sampel terkait. Kita kemudian akan melihat bagaimana uji t Student dihitung dalam setiap kasus.
Jenis uji-t Siswa
Ada tiga jenis uji t Student :
- Uji-t Student satu sampel – digunakan untuk menguji hipotesis tentang nilai mean sampel.
- Uji t Student untuk dua sampel independen : memungkinkan Anda menguji hipotesis tentang perbedaan antara rata-rata dua sampel independen.
- Uji-t Student untuk dua sampel berpasangan (atau sampel terkait) – digunakan untuk menyelidiki hipotesis tentang rata-rata sampel yang diuji dua kali.
Contoh uji t Student
Uji hipotesis untuk mean sampel adalah pengujian yang hipotesis nolnya dan pengujian hipotesis alternatifnya menyatakan sesuatu tentang nilai mean populasi.
Rumus uji t Student satu sampel adalah sebagai berikut:

Emas:
-

adalah statistik uji hipotesis untuk mean, yang ditentukan oleh distribusi t Student.
-

adalah sarana sampel.
-

adalah nilai mean yang diajukan dalam uji hipotesis.
-

adalah deviasi standar sampel.
-

adalah ukuran sampel.
Setelah nilai uji t Student dihitung, maka hasil uji statistik dengan nilai kritis harus diinterpretasikan untuk menolak atau tidak hipotesis nol:
- Jika uji hipotesis mean adalah dua sisi, hipotesis nol ditolak jika nilai absolut uji t Student lebih besar dari nilai kritis t α/2|n-1 .
- Jika uji hipotesis untuk mean cocok dengan ekor kanan, hipotesis nol ditolak jika nilai uji-t Student lebih besar dari nilai kritis t α|n-1 .
- Jika uji hipotesis untuk mean cocok dengan ekor kiri, hipotesis nol ditolak jika nilai uji-t Student lebih kecil dari nilai kritis -t α|n-1 .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
Perhatikan bahwa nilai uji kritis diperoleh dari tabel distribusi Student.
Uji t Student untuk sampel independen
Uji-t Student untuk sampel independen digunakan untuk menolak atau menerima hipotesis adanya hubungan antara mean dua populasi, misalnya mean dua populasi berbeda atau mean populasi A lebih besar dari rata-rata. . populasiB.
Namun dalam hal ini rumus uji-t Student bervariasi tergantung pada apakah varians populasi dapat diasumsikan sama atau tidak. Kami kemudian akan melihat dua kemungkinan kasus.
Penyimpangan yang tidak diketahui dan sama
Rumus perhitungan uji t Student untuk sampel independen ketika varians populasi tidak diketahui tetapi diasumsikan sama adalah sebagai berikut:

Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan mean dengan varians yang tidak diketahui, yang mengikuti distribusi t Student dengan derajat kebebasan n 1 + n 2 -2.
-

adalah rata-rata populasi 1.
-

adalah rata-rata populasi 2.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah deviasi standar gabungan.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Simpangan baku gabungan kedua sampel dihitung menggunakan rumus berikut:

Variasi yang tidak diketahui dan berbeda
Jika varians populasi tidak diketahui dan diasumsikan berbeda, maka rumus menghitung uji t Student untuk sampel independen adalah sebagai berikut:

Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan mean dengan varians yang tidak diketahui, yang mengikuti distribusi t Student.
-

adalah rata-rata populasi 1.
-

adalah rata-rata populasi 2.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah simpangan baku populasi 1.
-

adalah simpangan baku populasi 2.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Namun dalam hal ini derajat kebebasan distribusi t Student dihitung dengan menggunakan rumus berikut:

Uji t siswa untuk sampel berpasangan atau terkait
Tes ini digunakan apabila dua sampel yang diteliti saling berkaitan satu sama lain, sehingga sebenarnya merupakan satu sampel individu yang telah dianalisis dua kali (setiap kali dalam kondisi berbeda).
Misalnya, Anda dapat menganalisis nilai siswa dalam mata pelajaran matematika dan statistik untuk melihat apakah terdapat perbedaan yang signifikan antara rata-rata kedua mata pelajaran tersebut. Dalam hal ini, nilai matematika setiap siswa dihubungkan dengan nilai statistik siswa yang sama.
Rumus uji-t Student untuk sampel berpasangan atau berhubungan adalah:
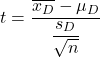
Emas:
-

adalah statistik pengujian hipotesis untuk mean berpasangan, yang ditentukan oleh distribusi t Student.
-
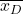
adalah mean sampel yang dibentuk oleh perbedaan data.
-
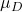
adalah nilai mean yang diajukan dalam uji hipotesis.
-
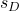
adalah simpangan baku sampel yang dibentuk oleh perbedaan data.
-

adalah ukuran sampel.
Asumsi uji-t Student
Untuk melakukan uji t Student, syarat-syarat berikut harus dipenuhi:
- Kontinuitas – Data sampel bersifat kontinu.
- Keacakan : Sampel data dipilih secara acak.
- Homogenitas : Varians data sampel bersifat homogen.
- Normalitas – Distribusi yang menentukan sampel data mendekati normal.
Bagaimana melakukan uji t Student
Terakhir, secara ringkas, langkah-langkah yang harus diikuti untuk melakukan uji t Student dirinci.
- Tentukan hipotesis nol dan hipotesis alternatif dari pengujian hipotesis.
- Tetapkan tingkat signifikansi (α) uji hipotesis.
- Verifikasi bahwa asumsi uji t Student terpenuhi.
- Terapkan rumus uji-t Student yang sesuai dan hitung statistik pengujiannya.
- Interpretasikan hasil uji t Student dengan membandingkannya dengan nilai kritis tes.