Cara melakukan tes tukey di r
ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.
Jika nilai p keseluruhan tabel ANOVA berada di bawah tingkat signifikansi tertentu, maka kita memiliki cukup bukti untuk mengatakan bahwa setidaknya salah satu mean kelompok berbeda dari mean kelompok lainnya.
Namun, hal ini tidak memberi tahu kita kelompok mana yang berbeda satu sama lain. Hal ini menunjukkan kepada kita bahwa tidak semua rata-rata kelompok adalah sama. Untuk mengetahui secara pasti kelompok mana yang berbeda satu sama lain, kita perlu melakukan tes post hoc .
Salah satu tes post hoc yang paling umum digunakan adalah tes Tukey , yang memungkinkan kita melakukan perbandingan berpasangan antara rata-rata setiap kelompok sambil mengendalikan tingkat kesalahan berdasarkan kelompok .
Tutorial ini menjelaskan cara melakukan tes Tukey di R.
Catatan: Jika salah satu kelompok dalam penelitian Anda dianggap sebagai kelompok kontrol, Anda sebaiknya menggunakan uji Dunnett sebagai uji post-hoc.
Contoh: Tes Tukey di R
Langkah 1: Pasangkan model ANOVA.
Kode berikut menunjukkan cara membuat kumpulan data palsu dengan tiga kelompok (A, B, dan C) dan menyesuaikan model ANOVA satu arah ke data untuk menentukan apakah nilai rata-rata setiap kelompok sama:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Kita dapat melihat bahwa p-value keseluruhan dari tabel ANOVA adalah 7.55e-11 . Karena angka ini kurang dari 0,05, kami mempunyai cukup bukti untuk mengatakan bahwa nilai rata-rata pada setiap kelompok tidak sama. Jadi, kita dapat melakukan uji Tukey untuk mengetahui secara pasti mean kelompok mana yang berbeda.
Langkah 2: Lakukan tes Tukey.
Kode berikut menunjukkan cara menggunakan fungsi TukeyHSD() untuk melakukan pengujian Tukey:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
Nilai p menunjukkan ada atau tidaknya perbedaan yang signifikan secara statistik antara masing-masing program. Hasilnya menunjukkan bahwa terdapat perbedaan yang signifikan secara statistik antara rata-rata penurunan berat badan setiap program pada tingkat signifikansi 0,05.
Khususnya:
- Nilai P selisih mean antara B dan A: 0,0100545
- Nilai P untuk selisih mean antara C dan A: 0,0000000
- Nilai P untuk selisih mean antara C dan B: 0,0000199
Langkah 3: Visualisasikan hasilnya.
Kita juga dapat menggunakan fungsi plot(TukeyHSD()) untuk memvisualisasikan interval kepercayaan:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
Catatan: Argumen las menetapkan bahwa label centang harus tegak lurus (las=2) terhadap sumbu.
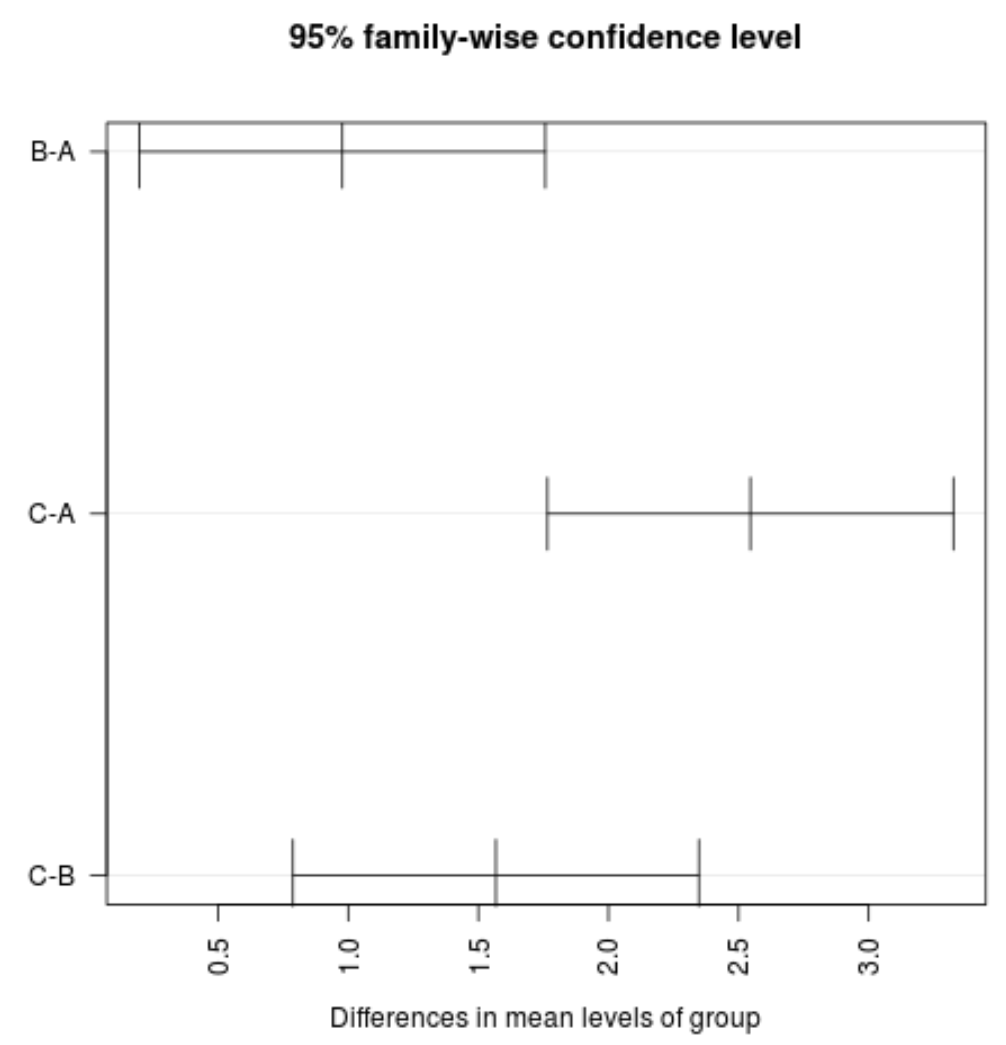
Kita dapat melihat bahwa tidak ada interval kepercayaan untuk nilai rata-rata antar kelompok yang mengandung nilai nol, yang menunjukkan bahwa terdapat perbedaan yang signifikan secara statistik dalam rata-rata kerugian antara ketiga kelompok. Hal ini konsisten dengan semua nilai p untuk pengujian hipotesis kami yang kurang dari 0,05.
Untuk contoh khusus ini, kita dapat menyimpulkan sebagai berikut:
- Nilai rata-rata kelompok C jauh lebih tinggi dibandingkan nilai rata-rata kelompok A dan B.
- Nilai rata-rata kelompok B jauh lebih tinggi dibandingkan nilai rata-rata kelompok A.
Sumber daya tambahan
Panduan Menggunakan Pengujian Post-Hoc dengan ANOVA
Bagaimana melakukan ANOVA satu arah di R
Cara melakukan ANOVA dua arah di R