Pengantar singkat tentang validasi silang tinggalkan satu keluar (loocv)

Untuk mengevaluasi performa suatu model pada kumpulan data, kita perlu mengukur seberapa cocok prediksi yang dibuat oleh model tersebut dengan data yang diamati.

Cara paling umum untuk mengukurnya adalah dengan menggunakan mean square error (MSE), yang dihitung sebagai berikut:

MSE = (1/n)*Σ(y _saya – f(x _saya )) ²

Emas:

• n: jumlah total observasi
• y _i : Nilai respon observasi ^ke-i
• f(x _i ) : Nilai respon prediksi observasi ^ke -i

Semakin dekat prediksi model dengan observasi, maka MSE akan semakin rendah.

Dalam praktiknya, kami menggunakan proses berikut untuk menghitung MSE model tertentu:

1. Bagilah kumpulan data menjadi kumpulan pelatihan dan kumpulan pengujian.

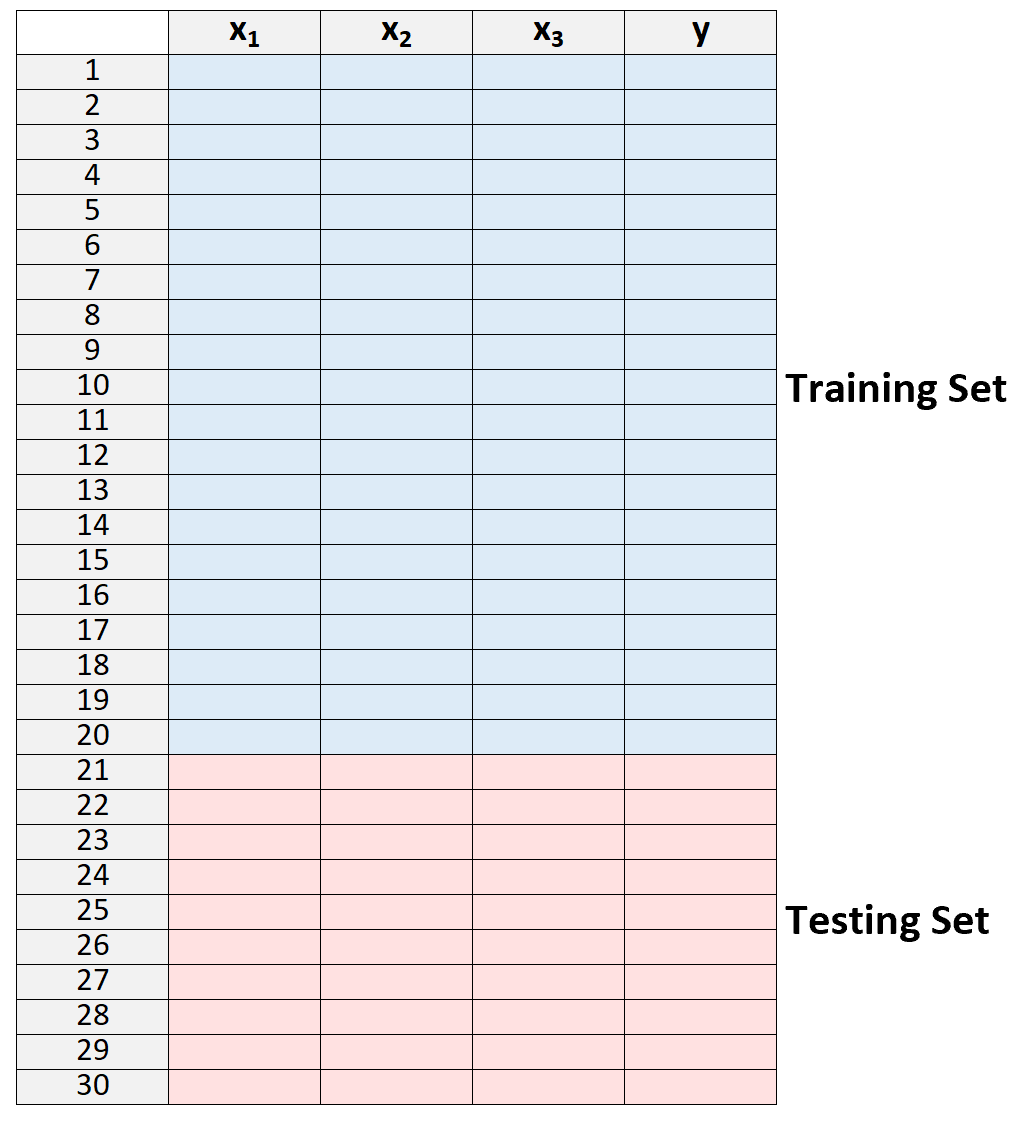
2. Buat model hanya dengan menggunakan data dari set pelatihan.

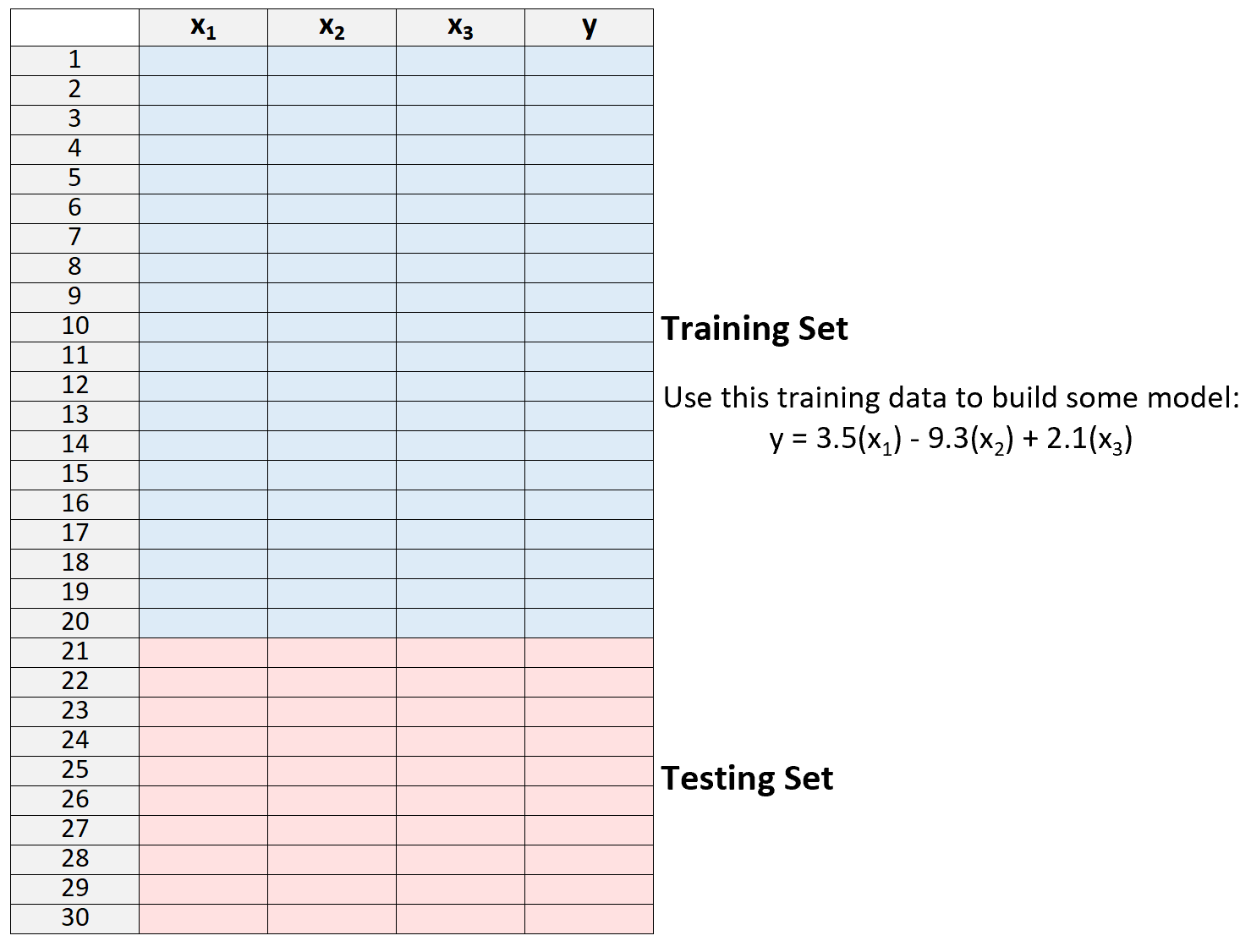
3. Gunakan model untuk membuat prediksi tentang set pengujian dan mengukur MSE – ini disebut MSE pengujian .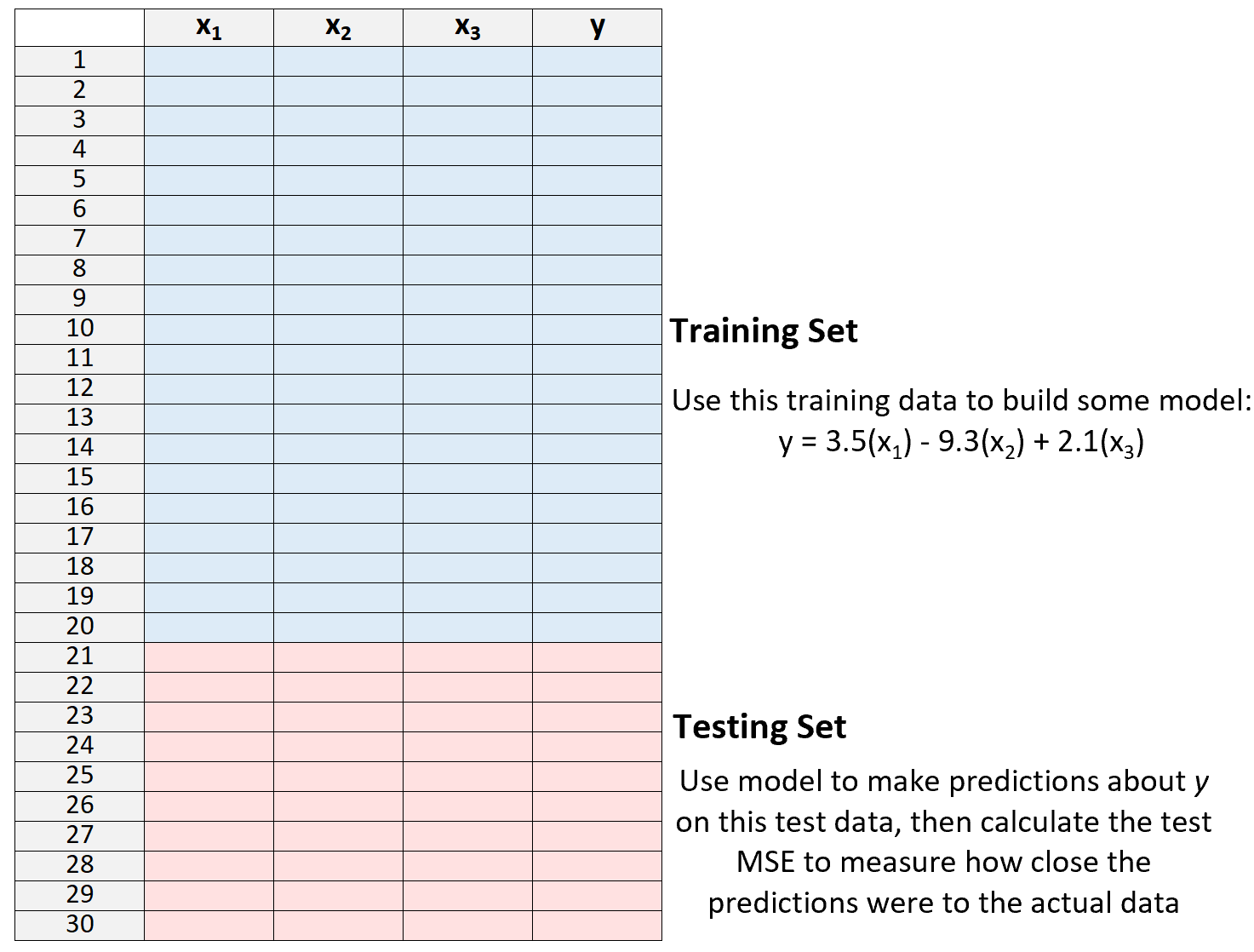

Pengujian MSE memberi kita gambaran tentang seberapa baik kinerja suatu model pada data yang belum pernah dilihat sebelumnya, yaitu data yang belum pernah digunakan untuk “melatih” model tersebut.

Namun, kelemahan menggunakan satu set tes adalah tes MSE dapat bervariasi secara signifikan tergantung pada observasi yang digunakan dalam set pelatihan dan tes.

Ada kemungkinan bahwa jika kita menggunakan kumpulan observasi yang berbeda untuk set pelatihan dan set pengujian, MSE pengujian kita bisa menjadi jauh lebih besar atau lebih kecil.

Salah satu cara untuk menghindari masalah ini adalah dengan menyesuaikan model beberapa kali menggunakan set pelatihan dan pengujian yang berbeda setiap kali, lalu menghitung UMK pengujian sebagai rata-rata dari semua UMK pengujian.

Metode umum ini dikenal sebagai validasi silang dan bentuk spesifiknya dikenal sebagai validasi silang Tinggalkan Satu Keluar .

Validasi Silang Tinggalkan Satu Keluar

Validasi silang tanpa keluar menggunakan pendekatan berikut untuk mengevaluasi model:

1. Pisahkan kumpulan data menjadi kumpulan pelatihan dan kumpulan pengujian, dengan menggunakan semua kecuali satu observasi sebagai bagian dari kumpulan pelatihan:

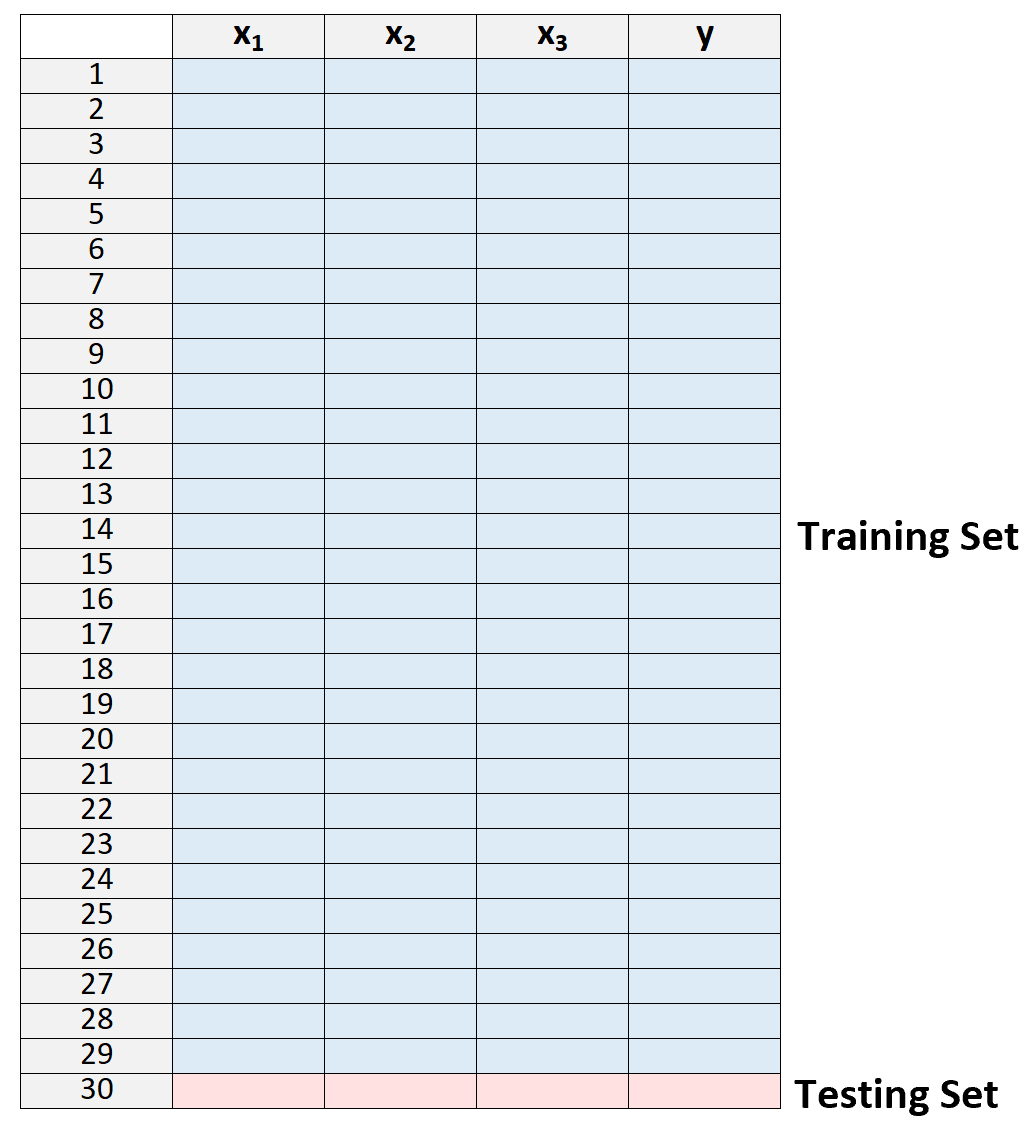
Perhatikan bahwa kami hanya menyisakan satu observasi “di luar” set pelatihan. Di sinilah metode ini mendapat nama validasi silang “leave-one-out”.

2. Buat model hanya dengan menggunakan data dari set pelatihan.

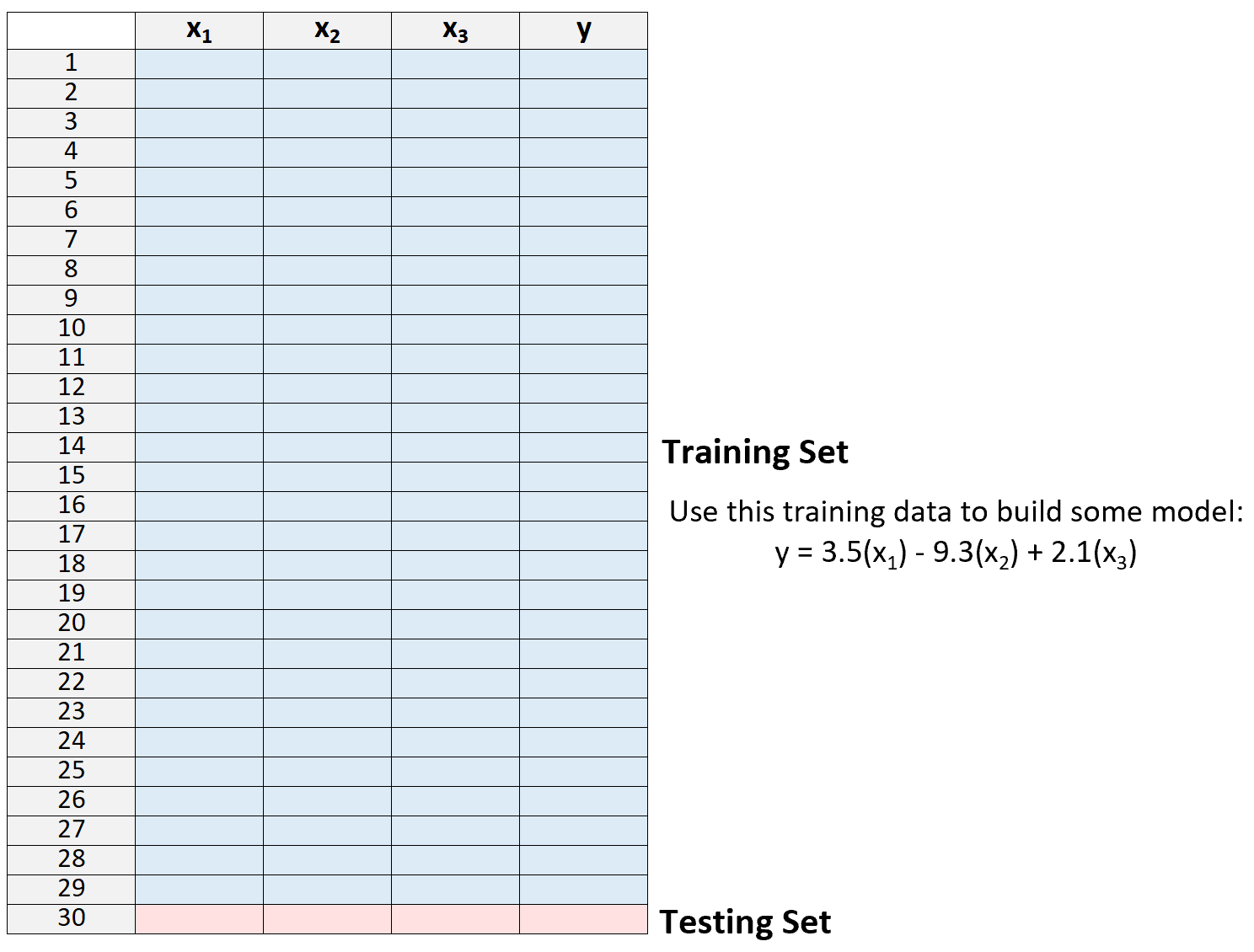
3. Gunakan model untuk memprediksi nilai respons dari observasi tunggal yang dikecualikan dari model dan menghitung MSE.

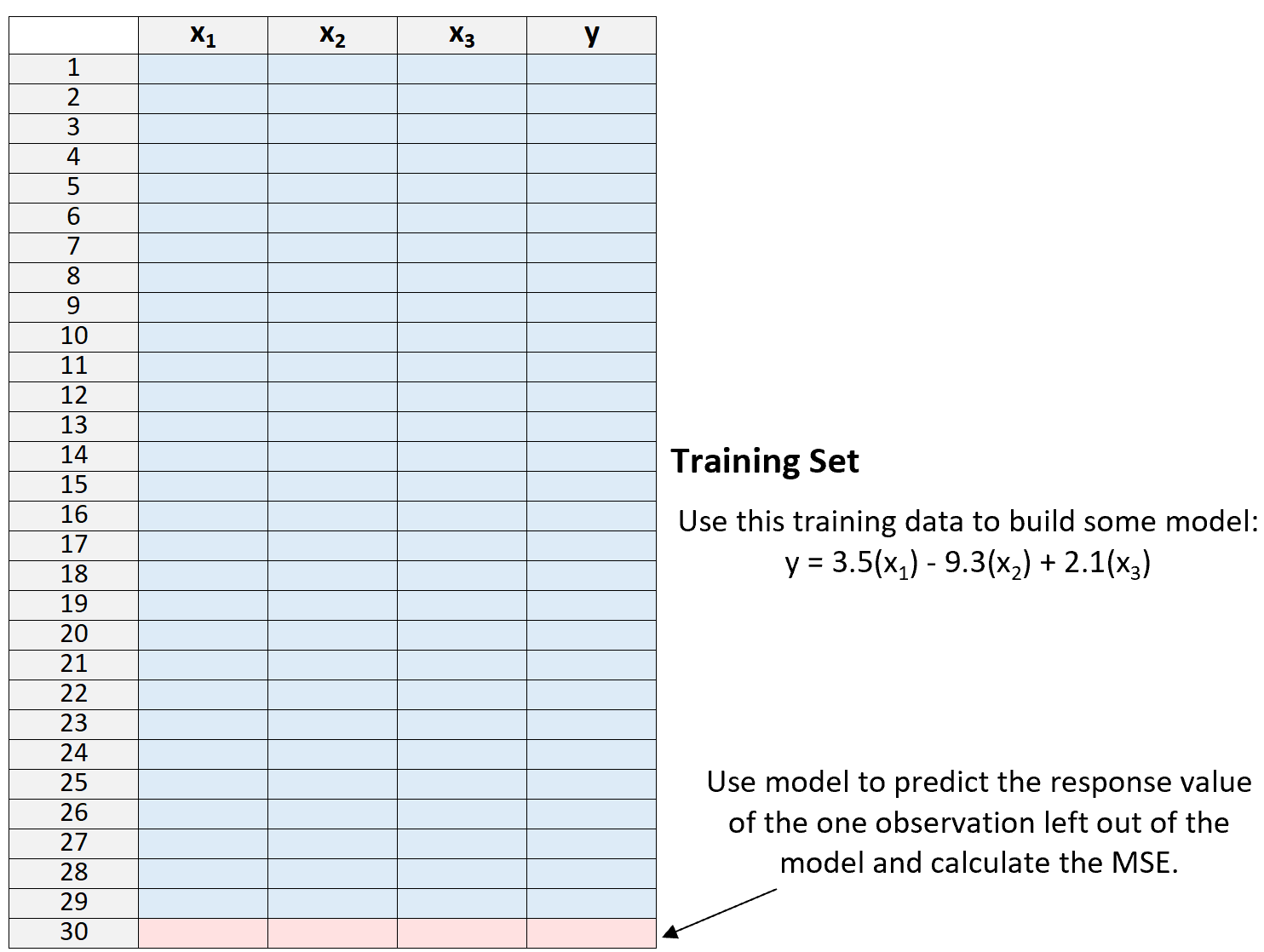
4. Ulangi proses tersebut sebanyak n kali.

Terakhir, kami mengulangi proses ini sebanyak n kali (di mana n adalah jumlah total observasi dalam kumpulan data), sehingga menyisakan observasi yang berbeda dari kumpulan pelatihan setiap kali.

Kami kemudian menghitung UMK pengujian sebagai rata-rata dari semua UMK pengujian:

Uji MSE = (1/n)*ΣMSE _i

Emas:

• n: jumlah total observasi dalam kumpulan data
• MSEi: tes MSE selama periode pemasangan model ^ke-i .

Kelebihan dan Kekurangan LOOCV

Validasi silang cuti-satu-keluar memberikan keuntungan sebagai berikut:

• Hal ini memberikan ukuran pengujian MSE yang jauh lebih tidak bias dibandingkan dengan menggunakan satu set pengujian, karena kami berulang kali menyesuaikan model ke kumpulan data yang berisi n-1 observasi.
• Hal ini cenderung tidak melebih-lebihkan MSE tes dibandingkan dengan menggunakan satu set tes.

Namun, validasi silang secara langsung mempunyai kelemahan sebagai berikut:

• Menggunakan proses ini bisa memakan waktu lama jika n besar.
• Hal ini juga dapat memakan waktu jika suatu model sangat kompleks dan membutuhkan waktu lama untuk menyesuaikan dengan kumpulan data.
• Ini bisa memakan biaya komputasi yang mahal.

Untungnya, komputasi modern telah menjadi sangat efisien di sebagian besar wilayah sehingga LOOCV menjadi metode yang jauh lebih masuk akal untuk digunakan dibandingkan beberapa tahun yang lalu.

Perhatikan bahwa LOOCV juga dapat digunakan dalam konteks regresi dan klasifikasi . Untuk masalah regresi, uji MSE dihitung sebagai akar rata-rata kuadrat selisih antara prediksi dan observasi, sedangkan untuk masalah klasifikasi, uji MSE dihitung sebagai persentase observasi yang diklasifikasikan dengan benar selama n penyesuaian model yang berulang.

Cara menjalankan LOOCV di R & Python

Tutorial berikut memberikan contoh langkah demi langkah tentang cara menjalankan LOOCV untuk model tertentu dalam R dan Python:

Validasi Silang Tinggalkan Satu Keluar di R
Validasi Silang Tinggalkan Satu Keluar dengan Python