Apa yang dimaksud dengan tingkat beta dalam statistik? (definisi & #038; contoh)

Dalam statistik, kami menggunakan pengujian hipotesis untuk menentukan apakah hipotesis tentang suatu parameter populasi benar.

Uji hipotesis selalu memiliki dua hipotesis berikut:

Hipotesis nol (H ₀ ): Data sampel konsisten dengan keyakinan dominan mengenai parameter populasi.

Hipotesis Alternatif ( _HA ): Data sampel menunjukkan bahwa hipotesis yang dinyatakan dalam hipotesis nol tidak benar. Dengan kata lain, penyebab non-acak mempengaruhi data.

Setiap kali kita melakukan uji hipotesis, selalu ada empat kemungkinan hasil:

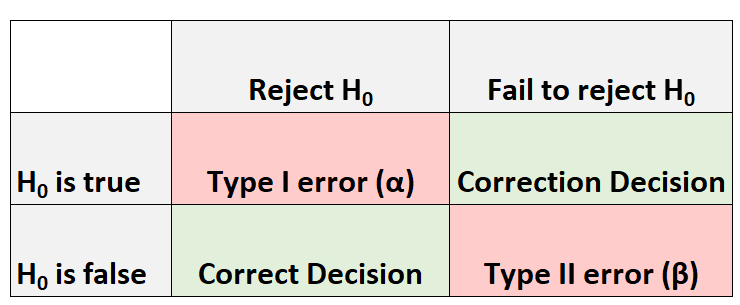
Ada dua jenis kesalahan yang bisa kita lakukan:

• Kesalahan tipe I: Kita menolak hipotesis nol padahal hipotesis tersebut benar. Probabilitas melakukan jenis kesalahan ini dilambangkan dengan α .
• Kesalahan tipe II: Kita gagal menolak hipotesis nol padahal hipotesis tersebut salah. Kemungkinan melakukan jenis kesalahan ini dicatat β .

Hubungan antara alfa dan beta

Idealnya, peneliti ingin probabilitas terjadinya kesalahan Tipe I dan probabilitas terjadinya kesalahan Tipe II menjadi rendah.

Namun, ada kompromi antara kedua kemungkinan ini. Jika kita menurunkan tingkat alfa, kita dapat mengurangi kemungkinan menolak hipotesis nol padahal hipotesis tersebut benar, namun hal ini justru meningkatkan tingkat beta – kemungkinan kita gagal menolak hipotesis nol padahal hipotesis itu salah.

Hubungan antara kekuatan dan beta

Kekuatan uji hipotesis mengacu pada kemungkinan mendeteksi suatu efek atau perbedaan ketika suatu efek atau perbedaan benar-benar ada. Dengan kata lain, ini adalah probabilitas menolak hipotesis nol yang salah dengan benar.

Ini dihitung sebagai berikut:

Daya = 1 – β

Pada umumnya peneliti menginginkan kekuatan suatu tes yang tinggi sehingga jika terdapat pengaruh atau perbedaan maka tes tersebut dapat mendeteksinya.

Dari persamaan di atas, kita dapat melihat bahwa cara terbaik untuk meningkatkan kekuatan suatu pengujian adalah dengan mengurangi level beta. Dan cara terbaik untuk mengurangi tingkat beta biasanya dengan meningkatkan ukuran sampel.

Contoh berikut menunjukkan cara menghitung tingkat beta uji hipotesis dan menunjukkan mengapa meningkatkan ukuran sampel dapat mengurangi tingkat beta.

Contoh 1: Hitung Beta untuk Uji Hipotesis

Misalkan seorang peneliti ingin menguji apakah berat rata-rata widget yang diproduksi di sebuah pabrik kurang dari 500 ons. Kita tahu bahwa deviasi standar bobot adalah 24 ons dan peneliti memutuskan untuk mengumpulkan sampel acak sebanyak 40 widget.

Hipotesis berikut akan terwujud pada α = 0,05:

• H ₀ : µ = 500
• _HA : μ < 500

Sekarang bayangkan berat rata-rata widget yang dihasilkan sebenarnya adalah 490 ons. Dengan kata lain, hipotesis nol harus ditolak.

Kita dapat menggunakan langkah-langkah berikut untuk menghitung tingkat beta – probabilitas tidak menolak hipotesis nol padahal hipotesis tersebut sebenarnya ditolak:

Langkah 1: Temukan wilayah tanpa penolakan.

Menurut kalkulator nilai kritis Z, nilai kritis kiri pada α = 0,05 adalah -1,645 .

Langkah 2: Temukan sampel minimum yang gagal kami tolak.

Statistik uji dihitung sebagai z = ( x – μ) / (s/ √n )

Jadi, kita dapat menyelesaikan persamaan ini untuk mean sampel:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/ √40 )
• x = 493.758

Langkah 3: Tentukan probabilitas bahwa rata-rata sampel minimum akan benar-benar terjadi.

Kita dapat menghitung probabilitas ini sebagai berikut:

• P(Z ≥ (493.758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Menurut kalkulator CDF normal , peluang Z ≥ 0,99 adalah 0,1611 .

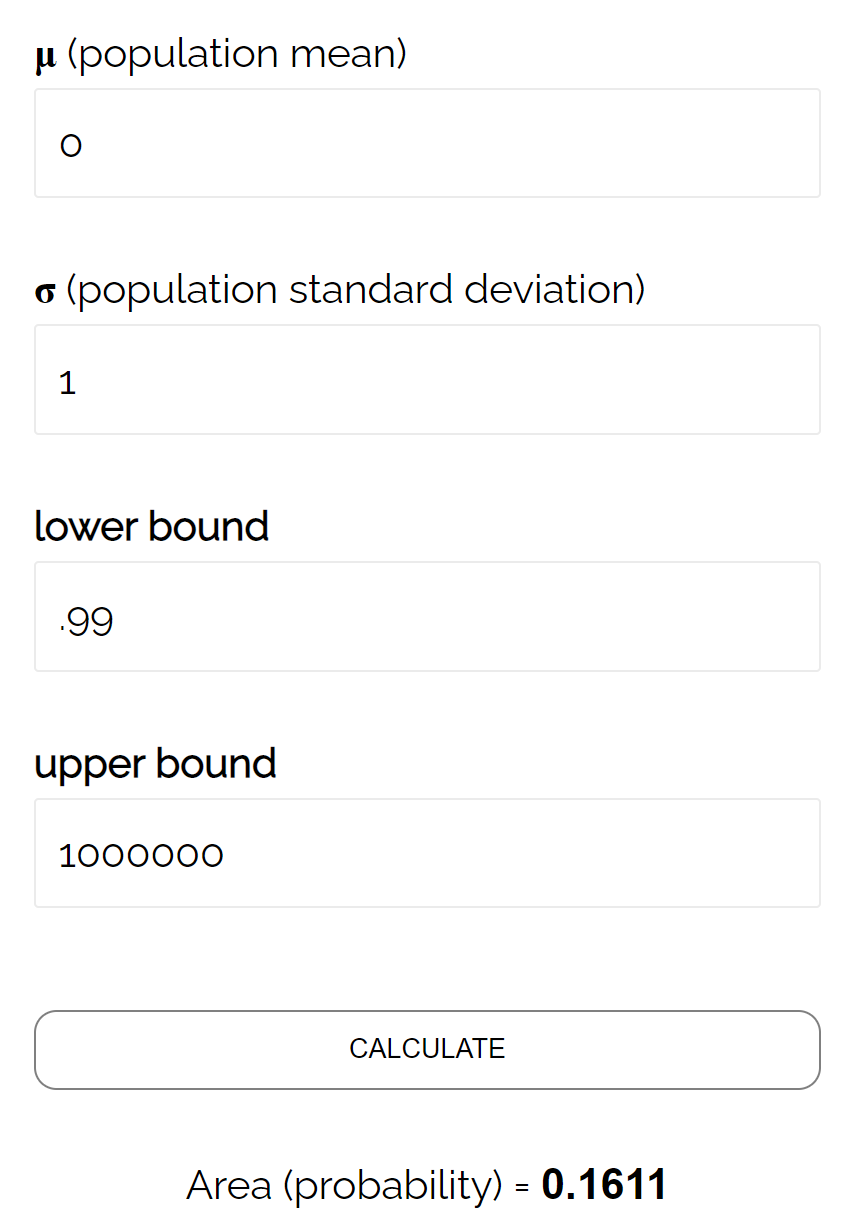
Jadi, level beta untuk pengujian ini adalah β = 0,1611. Artinya ada kemungkinan 16,11% tidak terdeteksi perbedaannya jika rata-rata sebenarnya adalah 490 ons.

Contoh 2: Hitung Beta untuk Pengujian dengan Ukuran Sampel Lebih Besar

Sekarang misalkan peneliti melakukan uji hipotesis yang sama persis, namun menggunakan sampel n = 100 widget. Kita dapat mengulangi tiga langkah yang sama untuk menghitung level beta untuk pengujian ini:

Langkah 1: Temukan wilayah tanpa penolakan.

Menurut kalkulator nilai kritis Z, nilai kritis kiri pada α = 0,05 adalah -1,645 .

Langkah 2: Temukan sampel minimum yang gagal kami tolak.

Statistik uji dihitung sebagai z = ( x – μ) / (s/ √n )

Jadi, kita dapat menyelesaikan persamaan ini untuk mean sampel:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/√ 100 )
• x = 496,05

Langkah 3: Tentukan probabilitas bahwa rata-rata sampel minimum akan benar-benar terjadi.

Kita dapat menghitung probabilitas ini sebagai berikut:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Menurut kalkulator CDF normal , peluang Z ≥ 2,52 adalah 0,0059.

Jadi, tingkat beta untuk pengujian ini adalah β = 0,0059. Artinya, hanya ada kemungkinan 0,59% untuk tidak mendeteksi perbedaannya jika rata-rata sebenarnya adalah 490 ons.

Perhatikan bahwa hanya dengan meningkatkan ukuran sampel dari 40 menjadi 100, peneliti dapat mengurangi tingkat beta dari 0,1611 menjadi 0,0059.

Bonus: Gunakan kalkulator kesalahan Tipe II ini untuk menghitung level beta suatu pengujian secara otomatis.

Sumber daya tambahan

Pengantar Pengujian Hipotesis
Cara Menulis Hipotesis Nol (5 Contoh)
Penjelasan tentang nilai P dan signifikansi statistik