Mengetik

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa yang dimaksud dengan mengkarakterisasi distribusi dalam statistik. Dengan demikian, Anda akan menemukan definisi tipifikasi, contoh tipifikasi suatu variabel dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.

Apa itu mengetik?

Dalam statistik, normalisasi adalah proses di mana transformasi linier diterapkan pada suatu distribusi sehingga mean dan deviasi standarnya masing-masing sama dengan nol dan satu.

Lebih tepatnya, pengetikan melibatkan pengurangan mean dari variabel acak dan kemudian membaginya dengan deviasi standar.

Pengetikan juga bisa disebut normalisasi atau standardisasi.

Rumus masukan

Untuk mengklasifikasikan suatu variabel, Anda harus mengurangkan meannya lalu membaginya dengan deviasi standarnya. Oleh karena itu, rumus untuk memasukkan variabel adalah sebagai berikut:

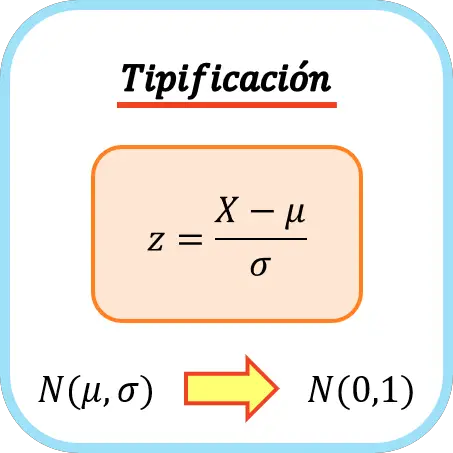
Emas

$\mu$

adalah mean dari variabel tersebut

$X$

Dan

$\sigma$

deviasi standarnya (atau deviasi standar).

Oleh karena itu, entri sebenarnya adalah perubahan variabel, karena transformasi linier diterapkan pada variabel tersebut.

Contoh entri

Mengingat pengertian tipifikasi dan rumusnya, berikut adalah contoh konkrit untuk memahami konsep tersebut secara utuh.

Suatu variabel acak kontinu mengikuti distribusi normal dengan mean 45 dan standar deviasi 10, berapakah peluang memperoleh nilai kurang dari atau sama dengan 60?

$N(45,10)$

Untuk mencari peluang berdistribusi normal kita perlu menggunakan tabel karakteristiknya, namun untuk melakukannya kita perlu melakukan proses pengetikan terlebih dahulu. Jadi kita kurangi meannya dan bagi dengan deviasi standar ke nilai probabilitas:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Setelah kita melakukan standarisasi, kita beralih ke tabel probabilitas distribusi normal untuk melihat probabilitas apa yang sesuai dengan nilai 1,5:

Seperti dapat dilihat pada tabel tipifikasi distribusi normal, nilai yang dihitung pada langkah sebelumnya sesuai dengan probabilitas berikut:

$\displaystyle P(Z\leq 1,5)=0,9332$

Oleh karena itu, probabilitas memperoleh nilai yang sama dengan atau kurang dari 60 adalah 93,32%.

Latihan Mengetik Terpecahkan

Hitung probabilitas distribusi normal berikut yang mean dan deviasi standarnya masing-masing 120 dan 50.

$N(120,50)$

Peluang memperoleh nilai kurang dari atau sama dengan 208.
Kemungkinan memperoleh nilai lebih besar dari 137.

Lihat solusinya

Di kedua bagian soal, kita perlu mengetikkan distribusi normal untuk menghitung probabilitas.

Kita mulai dengan menghitung probabilitas pengetikan nilai yang kurang dari atau setara dengan 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

Dan sekarang mari kita lihat tabel di atas, probabilitas apa yang sesuai dengan nilai 1,76:

$\displaystyle P(Z\leq 1,76)=0,9608$

Kedua, kita akan menghitung probabilitas memperoleh nilai yang lebih besar dari 137. Dengan cara yang sama, kita mulai dengan mengetikkan variabel:

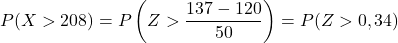$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ Namun, tabel terlampir hanya memiliki probabilitas kumulatif terendah, jadi untuk menggunakan tabel tersebut kita harus mengubah probabilitasnya terlebih dahulu:

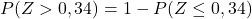$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ Dan terakhir, kami akan mencatat dari tabel terlampir probabilitas yang sesuai dengan nilai Z yang dihitung:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

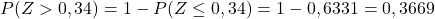
Apa gunanya mengetik?

Untuk lebih memahami pengertian tipifikasi, kita akan melihat kegunaannya dan kapan suatu variabel harus diketik.

Pada dasarnya, standardisasi digunakan untuk membandingkan nilai distribusi dengan mean dan varians yang berbeda. Demikian pula, standardisasi juga digunakan untuk menghitung probabilitas.

Dengan menstandarkan dua nilai distribusi yang mempunyai karakteristik berbeda, kita dapat melihat nilai mana yang lebih besar atau lebih kecil dibandingkan dengan keseluruhan distribusi. Atau dengan kata lain, dengan menerapkan proses tipifikasi, kita dapat melihat nilai mana yang paling dekat atau terjauh dari mean distribusinya.

Selain itu, seperti dijelaskan di atas, tipifikasi juga memungkinkan penghitungan probabilitas, karena umumnya tabel probabilitas didasarkan pada distribusi yang diketik.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya