Apa itu y hat dalam statistik?

Dalam statistik, istilah y hat (ditulis ŷ ) mengacu pada nilai taksiran suatu variabel respon dalam model regresi linier .

Kami biasanya menulis persamaan regresi yang diperkirakan sebagai berikut:

ŷ = β ₀ + β ₁ x

Emas:

• ŷ : Nilai estimasi variabel respon
• β ₀ : Nilai rata-rata variabel respon ketika variabel prediktor bernilai nol
• β ₁ : rata-rata perubahan variabel respon yang berhubungan dengan kenaikan satu satuan variabel prediktif

Misalnya, kita memiliki kumpulan data berikut yang menunjukkan jumlah jam belajar oleh enam siswa berbeda beserta nilai ujian akhir mereka:

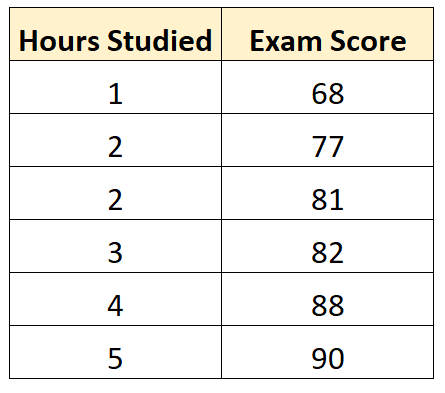
Misalkan kita menggunakan perangkat lunak statistik (seperti R , Excel , Python , atau bahkan secara manual) agar sesuai dengan model regresi berikut menggunakan jam belajar sebagai variabel prediktor dan memeriksa hasil sebagai variabel respons:

Skor = 66.615 + 5.0769*(Jam)

Cara menginterpretasikan koefisien regresi pada model ini adalah sebagai berikut:

• Nilai ujian rata-rata seorang siswa yang belajar nol jam adalah 66,615 .
• Nilai ujian meningkat rata-rata 5,0769 poin untuk setiap tambahan jam belajar.

Kita dapat menggunakan persamaan regresi ini untuk memperkirakan nilai siswa tertentu berdasarkan jumlah jam belajar.

Misalnya, seorang siswa yang belajar selama 3 jam harus mendapat nilai:

Skor = 66,615 + 5,0769*(3) = 81,85

Mengapa Y Hat digunakan?

Simbol “topi” dalam statistik digunakan untuk menunjukkan istilah “perkiraan”. Misalnya, ŷ digunakan untuk menunjukkan perkiraan variabel respons.

Biasanya, ketika kita menyesuaikan model regresi linier, kita menggunakan sampel data dari suatu populasi, karena ini lebih mudah dan memakan waktu lebih sedikit dibandingkan mengumpulkan data untuk setiap kemungkinan observasi dalam suatu populasi.

Jadi ketika kita menemukan persamaan regresi, kita hanya memperkirakan hubungan sebenarnya antara variabel prediktor dan variabel respon.

Inilah sebabnya kami menggunakan istilah ŷ dalam persamaan regresi, bukan y.

Sumber daya tambahan

Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Pengenalan variabel penjelas dan respon