4 contoh penggunaan uji chi-square dalam kehidupan nyata
Dalam statistik, ada dua jenis uji Chi-kuadrat:
1. Uji kesesuaian chi-kuadrat – Digunakan untuk menentukan apakah suatu variabel kategori mengikuti distribusi hipotetis atau tidak.
2. Uji Independensi Chi Square – Digunakan untuk mengetahui ada atau tidaknya hubungan yang signifikan antara dua variabel kategori.
Dalam artikel ini, kami membagikan beberapa contoh bagaimana masing-masing jenis uji Chi-kuadrat ini digunakan dalam situasi dunia nyata.
Contoh 1: Uji kesesuaian chi-kuadrat
Misalkan seorang pemilik toko mengklaim bahwa jumlah pelanggan yang datang ke tokonya sama setiap hari dalam seminggu.
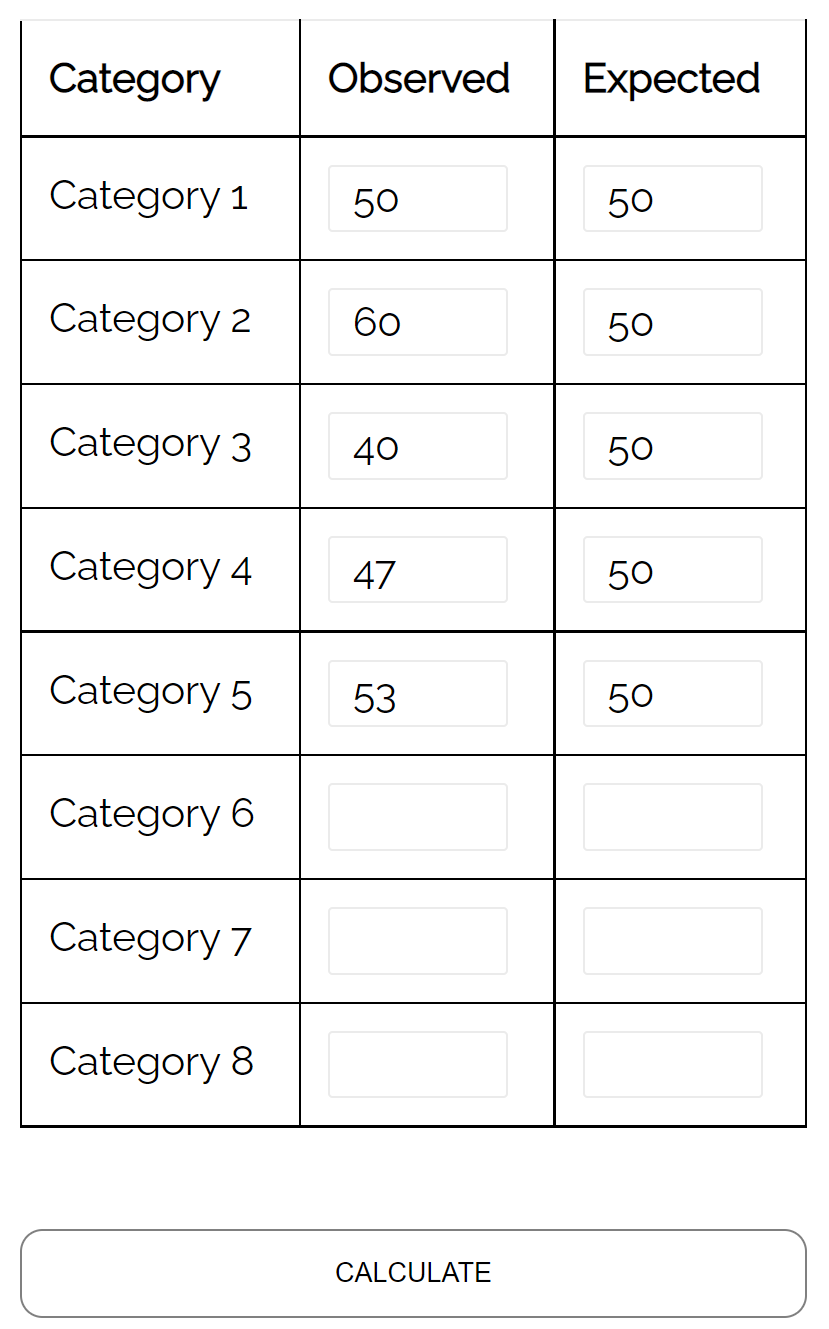
Untuk menguji hipotesis ini, dia mencatat jumlah pelanggan yang datang ke toko pada minggu tertentu dan menemukan hal berikut:
- Senin: 50 pelanggan
- Selasa: 60 pelanggan
- Rabu: 40 pelanggan
- Kamis: 47 pelanggan
- Jumat: 53 pelanggan
Dia dapat menggunakan uji kesesuaian chi-kuadrat untuk menentukan apakah distribusi pelanggan yang datang setiap hari konsisten dengan hipotesis distribusinya.
Dengan menggunakan kalkulator tes kesesuaian chi-kuadrat , dia dapat melihat bahwa nilai p dari tes tersebut adalah 0,359 .

Karena nilai p ini tidak kurang dari 0,05, tidak ada cukup bukti untuk menyatakan bahwa distribusi pelanggan sebenarnya berbeda dari yang diklaim oleh pemilik toko.
Contoh 2: Uji kesesuaian chi-kuadrat
Misalkan seorang ahli biologi menyatakan bahwa empat spesies rusa berbeda dalam jumlah yang sama memasuki kawasan hutan tertentu setiap minggunya.
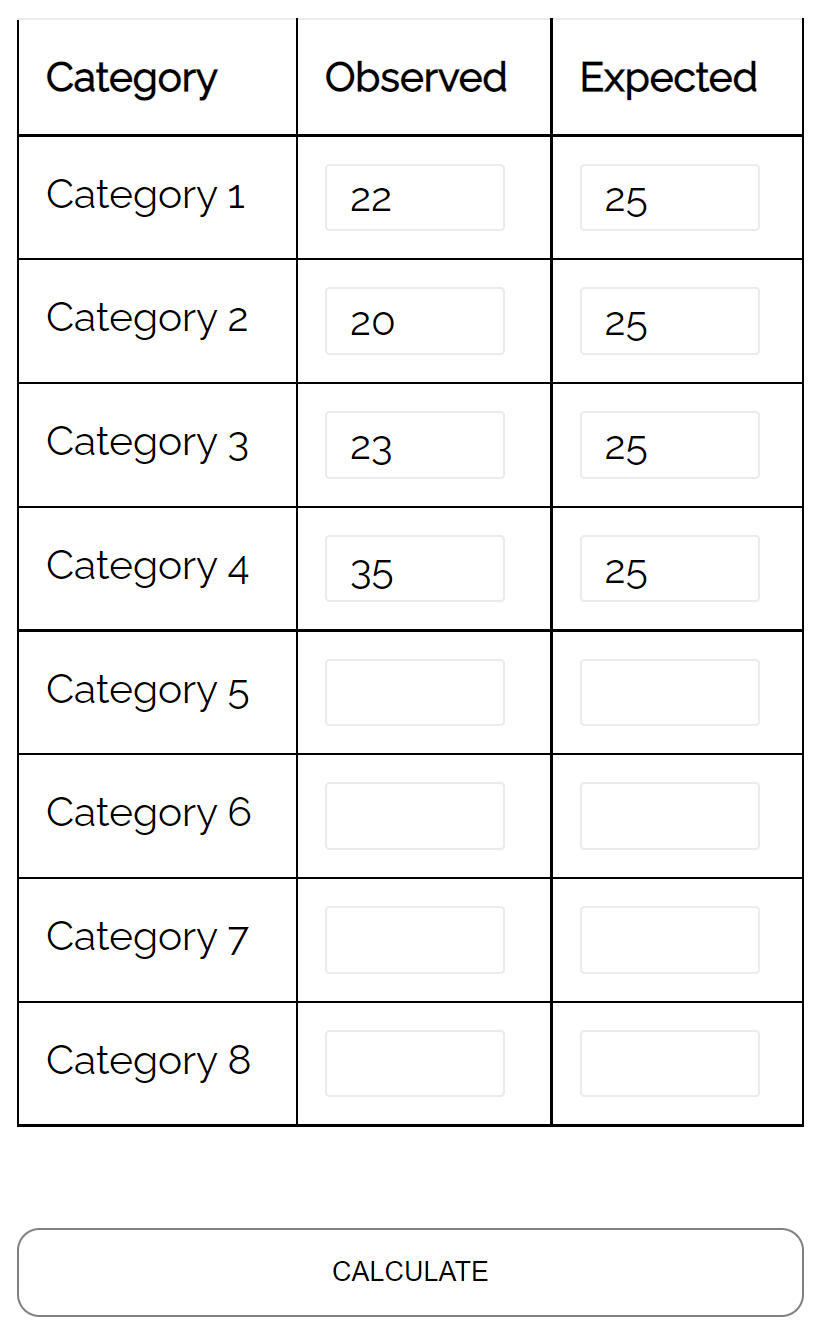
Untuk menguji hipotesis ini, dia mencatat jumlah setiap spesies rusa yang memasuki kawasan hutan selama seminggu:
- Spesies #1: 22
- Spesies #2: 20
- Spesies #3: 23
- Spesies #4: 35
Dia dapat menggunakan uji kesesuaian chi-kuadrat untuk menentukan apakah sebaran spesies rusa yang memasuki kawasan hutan setiap minggunya sesuai dengan sebaran hipotetisnya.
Dengan menggunakan kalkulator tes kesesuaian chi-kuadrat , dia dapat melihat bahwa nilai p untuk tes tersebut adalah 0,137 .
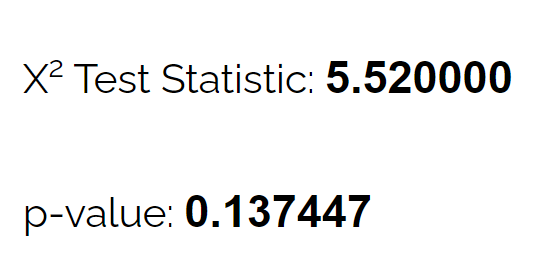
Karena nilai p ini tidak kurang dari 0,05, tidak ada cukup bukti untuk menyatakan bahwa sebaran rusa yang sebenarnya berbeda dari yang dinyatakan oleh para ahli biologi.
Contoh 3: Uji independensi chi-kuadrat
Misalkan seorang pembuat kebijakan di suatu kota ingin mengetahui apakah gender dikaitkan dengan preferensi suatu partai politik atau tidak.
Dia memutuskan untuk mengambil sampel acak sederhana dari 500 pemilih dan menanyakan preferensi partai politik mereka. Berikut tabel hasil surveinya:
| Republik | Demokrat | Mandiri | Total | |
| Pria | 120 | 90 | 40 | 250 |
| Perempuan | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Uji independensi chi-square dapat digunakan untuk menentukan apakah terdapat hubungan yang signifikan secara statistik antara kedua variabel.
Dengan menggunakan kalkulator tes independensi chi-kuadrat , dia dapat melihat bahwa nilai p dari tes tersebut adalah 0,649 .
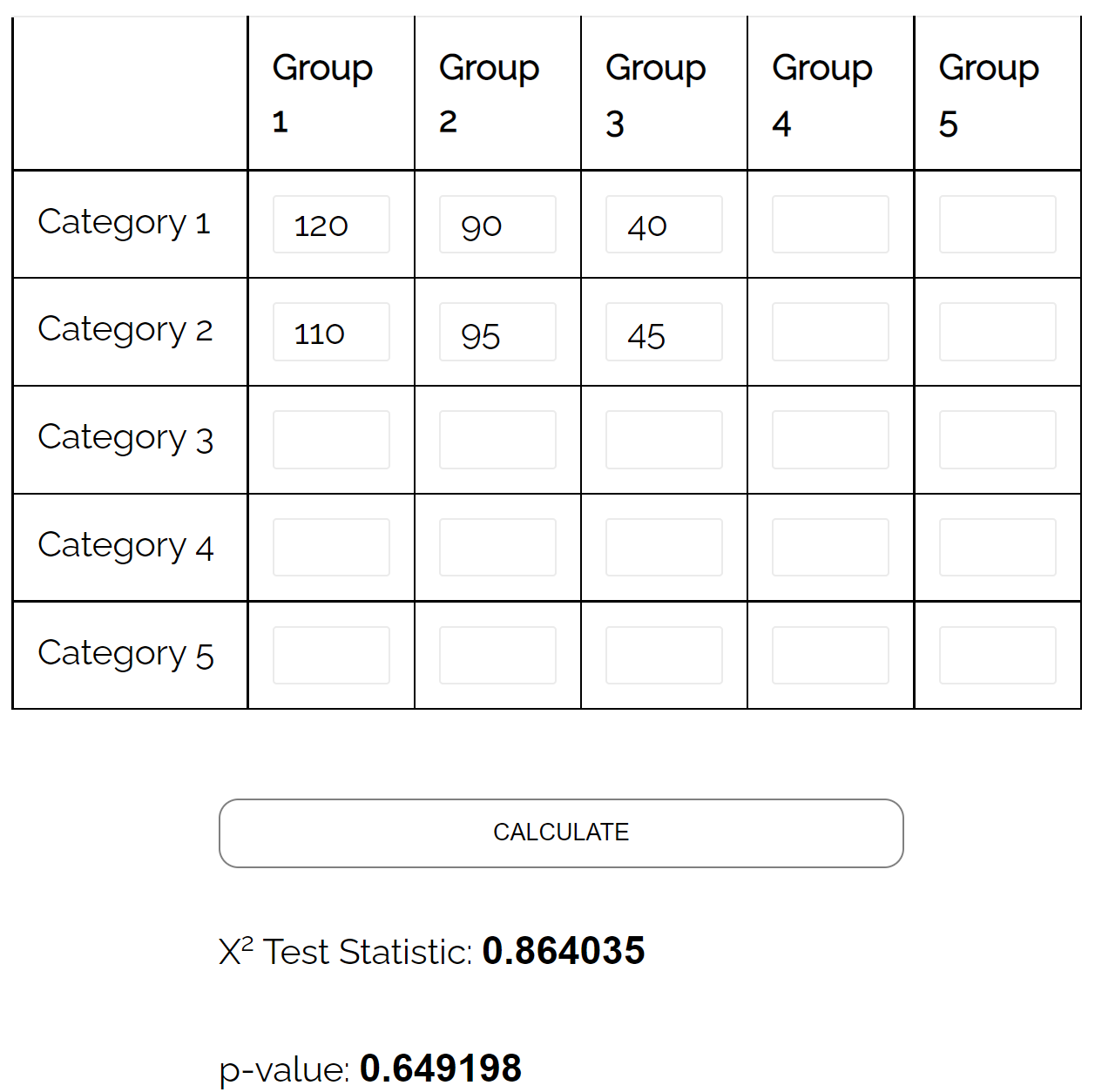
Karena nilai p tidak kurang dari 0,05, tidak terdapat cukup bukti untuk menyatakan adanya hubungan antara gender dan preferensi partai politik.
Contoh 4: Uji independensi chi-kuadrat
Misalkan seorang peneliti ingin mengetahui apakah status perkawinan dikaitkan dengan pencapaian pendidikan atau tidak.
Dia memutuskan untuk mengambil sampel acak sederhana sebanyak 300 individu dan memperoleh hasil sebagai berikut:
| Sekolah menengah atas | Sarjana | Master atau lebih tinggi | Total | |
| Telah menikah | 20 | 100 | 35 | 155 |
| Sarjana | 50 | 80 | 15 | 145 |
| Total | 70 | 180 | 50 | 300 |
Uji independensi chi-square dapat digunakan untuk menentukan apakah terdapat hubungan yang signifikan secara statistik antara kedua variabel.
Dengan menggunakan kalkulator tes independensi chi-kuadrat , dia dapat melihat bahwa nilai p dari tes tersebut adalah 0,000011 .
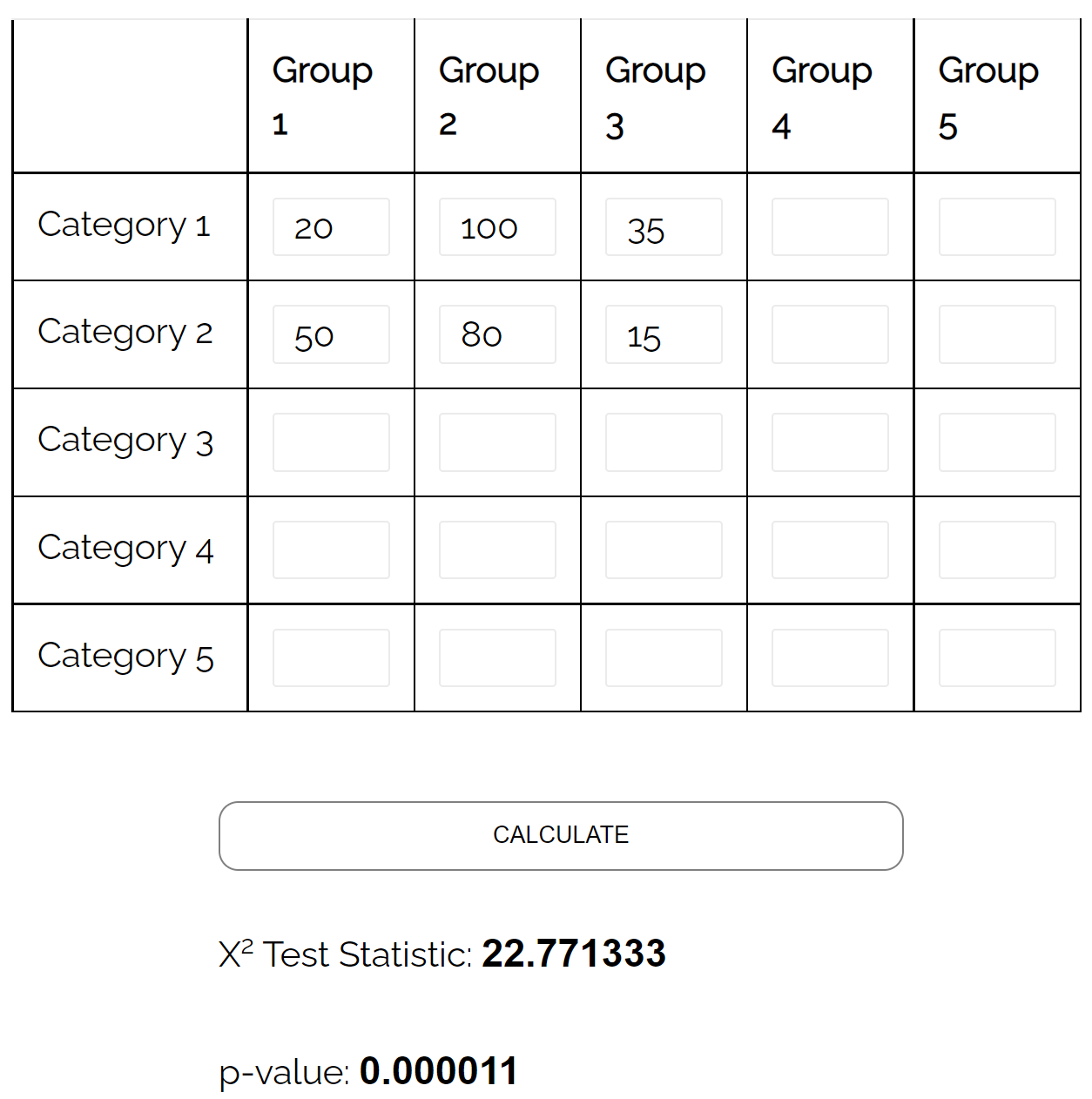
Karena nilai p kurang dari 0,05, terdapat cukup bukti yang menyatakan bahwa terdapat hubungan antara status perkawinan dan tingkat pendidikan.
Sumber daya tambahan
Tutorial berikut memberikan pengenalan berbagai jenis uji Chi-kuadrat:
Tutorial berikut menjelaskan perbedaan antara uji Chi-kuadrat dan uji statistik lainnya: