Cara melakukan uji independensi chi-kuadrat di sas
Uji independensi chi-square digunakan untuk mengetahui ada atau tidaknya hubungan yang signifikan antara dua variabel kategori .
Contoh berikut menunjukkan cara melakukan uji independensi chi-kuadrat di SAS.
Contoh: Uji independensi chi-kuadrat di SAS
Misalkan kita ingin mengetahui apakah gender dikaitkan dengan preferensi terhadap suatu partai politik atau tidak. Kami mengambil sampel acak sederhana dari 500 pemilih dan menanyakan preferensi partai politik mereka.
Berikut tabel hasil surveinya:
| Republik | Demokrat | Mandiri | Total | |
| Pria | 120 | 90 | 40 | 250 |
| Perempuan | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Gunakan langkah-langkah berikut untuk melakukan uji independensi chi-square di SAS untuk menentukan apakah gender dikaitkan dengan preferensi partai politik.
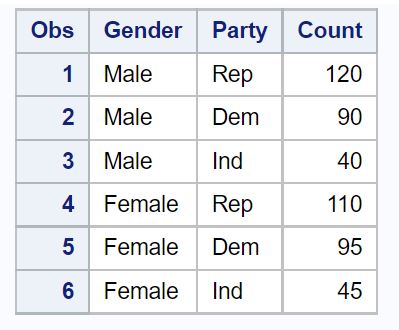
Langkah 1: Buat datanya.
Pertama, kita akan membuat kumpulan data di SAS untuk menampung respons survei:
/*create dataset*/ data my_data; input Gender$Party$Count; datalines ; Male Rep 120 Male Dem 90 Male Ind 40 Female Rep 110 Female Dem 95 Female Ind 45 ; run ; /*print dataset*/ proc print data =my_data;
Langkah 2: Lakukan uji independensi chi-kuadrat.
Kemudian kita dapat menggunakan kode berikut untuk melakukan uji independensi chi-kuadrat:
/*perform Chi-Square Test of Independence*/ proc freq data =my_data; Gender*Party / chisq tables ; weightCount ; run ;
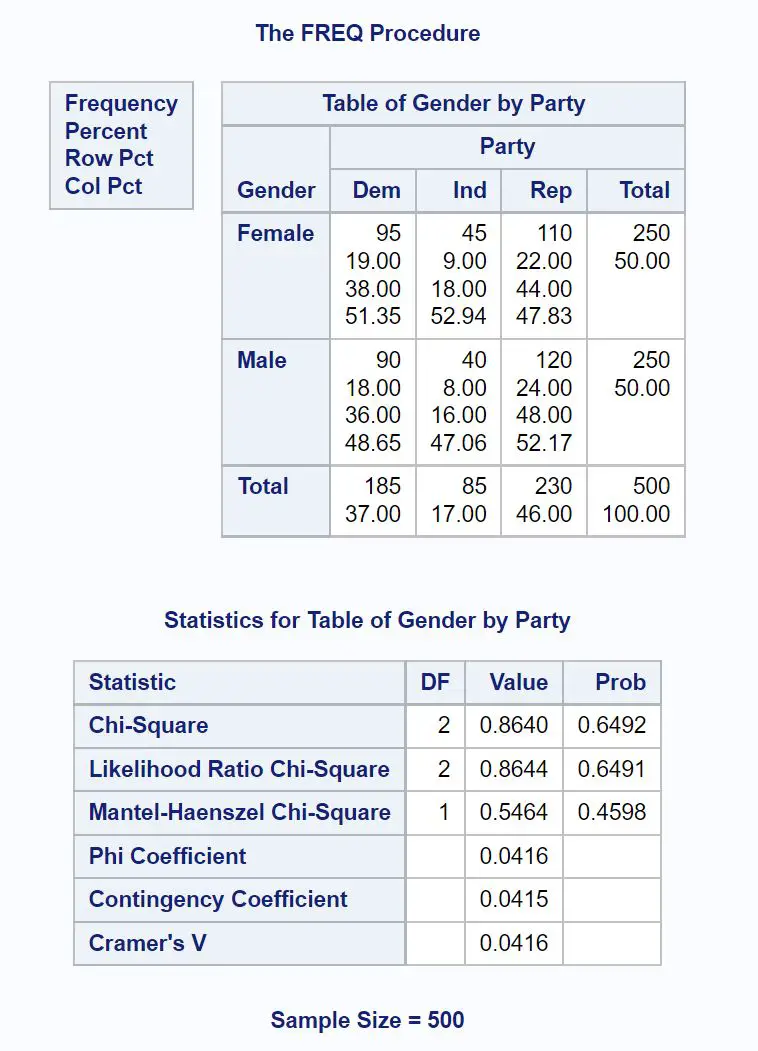
Ada dua nilai menarik dalam keluarannya:
- Statistik uji chi-kuadrat: 0,8640
- Nilai p yang sesuai: 0,6492
Ingatlah bahwa uji independensi chi-kuadrat menggunakan hipotesis nol dan hipotesis alternatif berikut:
- H 0 : Kedua variabel tersebut saling bebas.
- H A : Kedua variabel tersebut tidak independen.
Karena nilai p (0,6492) dari pengujian tersebut tidak kurang dari 0,05, kami gagal menolak hipotesis nol.
Artinya, kami tidak memiliki cukup bukti untuk menyatakan adanya hubungan antara gender dan preferensi partai politik.
Dengan kata lain, preferensi gender dan partai politik bersifat independen.
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang uji independensi chi-kuadrat:
Pengantar uji independensi chi-kuadrat
Kalkulator kemandirian uji chi-kuadrat
Cara Melakukan Tes Independensi Chi-Kuadrat di Excel