Cara melakukan uji kesesuaian chi kuadrat di spss

Uji kesesuaian chi-kuadrat digunakan untuk menentukan apakah suatu variabel kategori mengikuti distribusi hipotetis atau tidak.

Tutorial ini menjelaskan cara melakukan uji kesesuaian chi-kuadrat di SPSS.

Contoh: Uji kesesuaian chi-kuadrat di SPSS

Seorang pemilik toko mengatakan bahwa jumlah pelanggan yang datang ke tokonya sama setiap hari dalam seminggu. Untuk menguji hipotesis ini, peneliti mencatat jumlah pelanggan yang datang ke toko pada minggu tertentu dan menemukan hal berikut:

• Senin: 50 pelanggan
• Selasa: 60 pelanggan
• Rabu: 40 pelanggan
• Kamis: 47 pelanggan
• Jumat: 53 pelanggan

Gunakan langkah-langkah berikut untuk melakukan uji kesesuaian chi-kuadrat di SPSS untuk menentukan apakah data konsisten dengan klaim pemilik toko.

Langkah 1: Masukkan datanya.

Pertama, masukkan data ke dalam SPSS dengan format sebagai berikut:

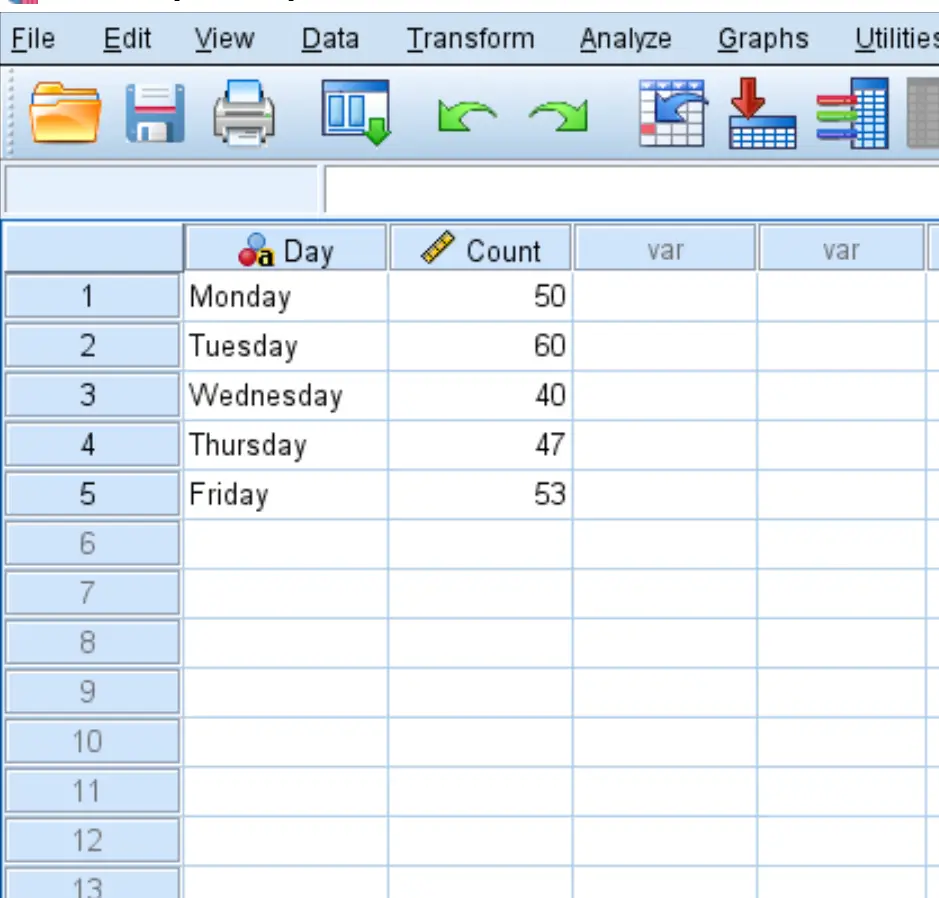
Langkah 2: Gunakan kotak berbobot.

Agar pengujian berfungsi dengan benar, kita perlu memberi tahu SPSS bahwa variabel “Hari” harus diberi bobot oleh variabel “Nomor”.

Klik tab Data , lalu klik Weight Cases :

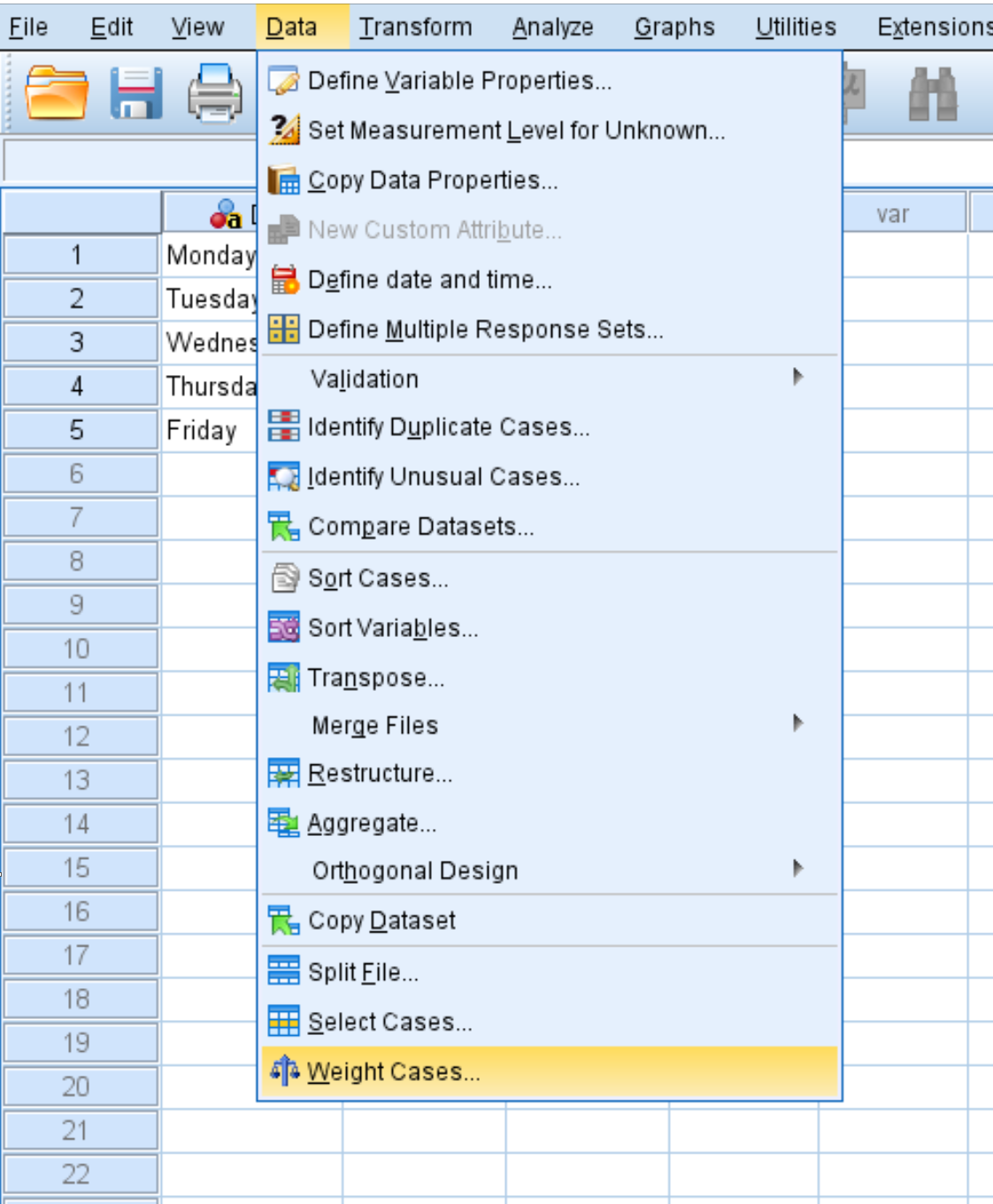
Di jendela baru yang muncul, seret variabel Hitung ke dalam area berlabel Daftar Variabel Uji. Lalu klik oke .

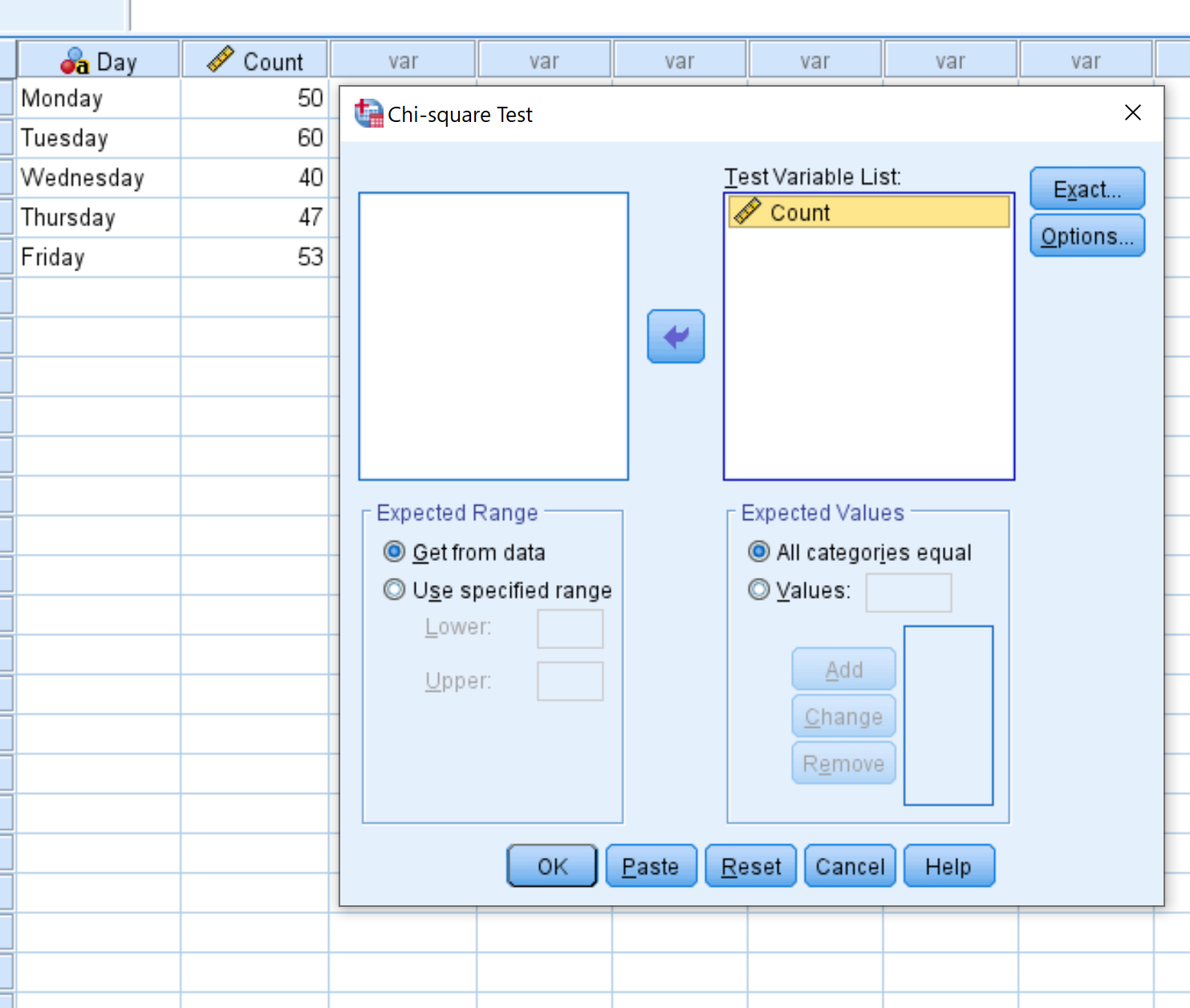
Langkah 3: Lakukan uji kecocokan chi-kuadrat.

Klik tab Analyze , lalu Nonparametric Tests , lalu Legacy Dialogs , lalu Chi Square :

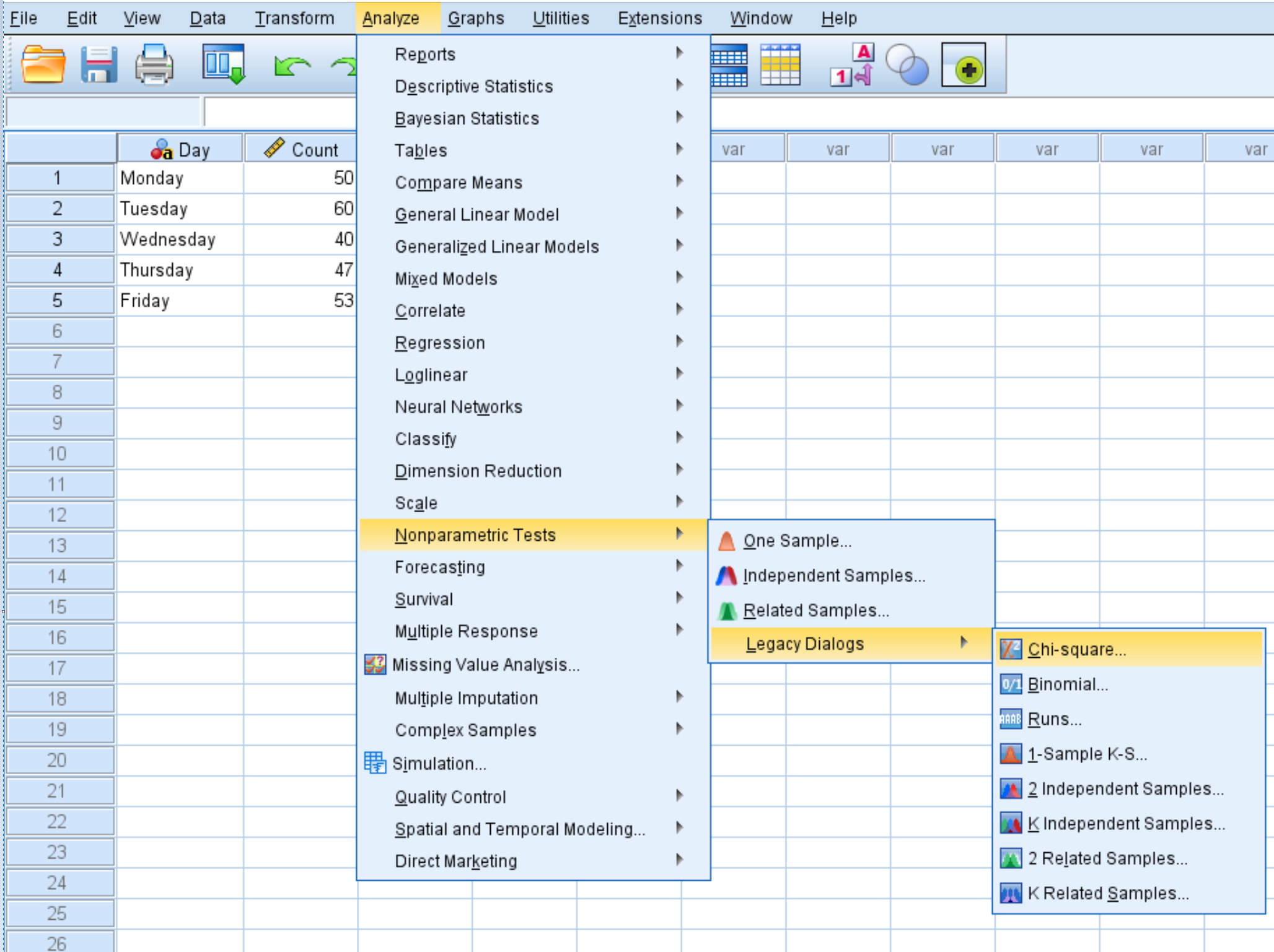
Di jendela baru yang muncul, seret variabel Hitung ke dalam area berlabel Daftar Variabel Uji.

Biarkan label dicentang di samping Semua kategori sama karena setiap kategori kami (yaitu hari dalam seminggu) memiliki jumlah pengunjung yang diharapkan sama setiap harinya. Lalu klik oke .

Langkah 4: Tafsirkan hasilnya .

Setelah Anda mengklik OK , akan muncul hasil tes kesesuaian chi-kuadrat:

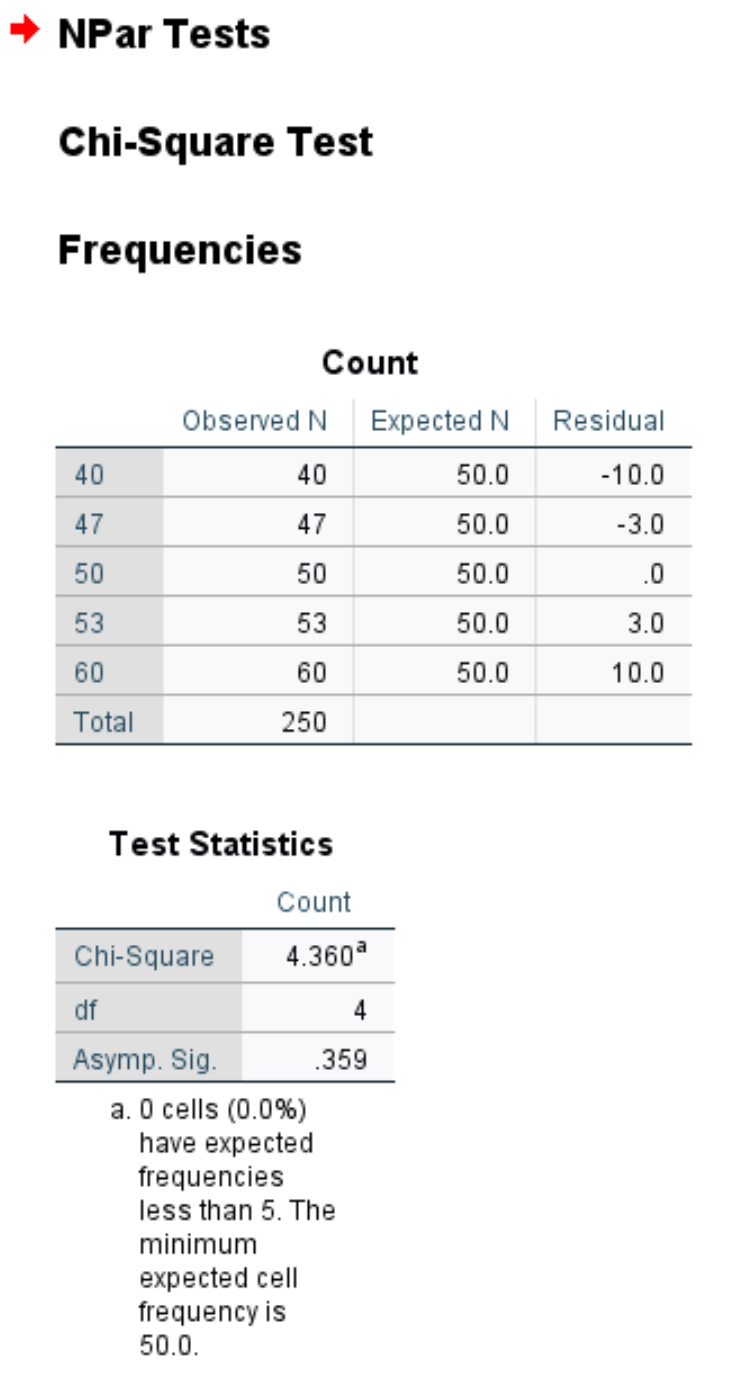
Tabel pertama menunjukkan jumlah pelanggan yang diamati dan diharapkan setiap hari dalam seminggu, serta sisa (yaitu perbedaan) antara yang diamati dan diharapkan.

Tabel kedua menampilkan angka-angka berikut:

Chi-square : Statistik uji chi-square yaitu 4,36.

df: Derajat kebebasan, dihitung sebagai #kategori-1 = 5-1 = 4.

Asymp. Sig: Nilai p yang sesuai dengan nilai Chi-kuadrat sebesar 4,36 dengan 4 derajat kebebasan, yaitu 0,359. Nilai ini juga dapat ditemukan dengan menggunakan kalkulator skor chi-kuadrat ke nilai-P.

Karena nilai p (0,359) tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Artinya, kami tidak mempunyai cukup bukti untuk mengatakan bahwa sebaran pelanggan sebenarnya berbeda dengan yang dilaporkan oleh pemilik toko.