Pengujian hipotesis untuk mean
Artikel ini menjelaskan apa yang dimaksud dengan pengujian hipotesis untuk mean dalam statistik. Dengan demikian, Anda akan menemukan rumus uji hipotesis untuk rata-rata dan, sebagai tambahan, latihan yang diselesaikan langkah demi langkah.
Apa yang dimaksud dengan pengujian hipotesis?
Pengujian hipotesis mean merupakan metode statistik yang digunakan untuk menolak atau menolak hipotesis nol suatu mean populasi.
Lebih khusus lagi, pengujian hipotesis untuk mean melibatkan penghitungan statistik uji dan membandingkannya dengan nilai kritis untuk menolak hipotesis nol atau tidak.
Perlu dicatat bahwa uji hipotesis memiliki nama yang berbeda; dalam statistik, mereka juga disebut kontras hipotesis, uji hipotesis, atau uji signifikansi.
Rumus Pengujian Hipotesis Mean
Selanjutnya kita akan melihat bagaimana statistik uji hipotesis untuk mean dihitung. Namun, rumusnya sedikit berbeda tergantung apakah variansnya diketahui atau tidak, jadi pertama-tama kita akan melihat cara melakukannya ketika varians diketahui dan kemudian ketika varians tidak diketahui.
Dengan penyimpangan yang diketahui
Rumus pengujian hipotesis untuk mean dengan varians yang diketahui adalah:

Emas:
-

adalah statistik uji hipotesis untuk mean.
-

adalah sarana sampel.
-

adalah nilai rata-rata yang diusulkan.
-

adalah simpangan baku populasi.
-

adalah ukuran sampel.
Setelah statistik uji hipotesis untuk mean dihitung, hasilnya harus diinterpretasikan untuk menolak atau menolak hipotesis nol:
- Jika uji hipotesis mean adalah dua sisi, hipotesis nol ditolak jika nilai absolut statistik lebih besar dari nilai kritis Z α/2 .
- Jika uji hipotesis untuk mean cocok dengan ekor kanan, hipotesis nol ditolak jika statistik lebih besar dari nilai kritis Z α .
- Jika uji hipotesis untuk mean cocok dengan ekor kiri, hipotesis nol ditolak jika statistiknya kurang dari nilai kritis -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
Dalam hal ini, nilai kritis diperoleh dari tabel distribusi normal terstandar .
Dengan varian yang tidak diketahui
Rumus pengujian hipotesis untuk mean yang variansinya tidak diketahui adalah:

Emas:
-

adalah statistik pengujian hipotesis untuk mean, yang ditentukan oleh distribusi t Student .
-

adalah sarana sampel.
-

adalah nilai rata-rata yang diusulkan.
-

adalah deviasi standar sampel.
-

adalah ukuran sampel.
Seperti sebelumnya, hasil perhitungan statistik uji harus diinterpretasikan dengan nilai kritis untuk menolak atau tidak hipotesis nol:
- Jika uji hipotesis mean adalah dua sisi, hipotesis nol ditolak jika nilai absolut statistik lebih besar dari nilai kritis t α/2|n-1 .
- Jika uji hipotesis untuk mean cocok dengan ekor kanan, hipotesis nol ditolak jika statistik lebih besar dari nilai kritis t α|n-1 .
- Jika uji hipotesis untuk mean cocok dengan ekor kiri, hipotesis nol ditolak jika statistiknya kurang dari nilai kritis -t α|n-1 .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
Apabila variansinya tidak diketahui maka nilai uji kritis diperoleh dari tabel distribusi Student.
Contoh Pengujian Hipotesis Mean di Dunia Nyata
Untuk memahami sepenuhnya konsep pengujian hipotesis untuk mean populasi, Anda dapat melihat contoh nyata dari jenis pengujian hipotesis ini di bawah.
- Sebuah perusahaan teknologi mengklaim baterai laptop yang dijualnya mampu bertahan hingga 6 jam. Kita memeriksa apakah hipotesis ini salah dengan melakukan uji hipotesis dengan tingkat signifikansi α = 0,05. Untuk melakukan ini, diputuskan untuk membeli 20 unit dan mengamati masa pakai baterai setiap komputer (nilai dinyatakan dalam jam):
5.2 5.9 7.1 4.2 6.5
8,5 4,6 6,8 6,9 5,8
5.1 6.5 7.0 5.3 6.2
5.7 6.6 7.5 5.1 6.1
Dalam hal ini, hipotesis nol dan hipotesis alternatif dari uji hipotesis tentang mean adalah sebagai berikut:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
Untuk menentukan statistik uji, pertama-tama kita perlu menghitung mean sampel dan deviasi standar sampel:
![]()
Karena varians populasi tidak diketahui, untuk mendapatkan statistik uji kita perlu menerapkan rumus pengujian hipotesis untuk mean dengan varians yang tidak diketahui:

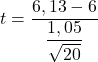
![]()
Sekarang kita perlu mencari nilai kritis uji hipotesis, jadi kita lihat tabel distribusi t Student untuk nilai yang sesuai. Derajat kebebasan t Student kurang satu dari ukuran sampel (20-1=19) dan, sebaliknya, probabilitas yang bersesuaian adalah setengah tingkat signifikansi (0,05/2= 0,025) karena ini adalah dua sisi pengujian hipotesis.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
Kesimpulannya, karena ini adalah uji hipotesis dua sisi dan nilai absolut statistik uji lebih kecil dari nilai kritis, maka hipotesis nol tidak ditolak, namun hipotesis alternatif ditolak.
![]()
Pengujian hipotesis untuk perbedaan rata-rata
Uji hipotesis perbedaan mean digunakan untuk menolak atau menerima hipotesis nol yang menyatakan mean dua populasi adalah sama.
Jadi hipotesis nol dari uji hipotesis untuk selisih dua mean selalu sebagai berikut:
![]()
Sedangkan hipotesis alternatifnya dapat berupa salah satu dari tiga hal berikut:
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
Maka rumus untuk menghitung statistik uji hipotesis selisih mean ketika varians diketahui adalah:
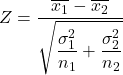
Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan dua mean dengan varians yang diketahui, yang mengikuti distribusi normal standar.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah varian populasi 1.
-

adalah varians populasi 2.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Sedangkan rumus menghitung statistik uji hipotesis selisih mean ketika varians tidak diketahui adalah sebagai berikut:
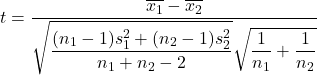
Emas:
-

adalah statistik pengujian hipotesis untuk selisih dua mean yang variansnya tidak diketahui, yang mengikuti distribusi t Student.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah varians sampel 1.
-

adalah varians sampel 2.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.