Pengujian hipotesis untuk perbedaan rata-rata
Artikel ini menjelaskan apa perbedaan mean pengujian hipotesis dalam statistik dan kegunaannya. Demikian pula, Anda akan menemukan cara melakukan uji hipotesis tentang perbedaan sarana dan latihan penyelesaian langkah demi langkah.
Apa yang dimaksud dengan pengujian hipotesis untuk perbedaan rata-rata?
Pengujian hipotesis perbedaan mean adalah uji statistik yang digunakan untuk menolak atau menerima hipotesis bahwa mean dua populasi berbeda. Artinya, uji hipotesis perbedaan mean digunakan untuk mengetahui apakah mean dua populasi sama atau berbeda.
Ingatlah bahwa keputusan yang diambil dalam pengujian hipotesis didasarkan pada tingkat kepercayaan yang telah ditetapkan sebelumnya, sehingga seseorang tidak dapat menjamin bahwa hasil pengujian hipotesis selalu benar, namun hasil yang paling mungkin benar adalah hasil tersebut.
Pengujian hipotesis untuk selisih dua mean melibatkan penghitungan statistik uji dan membandingkannya dengan nilai kritis untuk menolak hipotesis nol atau tidak. Di bawah ini kita akan melihat bagaimana melakukan uji hipotesis untuk perbedaan mean.
Terakhir, ingatlah bahwa dalam statistik, pengujian hipotesis juga dapat disebut kontras hipotesis, pengujian hipotesis, atau pengujian signifikansi.
Rumus Pengujian Hipotesis Perbedaan Rata-rata
Rumus yang harus digunakan untuk menguji hipotesis tentang perbedaan rata-rata bervariasi tergantung pada apakah varians populasi diketahui dan, jika tidak, apakah varian tersebut dapat diasumsikan sama atau berbeda. Jadi, di bagian ini, kita akan melihat rumus mana yang digunakan tergantung kasusnya.
Variasi yang diketahui
Rumus untuk menghitung statistik uji hipotesis selisih mean apabila varians diketahui adalah sebagai berikut:

Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan dua mean dengan varians yang diketahui, yang mengikuti distribusi normal standar.
-

adalah rata-rata populasi 1.
-

adalah rata-rata populasi 2.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah simpangan baku populasi 1.
-

adalah simpangan baku populasi 2.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Ingatlah bahwa ini adalah kasus yang paling jarang terjadi, jadi rumus ini hanya digunakan dalam beberapa kasus tertentu.
Penyimpangan yang tidak diketahui dan sama
Rumus untuk menghitung statistik uji hipotesis selisih mean ketika varians populasi tidak diketahui tetapi diasumsikan sama adalah:

Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan mean dengan varians yang tidak diketahui, yang mengikuti distribusi t Student dengan derajat kebebasan n 1 + n 2 -2.
-

adalah rata-rata populasi 1.
-

adalah rata-rata populasi 2.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah deviasi standar gabungan.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Simpangan baku gabungan kedua sampel dihitung dengan rumus berikut:

Variasi yang tidak diketahui dan berbeda
Jika varians populasi tidak diketahui dan diasumsikan berbeda, maka rumus menghitung statistik uji hipotesis untuk selisih mean adalah sebagai berikut:

Emas:
-

adalah statistik pengujian hipotesis untuk perbedaan mean dengan varians yang tidak diketahui, yang mengikuti distribusi t Student.
-

adalah rata-rata populasi 1.
-

adalah rata-rata populasi 2.
-

adalah rata-rata sampel 1.
-

adalah rata-rata sampel 2.
-

adalah simpangan baku populasi 1.
-

adalah simpangan baku populasi 2.
-

adalah ukuran sampel 1.
-

adalah ukuran sampel 2.
Namun dalam hal ini derajat kebebasan distribusi t Student dihitung dengan menggunakan rumus berikut:

Contoh nyata pengujian hipotesis untuk perbedaan mean
Untuk menyelesaikan asimilasi konsep pengujian hipotesis tentang perbedaan mean, kita akan melihat contoh konkrit dari jenis pengujian hipotesis ini.
- Anda ingin melakukan studi statistik terhadap gaji dua perusahaan pesaing, lebih khusus lagi Anda ingin mengetahui apakah rata-rata gaji kedua perusahaan tersebut berbeda. Untuk melakukan hal ini, diambil sampel sebanyak 47 pekerja dari satu perusahaan dan sampel lainnya sebanyak 55 pekerja dari perusahaan lain. Gaji rata-rata sebesar $40.000 dan deviasi standar sebesar $12.000 diperoleh dari sampel pertama, sedangkan gaji rata-rata sebesar $46.000 dan deviasi standar sebesar $18.000 diperoleh dari sampel kedua. Lakukan uji hipotesis dengan tingkat signifikansi 5% untuk mengetahui apakah rata-rata gaji berbeda atau tidak.
Dalam hal ini hipotesis nol dan hipotesis alternatif uji hipotesis selisih dua mean adalah sebagai berikut:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
Dalam hal ini, kesenjangan populasi tidak diketahui, namun dapat diasumsikan bahwa kesenjangan tersebut setara karena mereka adalah perusahaan pesaing dan kondisi kerja di pasar tempat mereka beroperasi sangat mirip. Oleh karena itu, rumus statistik pengujian hipotesis selisih mean yang sebaiknya digunakan adalah:

Oleh karena itu kami menghitung simpangan baku gabungan dari dua sampel:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
Kami sekarang menerapkan rumus pengujian hipotesis untuk perbedaan rata-rata:
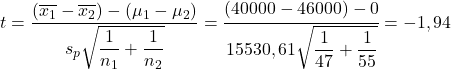
Di sisi lain, kita mencari nilai kritis uji hipotesis untuk perbedaan mean pada tabel t Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
Kemudian, karena nilai absolut statistik uji lebih kecil dari nilai uji kritis, maka hipotesis nol diterima dan hipotesis alternatif ditolak.
![]()