Cara melakukan uji kesesuaian chi kuadrat di excel

Uji kesesuaian chi-kuadrat digunakan untuk menentukan apakah suatu variabel kategori mengikuti distribusi hipotetis atau tidak.

Tutorial ini menjelaskan cara melakukan uji kecocokan chi-kuadrat di Excel.

Contoh: Uji kesesuaian chi-kuadrat di Excel

Seorang pemilik toko mengatakan bahwa jumlah pelanggan yang datang ke tokonya sama setiap hari dalam seminggu. Untuk menguji hipotesis ini, seorang peneliti independen mencatat jumlah pelanggan yang datang ke toko pada minggu tertentu dan menemukan hal berikut:

• Senin: 50 pelanggan
• Selasa: 60 pelanggan
• Rabu: 40 pelanggan
• Kamis: 47 pelanggan
• Jumat: 53 pelanggan

Kami akan menggunakan langkah-langkah berikut untuk melakukan uji kesesuaian chi-kuadrat untuk menentukan apakah data konsisten dengan klaim pemilik toko.

Langkah 1: Masukkan datanya.

Pertama, kita akan memasukkan nilai data untuk jumlah pelanggan yang diharapkan setiap hari di satu kolom dan jumlah pelanggan yang diamati setiap hari di kolom lain:

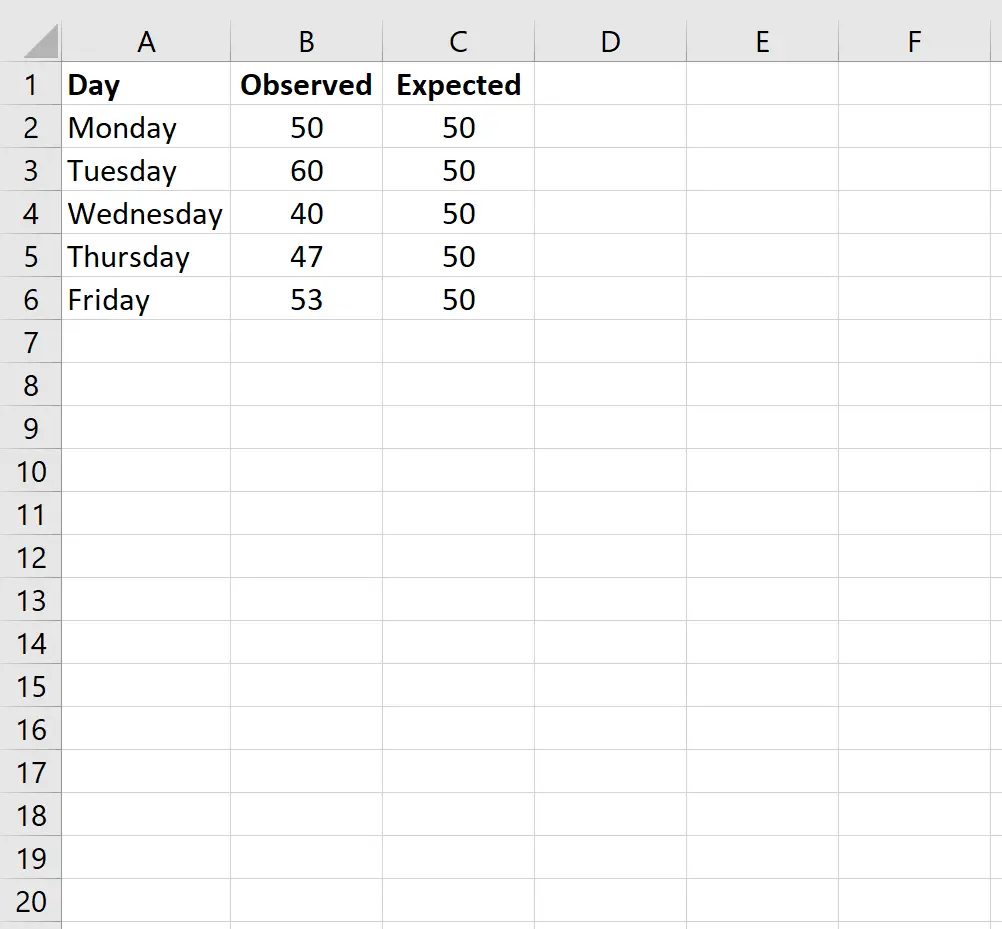
Catatan: Total ada 250 pelanggan. Jadi, jika pemilik toko mengharapkan jumlah pelanggan yang sama masuk ke tokonya setiap hari, dia memperkirakan akan mendapat 50 pelanggan per hari.

Langkah 2: Temukan perbedaan antara nilai yang diamati dan yang diharapkan.

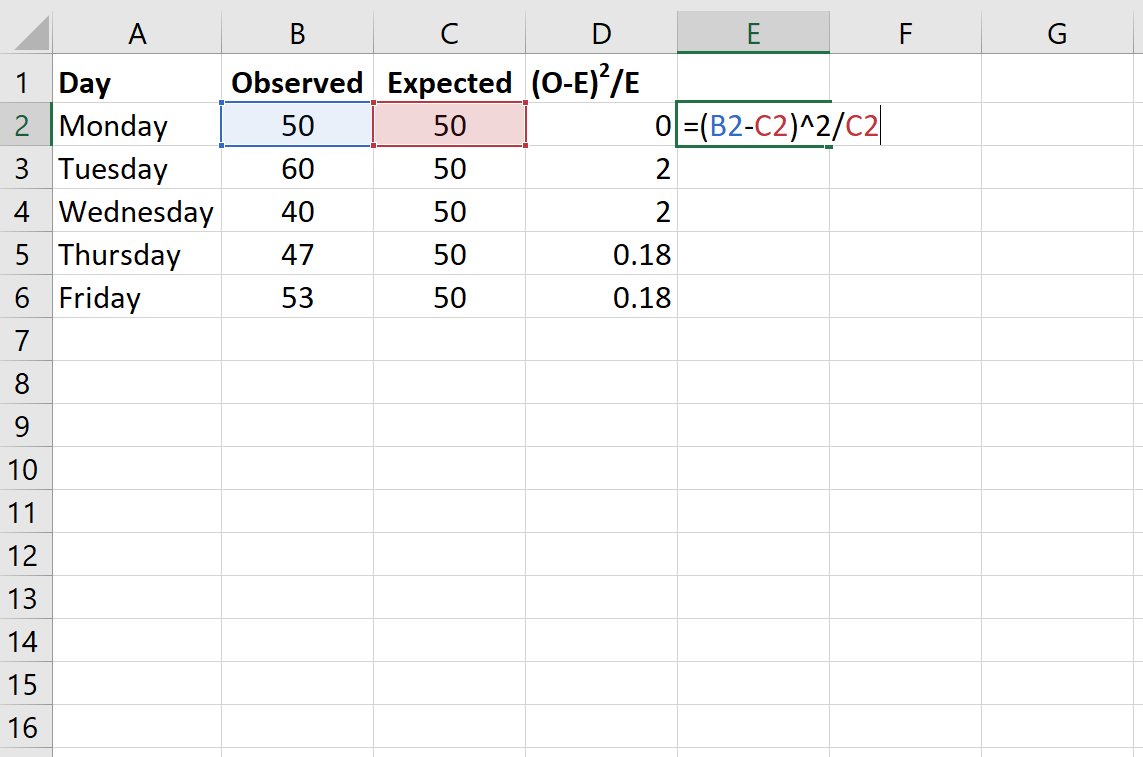
Statistik uji Chi-square untuk uji goodness-of-fit adalah X ² = Σ(OE) ² / E.

Emas:

• Σ: adalah simbol mewah yang berarti “jumlah”
• O: nilai yang diamati
• E: nilai yang diharapkan

Rumus berikut menunjukkan cara menghitung (OE) ² /E untuk setiap baris:

Langkah 3: Hitung statistik uji chi-kuadrat dan nilai p yang sesuai.

Terakhir, kami akan menghitung statistik uji Chi-kuadrat serta nilai p yang sesuai menggunakan rumus berikut:

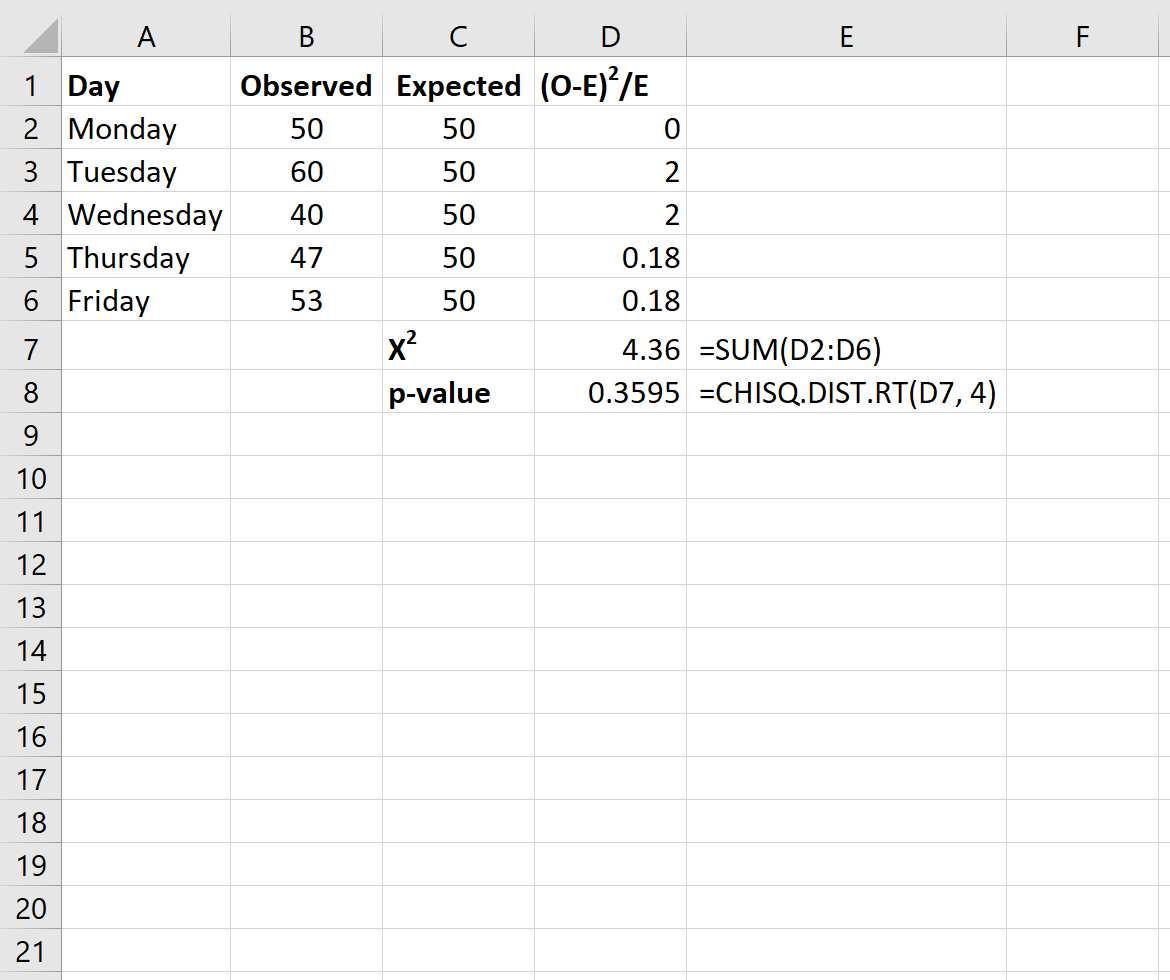
Catatan: Fungsi Excel CHISQ.DIST.RT(x, deg_freedom) mengembalikan probabilitas yang tepat dari distribusi Chi-kuadrat yang terkait dengan statistik uji x dan derajat kebebasan tertentu. Derajat kebebasan dihitung sebagai n-1. Dalam hal ini, derajat_kebebasan = 5 – 1 = 4.

Langkah 4: Interpretasikan hasilnya.

Statistik uji ^X2 untuk tes ini adalah 4,36 dan nilai p yang sesuai adalah 0,3595 . Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Artinya, kami tidak memiliki cukup bukti untuk mengatakan bahwa sebaran pelanggan sebenarnya berbeda dengan yang dilaporkan oleh pemilik toko.