Cara melakukan uji korelasi di r (dengan contoh)

Salah satu cara untuk mengukur hubungan antara dua variabel adalah dengan menggunakan koefisien korelasi Pearson , yang merupakan ukuran hubungan linier antara dua variabel .

Itu selalu mengambil nilai antara -1 dan 1 di mana:

• -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
• 0 menunjukkan tidak ada korelasi linier antara dua variabel
• Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel

Untuk menentukan apakah koefisien korelasi signifikan secara statistik, Anda dapat menghitung skor-t dan nilai-p yang sesuai.

Rumus untuk menghitung t-score suatu koefisien korelasi (r) adalah:

t = r * √ n-2 / √ 1-r ²

Nilai p dihitung sebagai nilai p dua sisi yang sesuai untuk distribusi t dengan n-2 derajat kebebasan.

Contoh: uji korelasi pada R

Untuk menentukan apakah koefisien korelasi antara dua variabel signifikan secara statistik, Anda dapat melakukan uji korelasi di R menggunakan sintaks berikut:

cor.test(x, y, metode=c(“pearson”, “kendall”, “tombak”))

Emas:

• x, y: vektor data digital.
• metode: Metode yang digunakan untuk menghitung korelasi antara dua vektor. Standarnya adalah “Pearson”.

Misalnya, kita mempunyai dua vektor berikut di R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Sebelum melakukan uji korelasi antara kedua variabel, kita dapat membuat diagram sebar cepat untuk memvisualisasikan hubungannya:

 #create scatterplot
plot(x, y, pch= 16 )

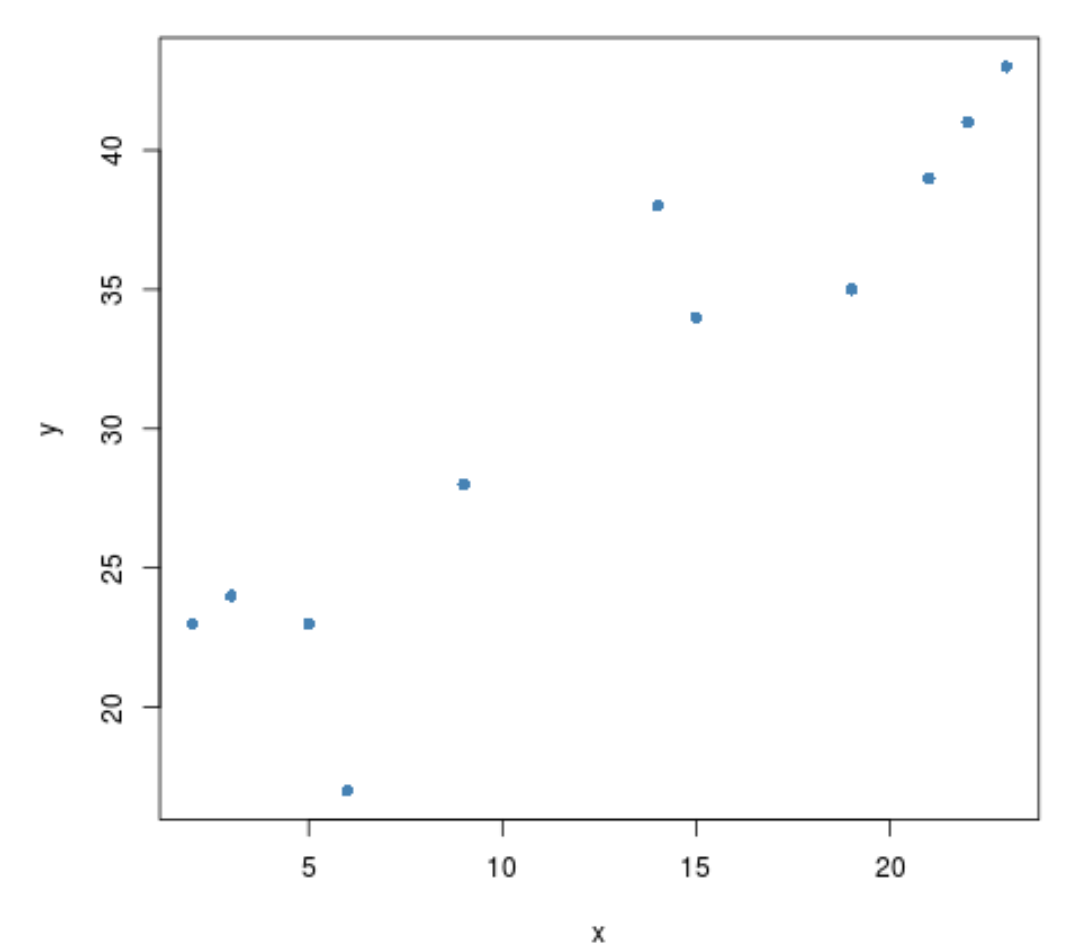
Tampaknya terdapat korelasi positif antara kedua variabel tersebut. Artinya, ketika satu meningkat, maka yang lain cenderung meningkat juga.

Untuk melihat apakah korelasi ini signifikan secara statistik, kita dapat melakukan uji korelasi:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Koefisien korelasi kedua vektor tersebut ternyata sebesar 0,9279869 .

Statistik ujinya ternyata 7,8756 dan nilai p yang sesuai adalah 1,35e-05 .

Karena nilai ini kurang dari 0,05, kami mempunyai cukup bukti untuk mengatakan bahwa korelasi antara kedua variabel signifikan secara statistik.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang koefisien korelasi:

Pengantar Koefisien Korelasi Pearson
Apa yang dianggap sebagai korelasi “kuat”?
Lima hipotesis korelasi Pearson