Cara melakukan uji normalitas di excel (langkah demi langkah)

Banyak uji statistik yang berasumsi bahwa nilai-nilai dalam suatu kumpulan data terdistribusi normal .

Salah satu cara paling sederhana untuk menguji hipotesis ini adalah dengan melakukan uji Jarque-Bera , yaitu uji goodness-of-fit yang menentukan apakah data sampel menunjukkan skewness dan kurtosis yang konsisten dengan distribusi normal.

Pengujian ini menggunakan asumsi berikut:

H ₀ : Data berdistribusi normal.

H _A : Data tidak berdistribusi normal.

Statistik uji JB didefinisikan sebagai:

JB =(n/6) * (S ² + (C ² /4))

Emas:

• n : jumlah observasi dalam sampel
• S: asimetri sampel
• C: sampel yang bagus

Berdasarkan hipotesis normalitas nol, JB ~ X ² (2).

Jika p-value yang sesuai dengan statistik uji berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa data tidak berdistribusi normal.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan pengujian Jarque-Bera untuk kumpulan data tertentu di Excel.

Langkah 1: Buat datanya

Pertama, mari buat kumpulan data palsu dengan 15 nilai:

Langkah 2: Hitung statistik pengujian

Selanjutnya menghitung statistik uji JB. Kolom E menunjukkan rumus yang digunakan:

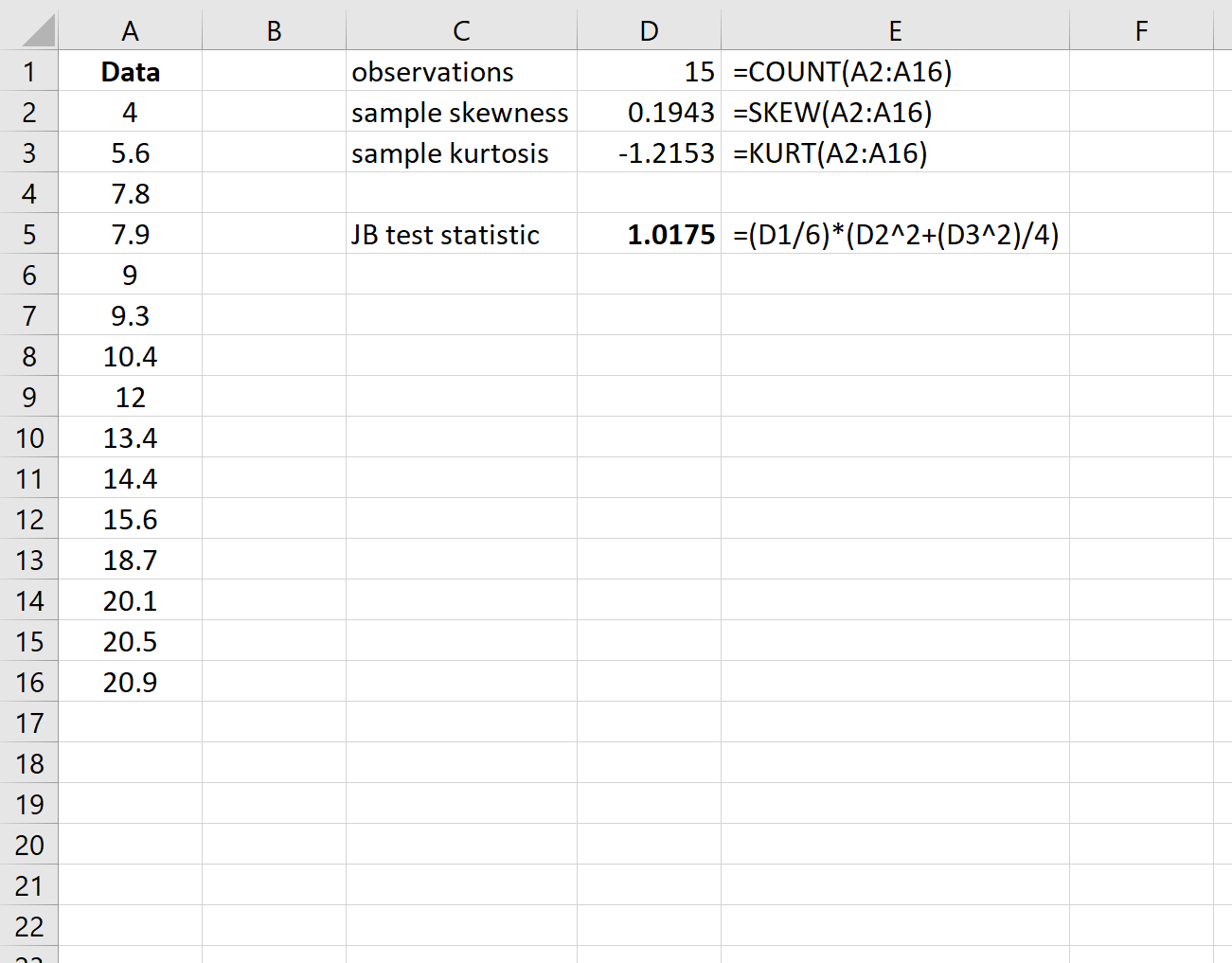
Statistik pengujiannya ternyata 1,0175 .

Langkah 3: Hitung nilai P

Berdasarkan hipotesis normalitas nol, statistik uji JB mengikuti distribusi Chi-kuadrat dengan 2 derajat kebebasan.

Jadi, untuk mencari nilai p untuk pengujian tersebut, kita akan menggunakan fungsi berikut di Excel: =CHISQ.DIST.RT(Statistik pengujian JB, 2)

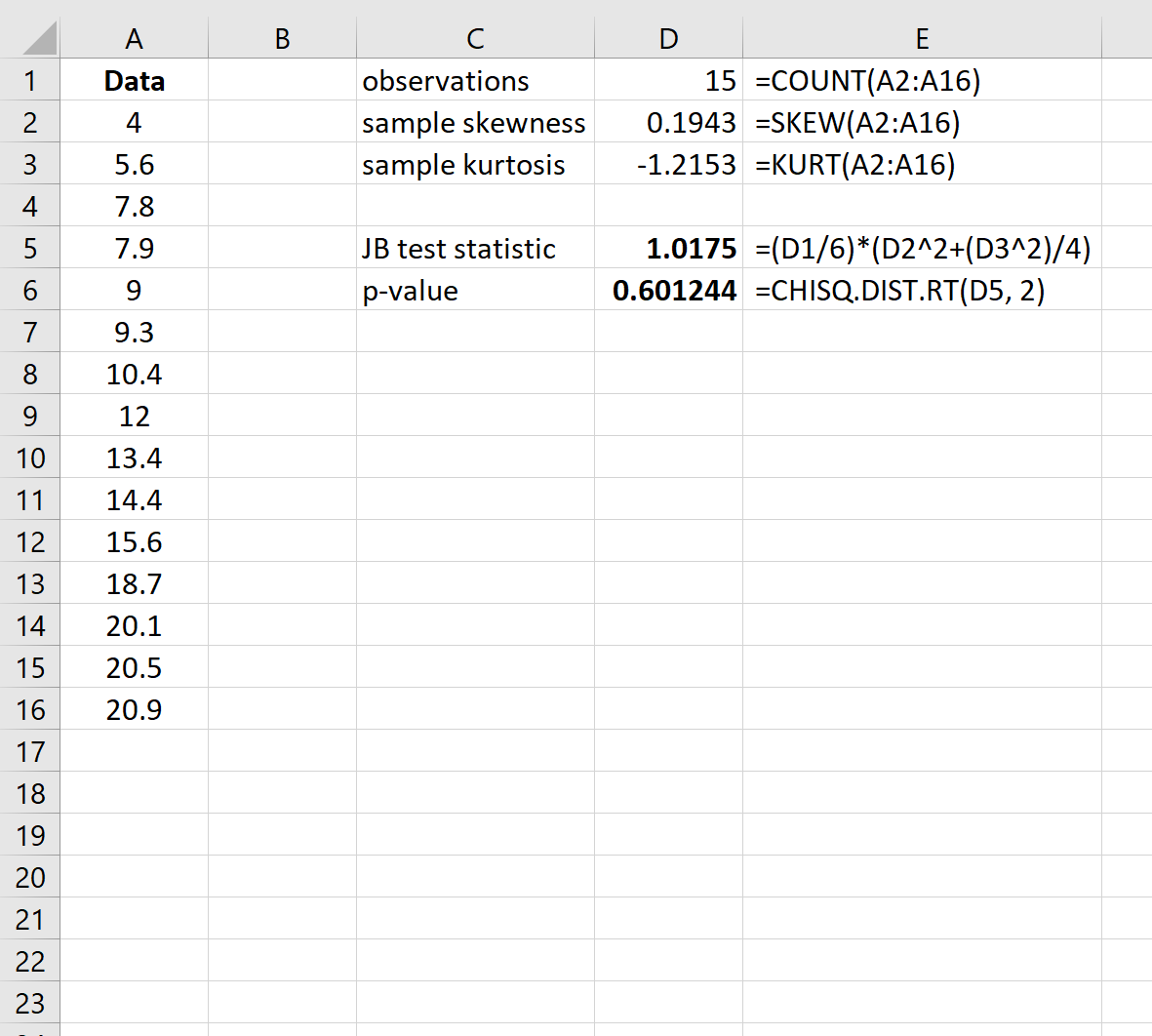
Nilai p dari tes ini adalah 0,601244 . Karena nilai p ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa kumpulan data tidak terdistribusi secara normal.

Dengan kata lain, data dapat diasumsikan berdistribusi normal.

Sumber daya tambahan

Cara Membuat Plot QQ di Excel
Cara Melakukan Uji Kesesuaian Chi Kuadrat di Excel