Cara menguji normalitas dengan python (4 metode)

Banyak uji statistik mengasumsikan bahwa kumpulan data terdistribusi normal.

Ada empat cara umum untuk memeriksa hipotesis ini dengan Python:

1. (Metode visual) Membuat histogram.

• Jika histogram kira-kira berbentuk “lonceng”, maka data diasumsikan terdistribusi normal.

2. (Metode visual) Buat plot QQ.

• Jika titik-titik pada plot terletak kira-kira sepanjang garis lurus diagonal, maka data diasumsikan berdistribusi normal.

3. (Uji statistik formal) Lakukan uji Shapiro-Wilk.

• Jika p-value uji lebih besar dari α = 0,05 maka data diasumsikan berdistribusi normal.

4. (Uji statistik formal) Lakukan uji Kolmogorov-Smirnov.

• Jika p-value uji lebih besar dari α = 0,05 maka data diasumsikan berdistribusi normal.

Contoh berikut menunjukkan cara menggunakan masing-masing metode ini dalam praktik.

Metode 1: Buat Histogram

Kode berikut menunjukkan cara membuat histogram untuk kumpulan data yang mengikuti distribusi log-normal :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

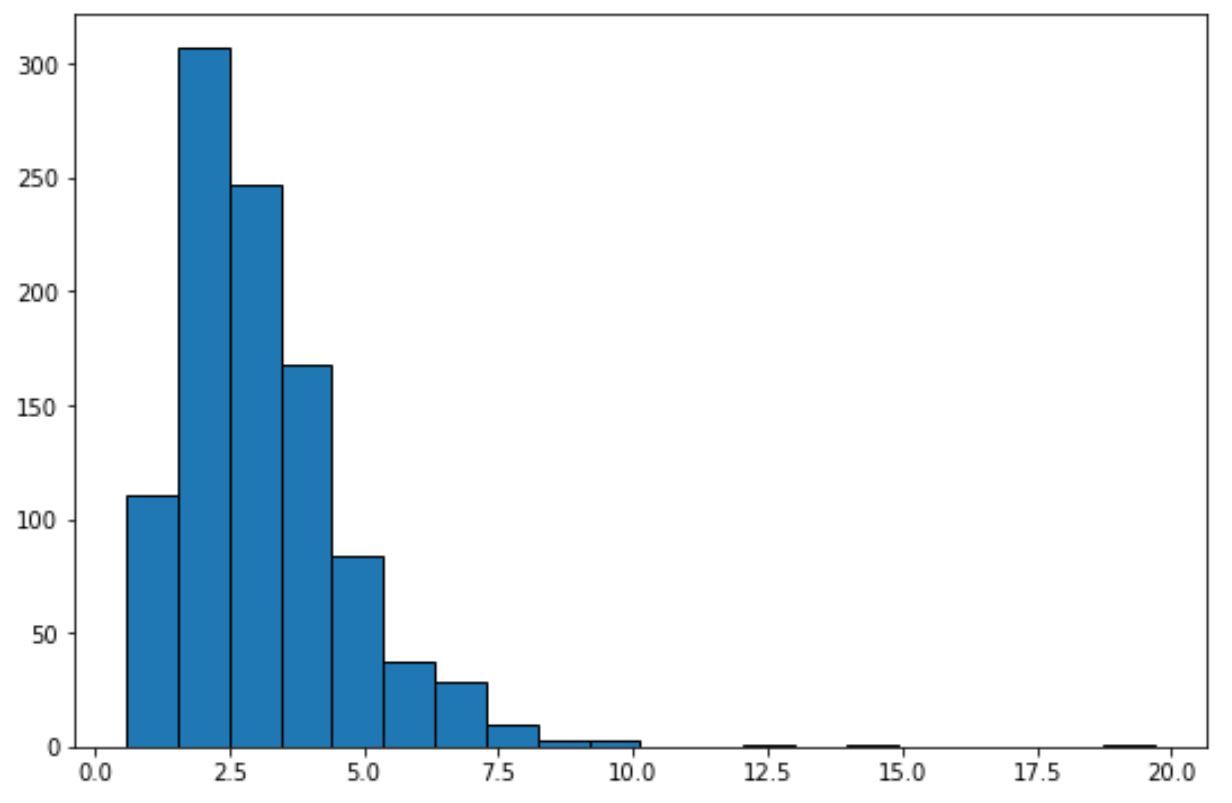
Hanya dengan melihat histogram ini, kita dapat mengetahui bahwa kumpulan data tidak menunjukkan “bentuk lonceng” dan tidak terdistribusi secara normal.

Metode 2: Buat Plot QQ

Kode berikut menunjukkan cara membuat plot QQ untuk kumpulan data yang mengikuti distribusi log-normal:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

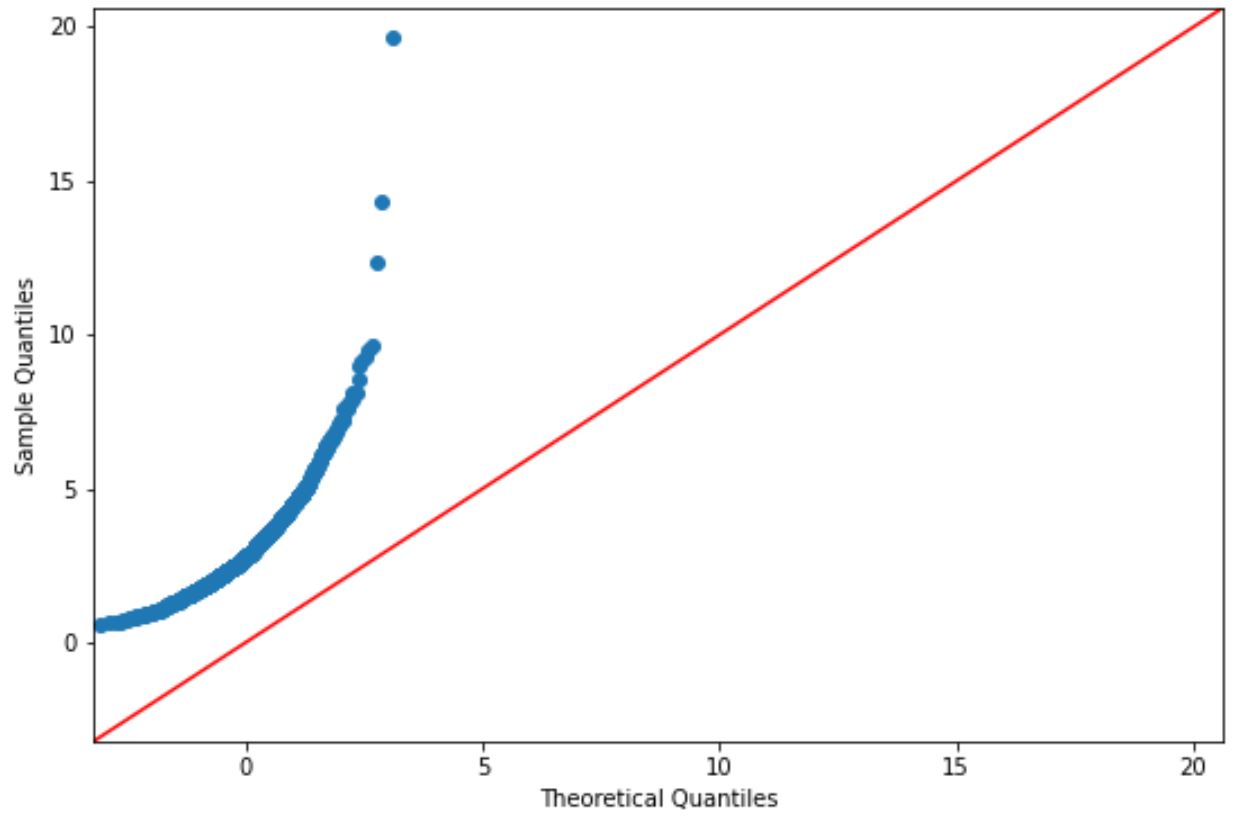
Jika titik plot terletak kira-kira di sepanjang garis lurus diagonal, secara umum kita berasumsi bahwa kumpulan data terdistribusi normal.

Namun titik-titik pada grafik ini jelas tidak sesuai dengan garis merah, sehingga kita tidak dapat berasumsi bahwa kumpulan data ini berdistribusi normal.

Ini seharusnya masuk akal mengingat kami menghasilkan data menggunakan fungsi distribusi log-normal.

Metode 3: Lakukan tes Shapiro-Wilk

Kode berikut menunjukkan cara melakukan Shapiro-Wilk untuk kumpulan data yang mengikuti distribusi log-normal:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Dari hasilnya, kita dapat melihat bahwa statistik pengujian adalah 0,857 dan nilai p yang sesuai adalah 3,88e-29 (sangat mendekati nol).

Karena nilai p kurang dari 0,05, kami menolak hipotesis nol uji Shapiro-Wilk.

Artinya kita mempunyai cukup bukti untuk mengatakan bahwa data sampel tidak berasal dari distribusi normal.

Metode 4: Lakukan tes Kolmogorov-Smirnov

Kode berikut menunjukkan cara melakukan pengujian Kolmogorov-Smirnov untuk kumpulan data yang mengikuti distribusi log-normal:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Dari hasilnya, kita dapat melihat bahwa statistik uji adalah 0,841 dan nilai p yang sesuai adalah 0,0 .

Karena nilai p kurang dari 0,05, kami menolak hipotesis nol uji Kolmogorov-Smirnov.

Artinya kita mempunyai cukup bukti untuk mengatakan bahwa data sampel tidak berasal dari distribusi normal.

Cara menangani data yang tidak normal

Jika kumpulan data tertentu tidak terdistribusi normal, kita sering kali dapat melakukan salah satu transformasi berikut untuk membuatnya lebih terdistribusi normal:

1. Transformasi log: ubah nilai x menjadi log(x) .

2. Transformasi akar kuadrat: Ubah nilai x menjadi √x .

3. Transformasi akar pangkat tiga: ubah nilai x menjadi x ^1/3 .

Dengan melakukan transformasi ini, kumpulan data secara umum menjadi lebih terdistribusi secara normal.

Baca tutorial ini untuk melihat cara melakukan transformasi ini dengan Python.