Uji-t sampel berpasangan: definisi, rumus dan contoh
Uji-t sampel berpasangan digunakan untuk membandingkan rata-rata dua sampel ketika setiap observasi pada satu sampel dapat dikaitkan dengan observasi pada sampel lainnya.
Tutorial ini menjelaskan hal berikut:
- Motivasi untuk melakukan uji-t sampel berpasangan.
- Rumus untuk melakukan uji-t sampel berpasangan.
- Asumsi yang harus dipenuhi untuk melakukan uji t sampel berpasangan.
- Contoh cara melakukan uji-t sampel berpasangan.
Uji-t sampel berpasangan: Motivasi
Uji-t sampel berpasangan biasanya digunakan dalam dua skenario:
1. Pengukuran dilakukan pada subjek sebelum dan sesudah perlakuan – misalnya, lompatan vertikal maksimum pemain bola basket perguruan tinggi diukur sebelum dan sesudah partisipasi mereka dalam program pelatihan.
2. Pengukuran dilakukan dalam dua kondisi berbeda – misalnya, waktu respons pasien diukur dengan dua obat berbeda.
Dalam kedua kasus tersebut, kami ingin membandingkan pengukuran rata-rata antara dua kelompok di mana setiap observasi dari satu sampel dapat dikaitkan dengan observasi dari sampel lainnya.
Uji-t sampel berpasangan: rumus
Uji-t sampel berpasangan selalu menggunakan hipotesis nol berikut:
- H 0 : μ 1 = μ 2 (rata-rata kedua populasi adalah sama)
Hipotesis alternatif dapat bersifat bilateral, kiri atau kanan:
- H 1 (dua sisi): μ 1 ≠ μ 2 (rata-rata kedua populasi tidak sama)
- H 1 (kiri): μ 1 < μ 2 (rata-rata populasi 1 lebih rendah dibandingkan rata-rata populasi 2)
- H 1 (kanan): μ 1 > μ 2 (rata-rata populasi 1 lebih besar dari rata-rata populasi 2)
Kami menggunakan rumus berikut untuk menghitung statistik uji-t:
t = x beda / (s beda /√n)
Emas:
- x diff : contoh selisih rata-rata
- s : contoh simpangan baku selisih
- n: ukuran sampel (yaitu jumlah pasangan)
Jika nilai p yang sesuai dengan statistik uji-t dengan derajat kebebasan (n-1) lebih kecil dari tingkat signifikansi yang dipilih (pilihan umum adalah 0,10, 0,05, dan 0,01), maka Anda dapat menolak hipotesis nol.
Uji-t sampel berpasangan: asumsi
Agar hasil uji-t sampel berpasangan valid, asumsi-asumsi berikut harus dipenuhi:
- Peserta harus dipilih secara acak dari populasi.
- Perbedaan antar pasangan harus terdistribusi secara normal.
- Seharusnya tidak ada perbedaan yang ekstrim.
Uji -t sampel berpasangan : contoh
Misalkan kita ingin mengetahui apakah suatu program latihan tertentu mampu meningkatkan lompatan vertikal maksimum (dalam inci) pemain bola basket perguruan tinggi atau tidak.
Untuk mengujinya, kita dapat merekrut sampel acak sederhana yang terdiri dari 20 pemain bola basket perguruan tinggi dan mengukur setiap lompatan vertikal maksimum mereka. Kemudian kita dapat meminta setiap pemain menggunakan program pelatihan selama sebulan dan kemudian mengukur lompatan vertikal maksimum mereka lagi pada akhir bulan tersebut.

Untuk menentukan apakah program latihan benar-benar berpengaruh terhadap lompatan vertikal maksimum, kami akan melakukan uji-t sampel berpasangan pada tingkat signifikansi α = 0,05 dengan menggunakan langkah-langkah berikut:
Langkah 1: Hitung data ringkasan untuk perbedaannya.
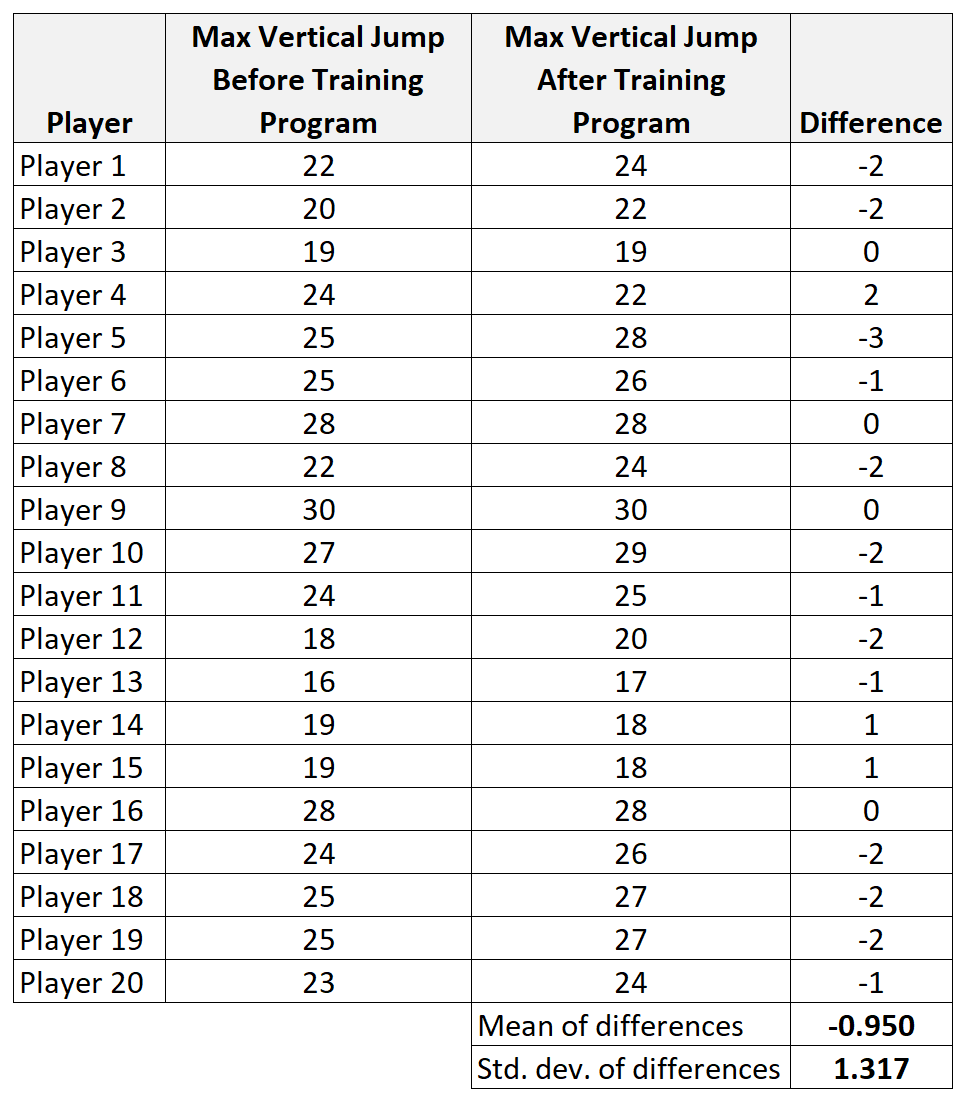
- x diff : rata-rata sampel selisih = -0,95
- s: standar deviasi sampel selisih = 1,317
- n: ukuran sampel (yaitu jumlah pasangan) = 20
Langkah 2: Tentukan asumsi.
Kami akan melakukan uji-t untuk sampel berpasangan dengan hipotesis berikut:
- H 0 : μ 1 = μ 2 (rata-rata kedua populasi adalah sama)
- H 1 : μ 1 ≠ μ 2 (rata-rata dua populasi tidak sama)
Langkah 3: Hitung statistik uji- t .
t = x perbedaan / (s perbedaan /√n) = -0,95 / (1,317/ √ 20) = -3,226
Langkah 4: Hitung nilai p dari statistik uji -t .
Menurut kalkulator skor T ke Nilai P , nilai p yang terkait dengan t = -3,226 dan derajat kebebasan = n-1 = 20-1 = 19 adalah 0,00445 .
Langkah 5: Buatlah kesimpulan.
Karena nilai p ini berada di bawah tingkat signifikansi α = 0,05, kami menolak hipotesis nol. Kami memiliki cukup bukti yang mengatakan bahwa rata-rata lompatan vertikal maksimum pemain sebelum dan sesudah mengikuti program latihan berbeda.
Catatan: Anda juga dapat melakukan uji-t sampel berpasangan secara keseluruhan hanya dengan menggunakan kalkulator uji-t sampel berpasangan .
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan uji-t sampel berpasangan menggunakan program statistik yang berbeda:
Cara melakukan uji-t sampel berpasangan di Excel
Cara melakukan uji-t sampel berpasangan di SPSS
Cara melakukan uji-t sampel berpasangan di Stata
Cara Melakukan Uji-t Sampel Berpasangan pada Kalkulator TI-84
Cara melakukan uji-t sampel berpasangan di R
Cara melakukan uji-t sampel berpasangan dengan Python
Cara Melakukan Uji-T Sampel Berpasangan dengan Tangan