Cara menguji signifikansi kemiringan regresi

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan luas persegi dan harga 12 rumah berbeda:

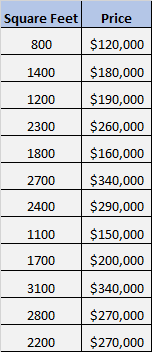
Kami ingin tahu apakah ada hubungan yang signifikan antara luas persegi dan harga.

Untuk mendapatkan gambaran seperti apa datanya, pertama-tama kita membuat plot sebar dengan kaki persegi pada sumbu x dan harga pada sumbu y:

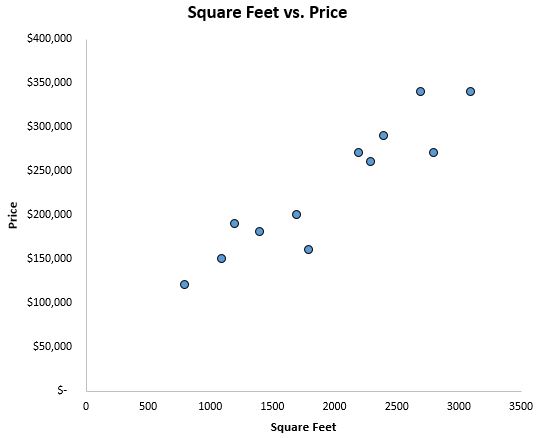
Kita dapat dengan jelas melihat bahwa ada korelasi positif antara luas persegi dan harga. Seiring bertambahnya luas persegi, harga rumah juga cenderung meningkat.

Namun, untuk mengetahui apakah terdapat hubungan yang signifikan secara statistik antara luas persegi dan harga, kita perlu menjalankan regresi linier sederhana.

Jadi kita menjalankan regresi linier sederhana menggunakan kaki persegi sebagai prediktor dan harga sebagai respon dan mendapatkan hasil sebagai berikut:

Baik Anda menjalankan regresi linier sederhana di Excel, SPSS, R, atau perangkat lunak lainnya, Anda akan mendapatkan hasil yang mirip dengan yang ditunjukkan di atas.

Ingatlah bahwa regresi linier sederhana akan menghasilkan garis yang paling sesuai, yaitu persamaan garis yang paling “sesuai” dengan data di diagram sebar kita. Garis yang paling sesuai ini didefinisikan sebagai:

ŷ = b ₀ + b ₁ x

dimana ŷ adalah nilai prediksi variabel respon, b ₀ adalah intersep, b ₁ adalah koefisien regresi, dan x adalah nilai variabel prediktor.

Nilai b ₀ diberikan oleh koefisien asal yaitu 47588,70.

Nilai b ₁ diberikan oleh koefisien variabel prediktor Square Feet yaitu sebesar 93,57.

Jadi garis yang paling cocok dalam contoh ini adalah ŷ = 47588.70+ 93.57x

Berikut cara menafsirkan baris yang paling sesuai ini:

• b ₀ : Ketika nilai kaki persegi adalah nol, nilai harga rata-rata yang diharapkan adalah $47,588.70. (Dalam hal ini tidak masuk akal untuk menafsirkan intersep tersebut, karena sebuah rumah tidak akan pernah memiliki luas nol kaki persegi)
• b ₁ : Untuk setiap tambahan kaki persegi, rata-rata perkiraan kenaikan harga adalah $93,57.

Jadi, sekarang kita tahu bahwa untuk setiap tambahan kaki persegi, rata-rata perkiraan kenaikan harga adalah $93,57.

Untuk mengetahui apakah peningkatan ini signifikan secara statistik, kita perlu melakukan uji hipotesis untuk _B1 atau membuat interval kepercayaan untuk _B1 .

Catatan : Uji hipotesis dan selang kepercayaan akan selalu memberikan hasil yang sama.

Konstruksi interval kepercayaan untuk kemiringan regresi

Untuk membuat interval kepercayaan kemiringan regresi, kami menggunakan rumus berikut:

Interval kepercayaan = b ₁ +/- (t _{1-∝/2, n-2} ) * (kesalahan standar b ₁ )

Emas:

• b ₁ adalah koefisien kemiringan yang diberikan dalam hasil regresi
• (t _{1-∝/2, n-2} ) adalah nilai t kritis untuk tingkat kepercayaan 1-∝ dengan n-2 derajat kebebasan di mana n adalah jumlah total observasi dalam kumpulan data kami
• (kesalahan standar b ₁ ) adalah kesalahan standar b ₁ yang diberikan dalam hasil regresi

Sebagai contoh, berikut adalah cara membuat interval kepercayaan 95% untuk B ₁ :

• b ₁ adalah 93,57 dari keluaran regresi.
• Karena kita menggunakan selang kepercayaan 95%, ∝ = 0,05 dan n-2 = 12-2 = 10, maka t _{0,975, 10} adalah 2,228 berdasarkan tabel distribusi t
• (standar error _b1 ) adalah 11,45 dari keluaran regresi

Jadi, selang kepercayaan 95% kita untuk _B1 adalah:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Ini berarti kami 95% yakin bahwa kenaikan harga rata-rata sebenarnya untuk setiap tambahan kaki persegi adalah antara $68,06 dan $119,08.

Perhatikan bahwa $0 tidak berada dalam interval ini, sehingga hubungan antara luas persegi dan harga signifikan secara statistik pada tingkat kepercayaan 95%.

Melakukan uji hipotesis untuk kemiringan regresi

Untuk melakukan uji hipotesis kemiringan regresi, kami mengikuti lima langkah standar untuk setiap uji hipotesis :

Langkah 1. Nyatakan hipotesisnya.

Hipotesis nol (H0): B ₁ = 0

Hipotesis alternatif: (Ha): B ₁ ≠ 0

Langkah 2. Tentukan tingkat signifikansi yang akan digunakan.

Karena kita membangun interval kepercayaan 95% pada contoh sebelumnya, kita akan menggunakan pendekatan yang setara di sini dan memilih untuk menggunakan tingkat signifikansi 0,05.

Langkah 3. Temukan statistik uji dan nilai p yang sesuai.

Dalam hal ini statistik ujinya adalah t = koefisien b ₁ / kesalahan standar b ₁ dengan n-2 derajat kebebasan. Nilai-nilai ini dapat kita temukan dari hasil regresi:

Jadi, statistik uji t = 92,89 / 13,88 = 6,69.

Menggunakan kalkulator T score to P value dengan skor 6,69 dengan 10 derajat kebebasan dan uji dua sisi diperoleh nilai p = 0,000 .

Langkah 4. Tolak atau jangan tolak hipotesis nol.

Karena nilai p berada di bawah tingkat signifikansi 0,05, kami menolak hipotesis nol.

Langkah 5. Interpretasikan hasilnya.

Karena kami menolak hipotesis nol, kami mempunyai cukup bukti untuk mengatakan bahwa rata-rata kenaikan harga sebenarnya untuk setiap tambahan kaki persegi tidaklah nol.