Uji t berpasangan atau tidak berpasangan: apa bedanya?
Dalam statistik, ada dua jenis uji-t dua sampel :
Uji-t berpasangan: Digunakan untuk membandingkan rata-rata dua sampel ketika masing-masing individu dalam satu sampel juga muncul di sampel lainnya.
Uji-t tidak berpasangan: digunakan untuk membandingkan rata-rata dua sampel ketika setiap individu dalam satu sampel tidak bergantung pada setiap individu dalam sampel lainnya.
Catatan: Uji-t tidak berpasangan lebih sering disebut uji-t sampel independen.
Misalnya, seorang profesor ingin menentukan apakah dua teknik belajar yang berbeda menghasilkan nilai rata-rata ujian yang berbeda atau tidak.
Untuk melakukan uji-t berpasangan , ia dapat merekrut 10 siswa dan meminta mereka menggunakan satu teknik belajar selama satu bulan dan mengikuti ujian, kemudian meminta mereka menggunakan teknik belajar kedua selama satu bulan dan mengikuti ujian lain dengan tingkat kesulitan yang sama.
Seperti inilah tampilan datanya:
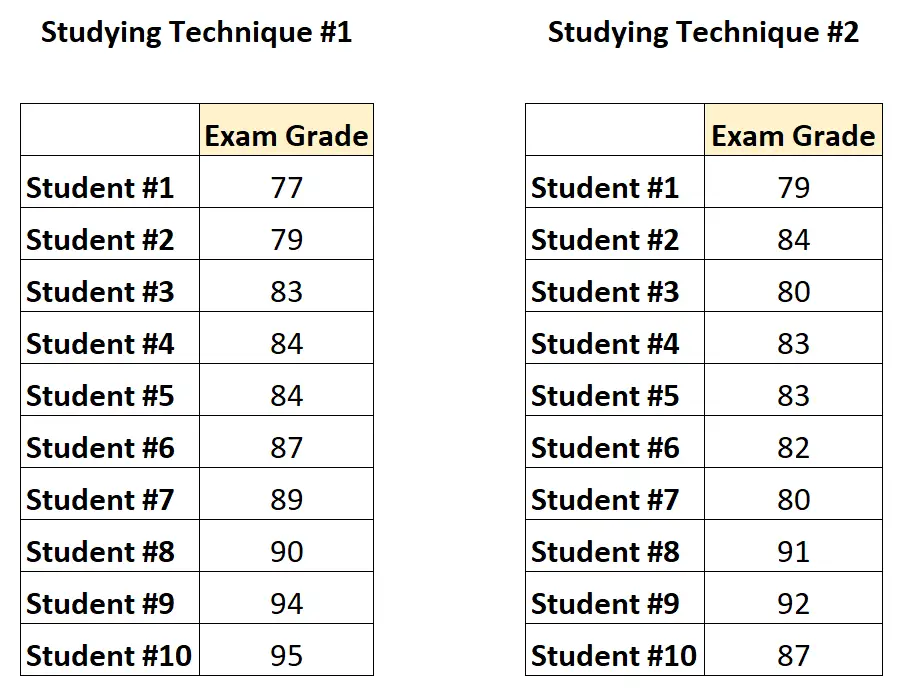
Karena setiap siswa muncul di setiap kelompok, profesor akan melakukan uji-t berpasangan untuk menentukan apakah nilai rata-rata antara kedua kelompok berbeda.
Untuk melakukan uji-t tidak berpasangan , ia dapat merekrut total 20 siswa dan secara acak membagi mereka menjadi dua kelompok yang terdiri dari 10 orang. Ia dapat meminta satu kelompok untuk menggunakan teknik belajar selama satu bulan dan kelompok lainnya untuk ‘menggunakan teknik belajar kedua selama satu bulan. sebulan. bulan dan minta semua siswa mengikuti ujian yang sama.
Seperti inilah tampilan datanya:
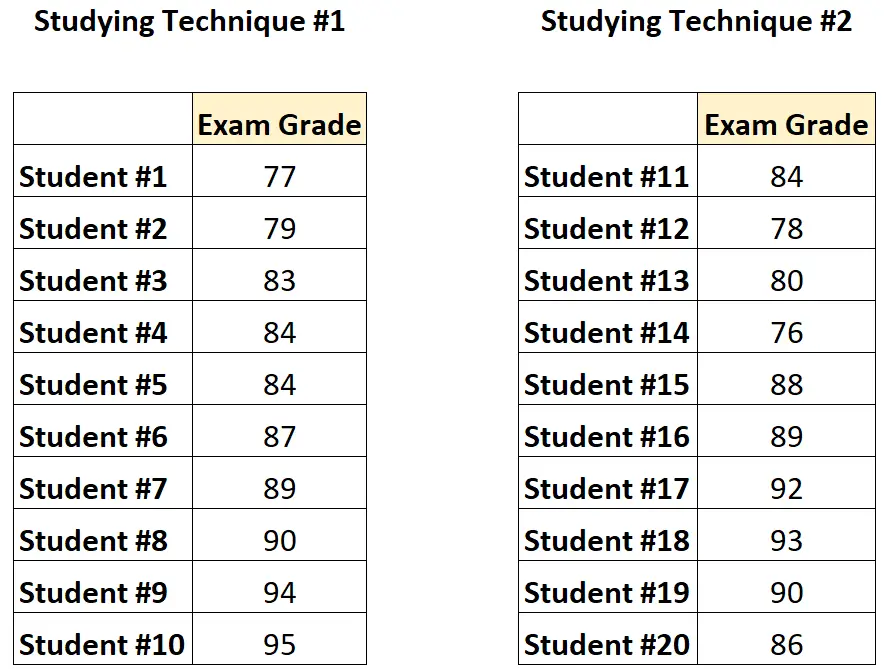
Karena siswa dalam satu kelompok benar-benar independen terhadap siswa di kelompok lain, profesor akan melakukan uji-t tidak berpasangan untuk menentukan apakah nilai rata-rata antara kedua kelompok berbeda.
Hipotesis
Uji-t berpasangan dan tidak berpasangan membuat asumsi berikut:
- Data dari kedua sampel diperoleh dengan menggunakan metode random sampling .
- Data dari kedua sampel harus terdistribusi normal.
- Seharusnya tidak ada outlier yang ekstrim pada kedua sampel.
Asumsi ini harus diverifikasi sebelum melakukan uji-t untuk memastikan keandalan hasil pengujian.
Keuntungan dan kerugian
Uji t berpasangan menawarkan keuntungan sebagai berikut:
- Diperlukan sampel yang lebih kecil. Perhatikan bahwa uji-t berpasangan pada contoh sebelumnya hanya memerlukan total 10 siswa, sedangkan uji-t tidak berpasangan memerlukan total 20 siswa.
- Setiap sampel berisi individu-individu dengan karakteristik yang sama. Kedua kelompok dijamin memiliki individu dengan kemampuan, kecerdasan, dll. sama karena individu yang sama muncul di setiap kelompok.
Namun, uji-t berpasangan mempunyai potensi kelemahan sebagai berikut:
- Potensi pengurangan ukuran sampel. Jika seorang individu keluar dari penelitian, ukuran sampel setiap kelompok dikurangi satu sejak individu tersebut muncul di setiap kelompok.
- Potensi efek pesanan. Efek urutan mengacu pada perbedaan hasil antara kedua kelompok karena urutan perlakuan yang diberikan kepada individu. Misalnya, seseorang mungkin berprestasi lebih baik pada ujian kedua hanya karena mereka meningkatkan keterampilan mengerjakan ujian, bukan karena teknik belajarnya.
Ingatlah pro dan kontra ini ketika memutuskan apakah akan menggunakan uji t berpasangan atau tidak berpasangan.
Sumber daya tambahan
Simak tutorial berikut untuk lebih memahami uji-t berpasangan:
Dan gunakan tutorial berikut untuk lebih memahami uji-t tidak berpasangan (alias uji-t sampel independen):
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya