Ukuran sampel
Artikel ini menjelaskan apa itu ukuran sampel dan mengapa itu penting dalam statistik. Selain itu, Anda akan menemukan cara menghitung ukuran sampel yang sesuai dan latihan yang diselesaikan sehingga Anda dapat melihat cara melakukannya.
Berapa ukuran sampelnya?
Ukuran sampel (atau ukuran sampel ) adalah jumlah individu yang menjadi sampel penelitian. Dalam statistik, ukuran sampel penting agar sampel dapat mewakili keseluruhan populasi.
Oleh karena itu, ukuran sampel suatu penelitian statistik harus cukup besar untuk mewakili karakteristik seluruh populasi. Di sisi lain, ukuran sampel tidak boleh terlalu besar, karena penelitian menjadi lebih mahal. Kesimpulannya, ukuran sampel harus memadai, tidak terlalu besar dan tidak terlalu kecil.
Misalnya kita ingin melakukan analisis ketinggian suatu negara, kita tidak bisa menanyakan tinggi badan seluruh penduduk negara tersebut, karena surveinya akan memakan waktu lama dan biaya yang terlalu mahal. Oleh karena itu perlu dilakukan pengambilan sampel secara acak dan mewawancarai sampel yang mewakili populasi saja.
Dan bagaimana kita bisa mengetahui ukuran sampel yang tepat? Pada bagian selanjutnya, kita akan melihat bagaimana menentukan ukuran sampel yang sesuai berdasarkan kebutuhan penelitian.
Cara menghitung ukuran sampel
Untuk memperkirakan mean, ukuran sampel yang diperlukan sama dengan kuadrat Z α/2 dikalikan dengan deviasi standar (σ) dibagi dengan margin kesalahan yang diinginkan (e). Oleh karena itu , rumus untuk menghitung ukuran sampel adalah:
![]()
Emas:
-

adalah ukuran sampel.
-
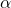
adalah tingkat signifikansi yang diinginkan. Mempertimbangkan hal ini
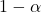
adalah tingkat kepercayaan yang diinginkan.
-

adalah kuantil dari distribusi normal standar yang sesuai dengan probabilitas α/2. Untuk ukuran sampel besar dan tingkat kepercayaan 95% biasanya mendekati 1,96 dan untuk tingkat kepercayaan 99% biasanya mendekati 2,576.
-

adalah simpangan baku.
Perlu diingat bahwa dalam rumus ini diasumsikan jumlah populasi tidak terhingga, yaitu jumlah populasi sangat besar atau tidak diketahui.
Catatan: Rumus di atas diturunkan dari interval rumus kepercayaan mean .
Contoh perhitungan ukuran sampel
Di bagian ini, kami akan menghitung ukuran sampel yang sesuai untuk survei statistik sebagai contoh.
- Kita tahu bahwa standar deviasi suatu populasi adalah sekitar 15, tapi kita tidak tahu meannya, jadi kita ingin melakukan penelitian untuk memperkirakan meannya. Berapa ukuran sampel yang kita perlukan jika kita menginginkan margin of error ±2 dengan tingkat kepercayaan 95%?
Seperti yang kita lihat di atas, rumus menghitung ukuran sampel adalah:
![]()
Dalam hal ini, tingkat kepercayaan yang diinginkan adalah 95%, sehingga nilai Z α/2 yang sesuai adalah 1,96.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
Terakhir, setelah kita mengetahui nilai semua parameter, kita substitusikan nilainya ke dalam rumus dan hitung ukuran sampel:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
Singkatnya, untuk memperkirakan mean populasi dengan persyaratan yang diinginkan, kita memerlukan setidaknya sampel sebanyak 217 individu.
Ukuran sampel, tingkat kepercayaan, dan margin kesalahan
Tergantung pada tingkat kepercayaan dan margin kesalahan yang diperlukan, ukuran sampel yang diperlukan akan bervariasi. Dengan demikian, ukuran sampel, tingkat kepercayaan, dan margin kesalahan berhubungan sebagai berikut:
- Besar sampel dan tingkat kepercayaan berbanding lurus. Artinya, jika tingkat kepercayaan meningkat maka jumlah sampel juga akan meningkat.
- Ukuran sampel dan margin kesalahan berbanding terbalik. Jadi, jika margin of error bertambah maka jumlah sampel akan berkurang.
- Oleh karena itu, peningkatan ukuran sampel dapat meningkatkan tingkat kepercayaan atau mengurangi margin kesalahan.
Rumus ukuran sampel lainnya
Bergantung pada parameter yang akan diestimasi, rumus untuk ukuran sampel yang diperlukan sedikit berbeda. Oleh karena itu, pada bagian ini kita akan melihat rumus lain yang berguna untuk menghitung ukuran sampel dalam beberapa kasus khusus.
ukuran sampel suatu proporsi
Rumus untuk menghitung besar sampel yang diperlukan untuk memperkirakan suatu proporsi (p) adalah:
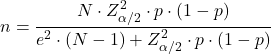
Ukuran sampel suatu probabilitas
Saat Anda ingin memperkirakan suatu probabilitas, disarankan untuk menggunakan rumus berikut untuk menentukan ukuran sampel yang diperlukan:
![]()
Ukuran sampel untuk membandingkan dua mean independen
Rumus untuk menghitung ukuran sampel ketika membandingkan dua mean independen dengan risiko α dan risiko β tertentu adalah sebagai berikut:
![]()
Emas
![]()
adalah perbedaan antara dua cara hipotesis alternatif.
Ukuran sampel untuk membandingkan dua mean berpasangan
Jika Anda ingin membandingkan dua mean berpasangan dengan error α dan error β yang tetap, rumus yang digunakan untuk mencari jumlah observasi dalam sampel adalah:
![]()
Emas
![]()
adalah perbedaan antara dua mean berpasangan dari hipotesis alternatif dan
![]()
Ini adalah varians perbedaan antara dua pengukuran pada individu yang sama.