Berapa selisih sisa? (definisi & #038; contoh)

Varians sisa (terkadang disebut “varians yang tidak dapat dijelaskan”) mengacu pada varians dalam model yang tidak dapat dijelaskan oleh variabel model.

Semakin tinggi varians residual suatu model, maka model tersebut semakin tidak mampu menjelaskan variasi data.

Varians sisa muncul pada hasil dua model statistik yang berbeda:

1. ANOVA: digunakan untuk membandingkan rata-rata tiga atau lebih kelompok independen.

2. Regresi: digunakan untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respon .

Contoh berikut menunjukkan bagaimana menafsirkan varians sisa dalam masing-masing metode.

Varians sisa dalam model ANOVA

Setiap kali kita menyesuaikan model ANOVA (“analisis varians”), kita akan mendapatkan tabel ANOVA yang terlihat seperti berikut:

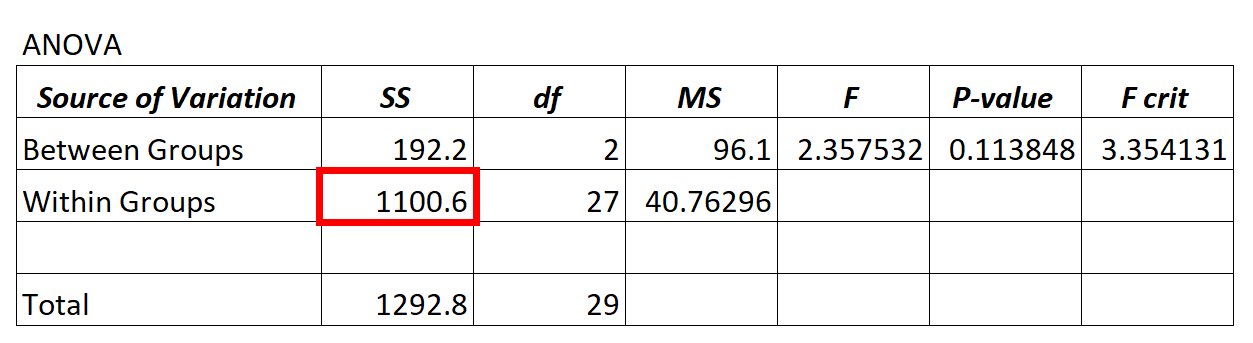
Nilai varians sisa dari model ANOVA terdapat pada kolom SS (“jumlah kuadrat”) untuk variasi dalam kelompok .

Nilai ini juga disebut “jumlah kesalahan kuadrat” dan dihitung menggunakan rumus berikut:

Σ(X _ij – Xj ₎ ²

Emas:

• Σ : simbol Yunani yang berarti “jumlah”
• X _ij : observasi ^ke-i kelompok j
• X _j : rata-rata kelompok j

Pada model ANOVA di atas terlihat variance residualnya adalah 1100,6.

Untuk menentukan apakah varians sisa ini “tinggi”, kita dapat menghitung jumlah rata-rata kuadrat dalam kelompok dan jumlah rata-rata kuadrat antar kelompok dan mencari rasio antara keduanya, yang menghasilkan nilai F keseluruhan dalam tabel ANOVA.

• F = MS _masuk / MS _masuk
• F = 96,1 / 40,76296
• F = 2,357

Nilai F pada tabel ANOVA di atas adalah 2,357 dan nilai p yang sesuai adalah 0,113848. Karena nilai p ini tidak kurang dari α = 0,05, kita tidak mempunyai cukup bukti untuk menolak hipotesis nol.

Artinya, kami tidak mempunyai cukup bukti untuk mengatakan bahwa perbedaan rata-rata antara kelompok yang kami bandingkan berbeda secara signifikan.

Hal ini menunjukkan bahwa varians sisa model ANOVA tinggi dibandingkan dengan variasi yang sebenarnya dapat dijelaskan oleh model tersebut.

Varians sisa dalam model regresi

Dalam model regresi, varians residu didefinisikan sebagai jumlah kuadrat selisih antara titik data yang diprediksi dan titik data yang diamati.

Ini dihitung sebagai berikut:

Σ(ŷ _saya – kamu _saya ) ²

Emas:

• Σ : simbol Yunani yang berarti “jumlah”
• ŷ _i : Titik data yang diprediksi
• y _i : Titik data yang diamati

Saat kita menyesuaikan model regresi, biasanya kita mendapatkan hasil seperti berikut:

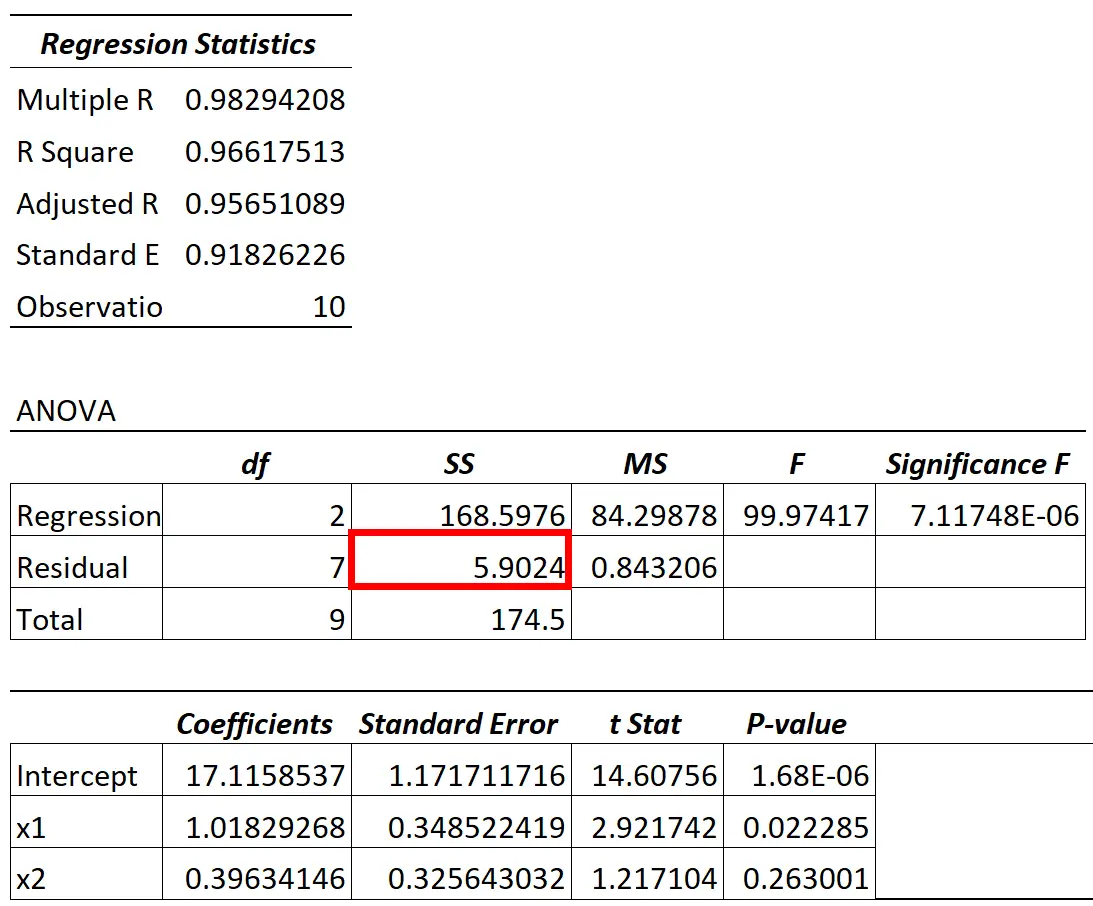
Nilai varians sisa dari model ANOVA dapat dilihat pada kolom SS (“jumlah kuadrat”) untuk variasi sisa.

Rasio variasi sisa terhadap variasi total dalam model menunjukkan persentase variasi variabel respon yang tidak dapat dijelaskan oleh variabel prediktor dalam model.

Misalnya, pada tabel di atas, kami menghitung persentasenya sebagai berikut:

• Variasi yang tidak dapat dijelaskan = Residu SS / Total SS
• Variasi yang tidak dapat dijelaskan = 5,9024 / 174,5
• Variasi yang tidak dapat dijelaskan = 0,0338

Nilai ini juga dapat dihitung menggunakan rumus berikut:

• Variasi yang tidak dapat dijelaskan = 1 – R ²
• Variasi yang tidak dapat dijelaskan = 1 – 0,96617
• Variasi yang tidak dapat dijelaskan = 0,0338

Nilai R-squared model menunjukkan persentase variasi variabel respon yang dapat dijelaskan oleh variabel prediktor.

Jadi, semakin rendah variasi yang tidak dapat dijelaskan, semakin mampu suatu model menggunakan variabel prediktor untuk menjelaskan variasi variabel respon.

Sumber daya tambahan

Berapa nilai R-kuadrat yang bagus?
Cara menghitung R-kuadrat di Excel
Cara menghitung R-kuadrat di R