Apakah variansnya bisa negatif?
Dalam statistik, istilah varians mengacu pada bagaimana nilai didistribusikan dalam kumpulan data tertentu.
Pertanyaan umum yang ditanyakan siswa tentang varians adalah:
Apakah variansnya bisa negatif?
Jawabannya: Tidak, variansnya tidak boleh negatif. Nilai terendah yang dapat diambil adalah nol.
Untuk memahami mengapa hal ini terjadi, kita perlu memahami bagaimana varians sebenarnya dihitung.
Cara menghitung kesenjangan
Rumus untuk mencari varians suatu sampel (dilambangkan s 2 ) adalah:
s 2 = Σ ( xi – x ) 2 / (n-1)
Emas:
- x : Maksud sampel
- x i : Pengamatan ke-i dalam sampel
- N : Ukuran sampel
- Σ : Simbol Yunani yang berarti “jumlah”
Misalnya, kita memiliki kumpulan data berikut dengan 10 nilai:
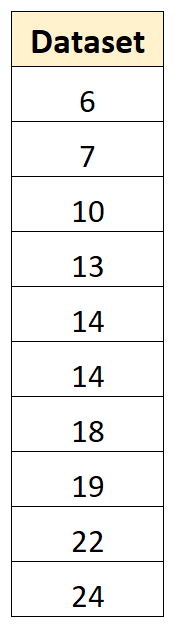
Kita dapat menggunakan langkah-langkah berikut untuk menghitung varians sampel ini:
Langkah 1: Temukan Rata-Ratanya
Rata-rata hanyalah rata-rata. Ini ternyata 14.7 .
Langkah 2: Temukan deviasi kuadrat
Kemudian kita dapat menghitung deviasi kuadrat masing-masing nilai dari mean.
Misalnya, deviasi kuadrat pertama dihitung sebagai (6-14.7) 2 = 75.69.
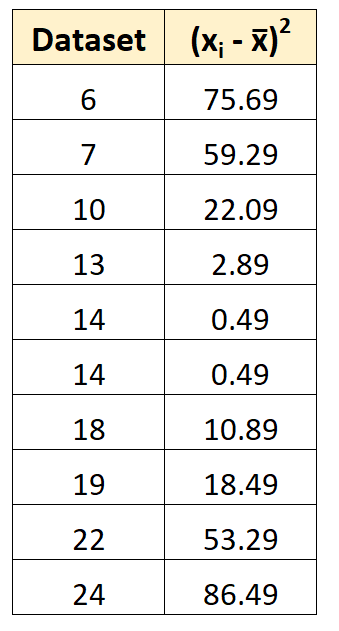
Langkah 3: Temukan jumlah simpangan kuadrat
Kemudian kita dapat menjumlahkan semua kuadrat simpangannya:
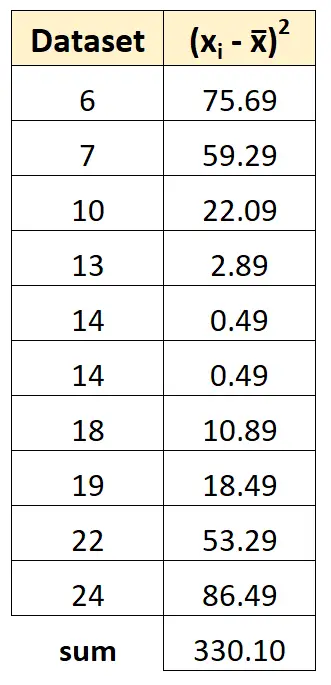
Langkah 4: Hitung varians sampel
Terakhir, kita dapat menghitung varians sampel sebagai jumlah deviasi kuadrat dibagi (n-1):
s 2 = 330,1 / (10-1) = 330,1 / 9 = 36,678
Varians sampelnya ternyata 36.678 .
Contoh varian nol
Satu-satunya cara agar suatu dataset memiliki varian nol adalah jika semua nilai dalam dataset tersebut sama .
Misalnya, kumpulan data berikut memiliki varian sampel nol:
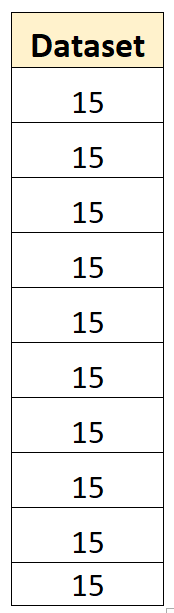
Rata-rata kumpulan data adalah 15 dan tidak ada satu pun nilai individual yang menyimpang dari rata-rata. Jadi, jumlah kuadrat deviasinya akan menjadi nol dan varians sampelnya akan menjadi nol.
Bisakah deviasi standar menjadi negatif?
Cara yang lebih umum untuk mengukur distribusi nilai dalam kumpulan data adalah dengan menggunakan deviasi standar, yang merupakan akar kuadrat dari varians.
Misalnya, jika varians suatu sampel adalah s2 = 36,678 , maka simpangan baku (ditulis s ) dihitung sebagai berikut:
s = √ s2 = √ 36,678 = 6,056
Karena kita telah mengetahui bahwa variansnya selalu nol atau bilangan positif, artinya simpangan baku tidak akan pernah negatif karena akar kuadrat dari nol atau bilangan positif tidak boleh negatif.
Sumber daya tambahan
Ukuran tendensi sentral: definisi dan contoh
Ukuran dispersi: definisi dan contoh
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya